Question Number 40814 by behi83417@gmail.com last updated on 27/Jul/18

Commented by MrW3 last updated on 27/Jul/18

$${x}=\mathrm{0},\:{y}=\mathrm{1} \\ $$$${or} \\ $$$${x}=\mathrm{1},\:{y}=\mathrm{0} \\ $$
Commented by math khazana by abdo last updated on 28/Jul/18
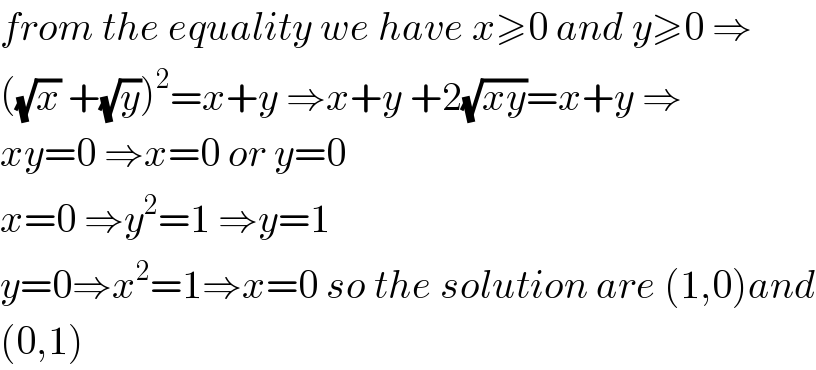
$${from}\:{the}\:{equality}\:{we}\:{have}\:{x}\geqslant\mathrm{0}\:{and}\:{y}\geqslant\mathrm{0}\:\Rightarrow \\ $$$$\left(\sqrt{{x}}\:+\sqrt{{y}}\right)^{\mathrm{2}} ={x}+{y}\:\Rightarrow{x}+{y}\:+\mathrm{2}\sqrt{{xy}}={x}+{y}\:\Rightarrow \\ $$$${xy}=\mathrm{0}\:\Rightarrow{x}=\mathrm{0}\:{or}\:{y}=\mathrm{0} \\ $$$${x}=\mathrm{0}\:\Rightarrow{y}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow{y}=\mathrm{1} \\ $$$${y}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}=\mathrm{0}\:{so}\:{the}\:{solution}\:{are}\:\left(\mathrm{1},\mathrm{0}\right){and} \\ $$$$\left(\mathrm{0},\mathrm{1}\right) \\ $$
Commented by behi83417@gmail.com last updated on 28/Jul/18
$${thank}\:{you}\:{both}\:{sirs}:{MrW}\mathrm{3}\:\&\:{mr}\:{abdo}. \\ $$
