Question Number 40822 by MrW3 last updated on 28/Jul/18

Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18
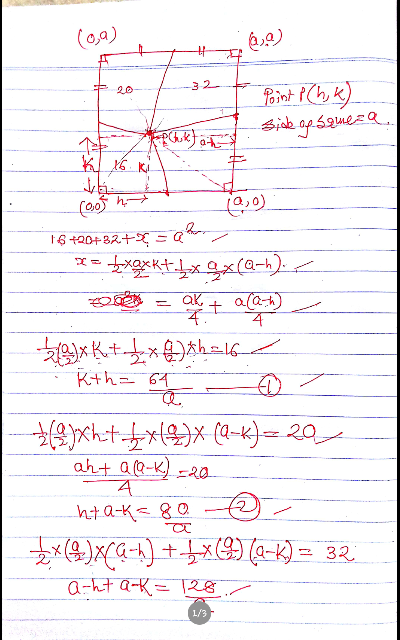
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18

Commented by MrW3 last updated on 28/Jul/18
$${answer}\:{is}\:{correct}\:{sir}! \\ $$$${thanks}! \\ $$
Answered by MrW3 last updated on 28/Jul/18
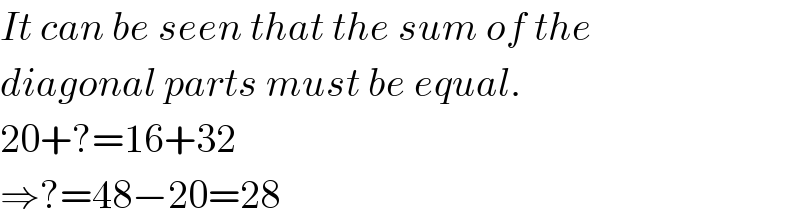
$${It}\:{can}\:{be}\:{seen}\:{that}\:{the}\:{sum}\:{of}\:{the} \\ $$$${diagonal}\:{parts}\:{must}\:{be}\:{equal}. \\ $$$$\mathrm{20}+?=\mathrm{16}+\mathrm{32} \\ $$$$\Rightarrow?=\mathrm{48}−\mathrm{20}=\mathrm{28} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18
$${pls}\:{say}\:{whether}\:{my}\:{answer}\:{is}\:{right}\:{or}\:{wrong} \\ $$$${method}\:{may}\:{be}\:{diffdrent}… \\ $$
Commented by MrW3 last updated on 28/Jul/18

Commented by MrW3 last updated on 28/Jul/18
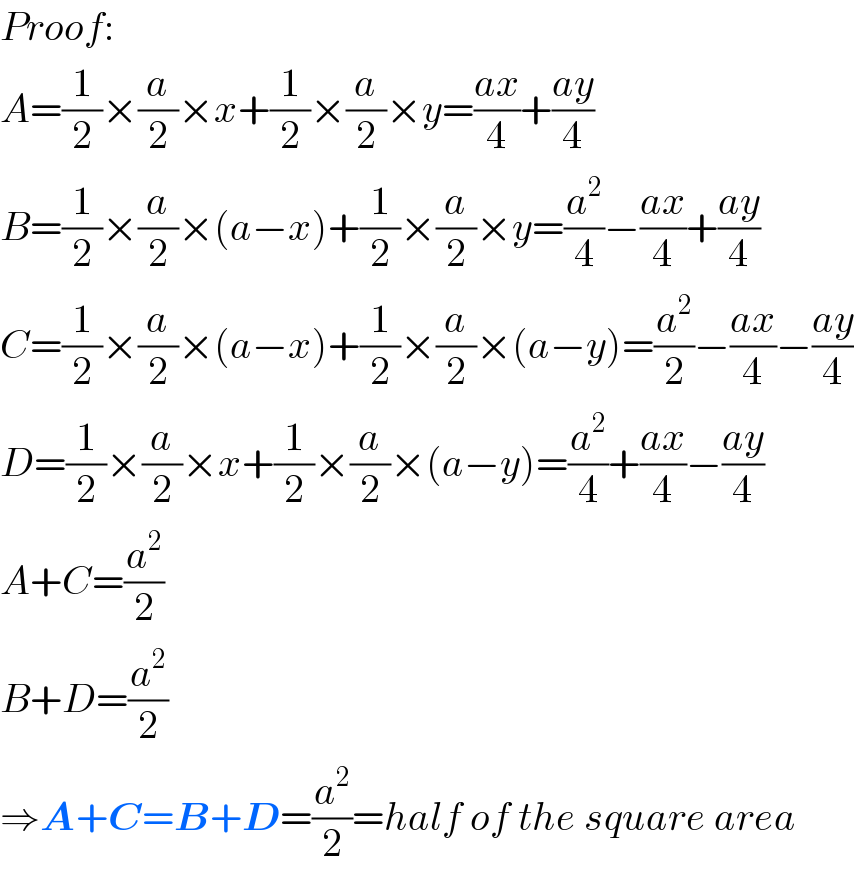
$${Proof}: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×{x}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×{y}=\frac{{ax}}{\mathrm{4}}+\frac{{ay}}{\mathrm{4}} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\left({a}−{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×{y}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{ax}}{\mathrm{4}}+\frac{{ay}}{\mathrm{4}} \\ $$$${C}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\left({a}−{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\left({a}−{y}\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{{ax}}{\mathrm{4}}−\frac{{ay}}{\mathrm{4}} \\ $$$${D}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×{x}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}×\left({a}−{y}\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{{ax}}{\mathrm{4}}−\frac{{ay}}{\mathrm{4}} \\ $$$${A}+{C}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${B}+{D}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{{A}}+\boldsymbol{{C}}=\boldsymbol{{B}}+\boldsymbol{{D}}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}={half}\:{of}\:{the}\:{square}\:{area} \\ $$
