Question-40826

Question Number 40826 by behi83417@gmail.com last updated on 28/Jul/18

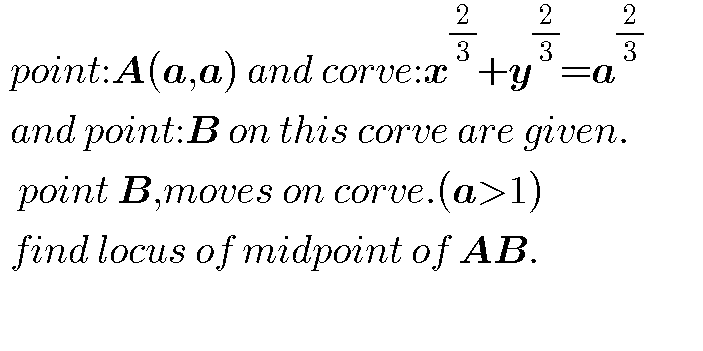
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18

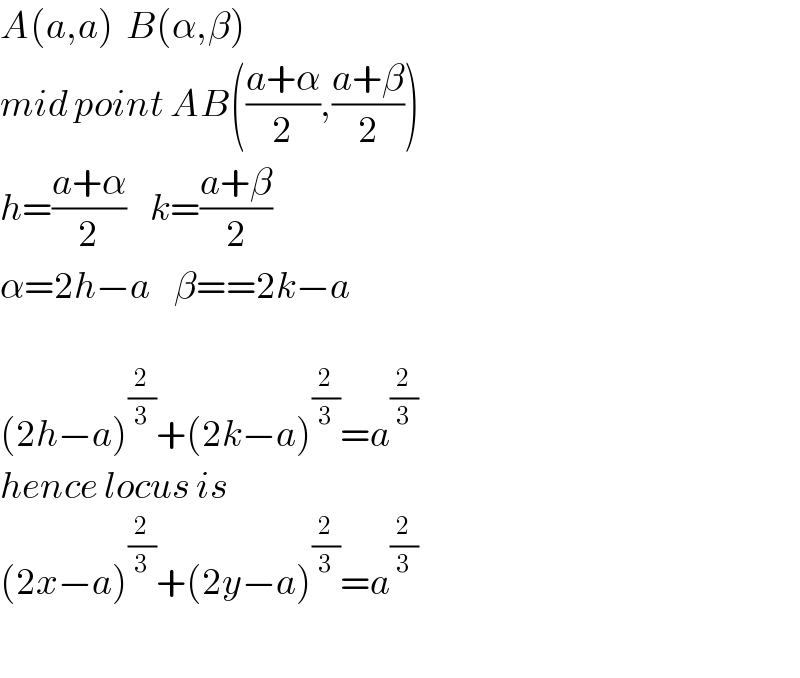
A(a,a) B(α,β) mid point AB(((a+α)/2),((a+β)/2)) h=((a+α)/2) k=((a+β)/2) α=2h−a β==2k−a (2h−a)^(2/3) +(2k−a)^(2/3) =a^(2/3) hence locus is (2x−a)^(2/3) +(2y−a)^(2/3) =a^(2/3)

$${A}\left({a},{a}\right)\:\:{B}\left(\alpha,\beta\right) \\ $$$${mid}\:{point}\:{AB}\left(\frac{{a}+\alpha}{\mathrm{2}},\frac{{a}+\beta}{\mathrm{2}}\right) \\ $$$${h}=\frac{{a}+\alpha}{\mathrm{2}}\:\:\:\:{k}=\frac{{a}+\beta}{\mathrm{2}} \\ $$$$\alpha=\mathrm{2}{h}−{a}\:\:\:\:\beta==\mathrm{2}{k}−{a} \\ $$$$ \\ $$$$\left(\mathrm{2}{h}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\mathrm{2}{k}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ={a}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${hence}\:{locus}\:{is} \\ $$$$\left(\mathrm{2}{x}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\mathrm{2}{y}−{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ={a}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 28/Jul/18

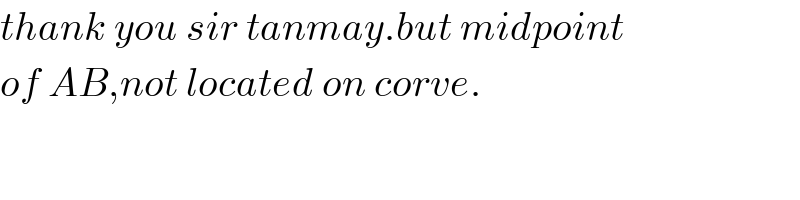
$${thank}\:{you}\:{sir}\:{tanmay}.{but}\:{midpoint} \\ $$$${of}\:{AB},{not}\:{located}\:{on}\:{corve}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 28/Jul/18

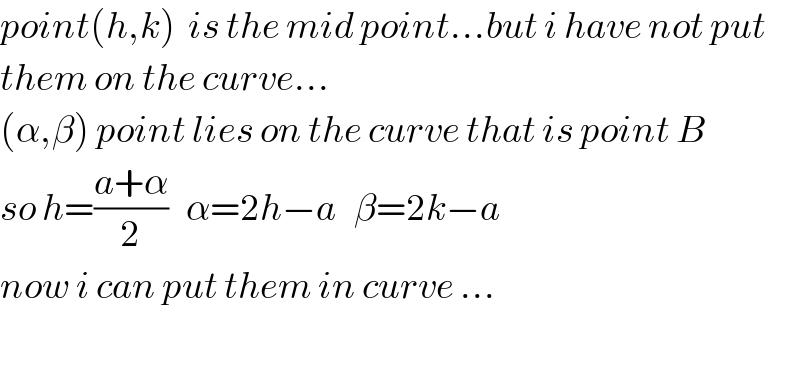
point(h,k) is the mid point...but i have not put them on the curve... (α,β) point lies on the curve that is point B so h=((a+α)/2) α=2h−a β=2k−a now i can put them in curve ...

$${point}\left({h},{k}\right)\:\:{is}\:{the}\:{mid}\:{point}…{but}\:{i}\:{have}\:{not}\:{put} \\ $$$${them}\:{on}\:{the}\:{curve}… \\ $$$$\left(\alpha,\beta\right)\:{point}\:{lies}\:{on}\:{the}\:{curve}\:{that}\:{is}\:{point}\:{B} \\ $$$${so}\:{h}=\frac{{a}+\alpha}{\mathrm{2}}\:\:\:\alpha=\mathrm{2}{h}−{a}\:\:\:\beta=\mathrm{2}{k}−{a} \\ $$$${now}\:{i}\:{can}\:{put}\:{them}\:{in}\:{curve}\:… \\ $$$$ \\ $$

Commented by behi83417@gmail.com last updated on 28/Jul/18

$${ok}.{thanks}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply