Question Number 40910 by rahul 19 last updated on 29/Jul/18

Answered by tanmay.chaudhury50@gmail.com last updated on 29/Jul/18
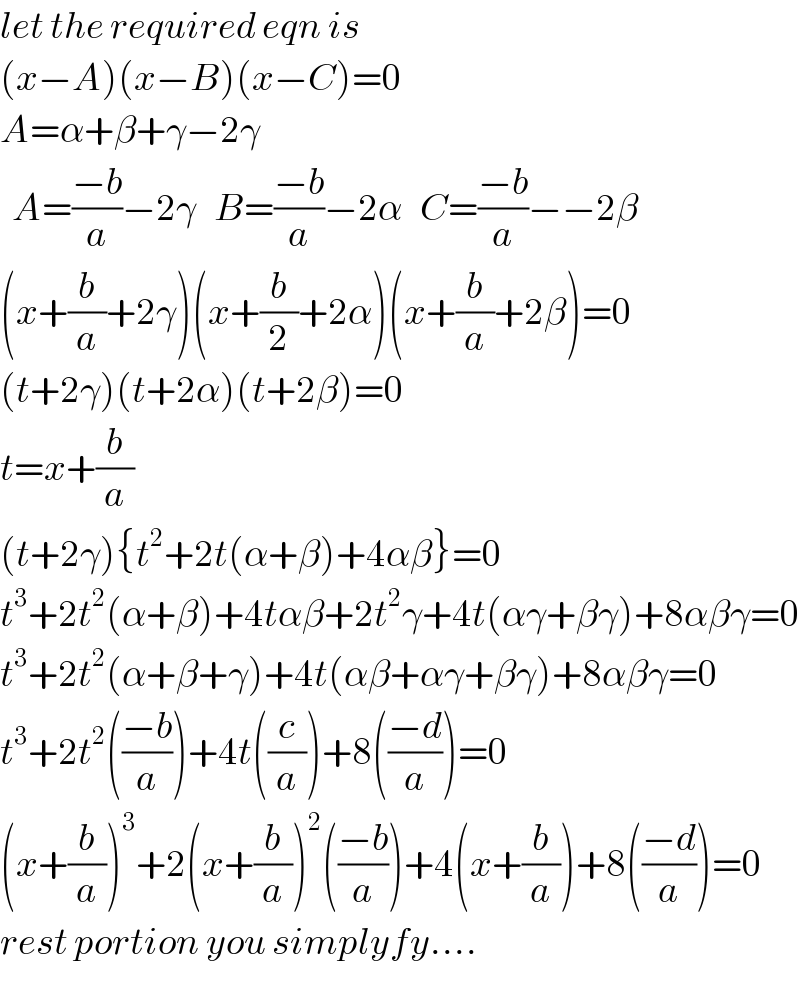
$${let}\:{the}\:{required}\:{eqn}\:{is} \\ $$$$\left({x}−{A}\right)\left({x}−{B}\right)\left({x}−{C}\right)=\mathrm{0} \\ $$$${A}=\alpha+\beta+\gamma−\mathrm{2}\gamma \\ $$$$\:\:{A}=\frac{−{b}}{{a}}−\mathrm{2}\gamma\:\:\:{B}=\frac{−{b}}{{a}}−\mathrm{2}\alpha\:\:\:{C}=\frac{−{b}}{{a}}−−\mathrm{2}\beta \\ $$$$\left({x}+\frac{{b}}{{a}}+\mathrm{2}\gamma\right)\left({x}+\frac{{b}}{\mathrm{2}}+\mathrm{2}\alpha\right)\left({x}+\frac{{b}}{{a}}+\mathrm{2}\beta\right)=\mathrm{0} \\ $$$$\left({t}+\mathrm{2}\gamma\right)\left({t}+\mathrm{2}\alpha\right)\left({t}+\mathrm{2}\beta\right)=\mathrm{0} \\ $$$${t}={x}+\frac{{b}}{{a}} \\ $$$$\left({t}+\mathrm{2}\gamma\right)\left\{{t}^{\mathrm{2}} +\mathrm{2}{t}\left(\alpha+\beta\right)+\mathrm{4}\alpha\beta\right\}=\mathrm{0} \\ $$$${t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} \left(\alpha+\beta\right)+\mathrm{4}{t}\alpha\beta+\mathrm{2}{t}^{\mathrm{2}} \gamma+\mathrm{4}{t}\left(\alpha\gamma+\beta\gamma\right)+\mathrm{8}\alpha\beta\gamma=\mathrm{0} \\ $$$${t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} \left(\alpha+\beta+\gamma\right)+\mathrm{4}{t}\left(\alpha\beta+\alpha\gamma+\beta\gamma\right)+\mathrm{8}\alpha\beta\gamma=\mathrm{0} \\ $$$${t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} \left(\frac{−{b}}{{a}}\right)+\mathrm{4}{t}\left(\frac{{c}}{{a}}\right)+\mathrm{8}\left(\frac{−{d}}{{a}}\right)=\mathrm{0} \\ $$$$\left({x}+\frac{{b}}{{a}}\right)^{\mathrm{3}} +\mathrm{2}\left({x}+\frac{{b}}{{a}}\right)^{\mathrm{2}} \left(\frac{−{b}}{{a}}\right)+\mathrm{4}\left({x}+\frac{{b}}{{a}}\right)+\mathrm{8}\left(\frac{−{d}}{{a}}\right)=\mathrm{0} \\ $$$${rest}\:{portion}\:{you}\:{simplyfy}…. \\ $$
Commented by rahul 19 last updated on 30/Jul/18

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
