Question Number 40917 by Tawa1 last updated on 29/Jul/18

Answered by tanmay.chaudhury50@gmail.com last updated on 30/Jul/18
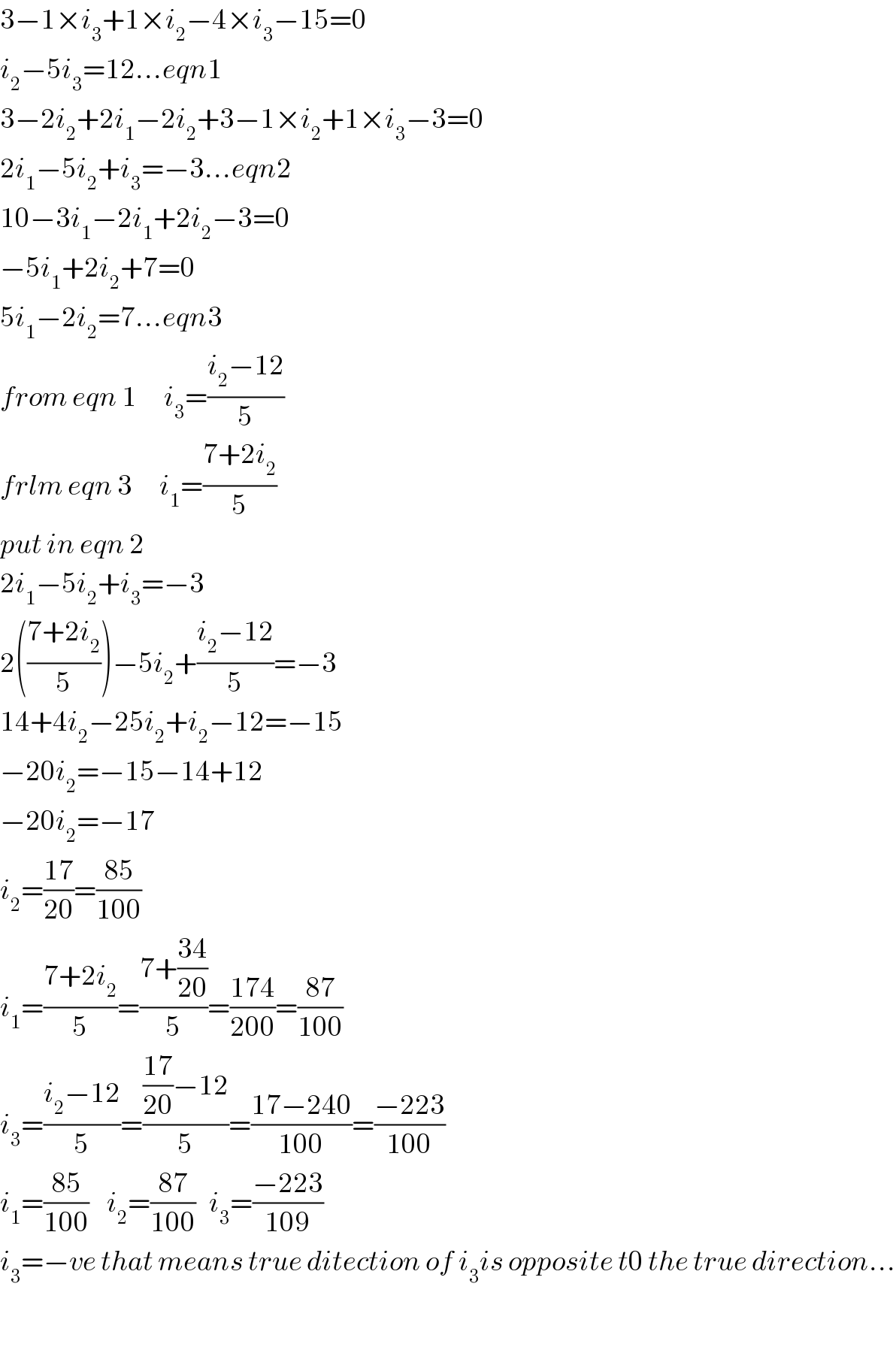
$$\mathrm{3}−\mathrm{1}×{i}_{\mathrm{3}} +\mathrm{1}×{i}_{\mathrm{2}} −\mathrm{4}×{i}_{\mathrm{3}} −\mathrm{15}=\mathrm{0} \\ $$$${i}_{\mathrm{2}} −\mathrm{5}{i}_{\mathrm{3}} =\mathrm{12}…{eqn}\mathrm{1} \\ $$$$\mathrm{3}−\mathrm{2}{i}_{\mathrm{2}} +\mathrm{2}{i}_{\mathrm{1}} −\mathrm{2}{i}_{\mathrm{2}} +\mathrm{3}−\mathrm{1}×{i}_{\mathrm{2}} +\mathrm{1}×{i}_{\mathrm{3}} −\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{i}_{\mathrm{1}} −\mathrm{5}{i}_{\mathrm{2}} +{i}_{\mathrm{3}} =−\mathrm{3}…{eqn}\mathrm{2} \\ $$$$\mathrm{10}−\mathrm{3}{i}_{\mathrm{1}} −\mathrm{2}{i}_{\mathrm{1}} +\mathrm{2}{i}_{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$$−\mathrm{5}{i}_{\mathrm{1}} +\mathrm{2}{i}_{\mathrm{2}} +\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{5}{i}_{\mathrm{1}} −\mathrm{2}{i}_{\mathrm{2}} =\mathrm{7}…{eqn}\mathrm{3} \\ $$$${from}\:{eqn}\:\mathrm{1}\:\:\:\:\:\:{i}_{\mathrm{3}} =\frac{{i}_{\mathrm{2}} −\mathrm{12}}{\mathrm{5}} \\ $$$${frlm}\:{eqn}\:\mathrm{3}\:\:\:\:\:\:{i}_{\mathrm{1}} =\frac{\mathrm{7}+\mathrm{2}{i}_{\mathrm{2}} }{\mathrm{5}} \\ $$$${put}\:{in}\:{eqn}\:\mathrm{2} \\ $$$$\mathrm{2}{i}_{\mathrm{1}} −\mathrm{5}{i}_{\mathrm{2}} +{i}_{\mathrm{3}} =−\mathrm{3} \\ $$$$\mathrm{2}\left(\frac{\mathrm{7}+\mathrm{2}{i}_{\mathrm{2}} }{\mathrm{5}}\right)−\mathrm{5}{i}_{\mathrm{2}} +\frac{{i}_{\mathrm{2}} −\mathrm{12}}{\mathrm{5}}=−\mathrm{3} \\ $$$$\mathrm{14}+\mathrm{4}{i}_{\mathrm{2}} −\mathrm{25}{i}_{\mathrm{2}} +{i}_{\mathrm{2}} −\mathrm{12}=−\mathrm{15} \\ $$$$−\mathrm{20}{i}_{\mathrm{2}} =−\mathrm{15}−\mathrm{14}+\mathrm{12} \\ $$$$−\mathrm{20}{i}_{\mathrm{2}} =−\mathrm{17} \\ $$$${i}_{\mathrm{2}} =\frac{\mathrm{17}}{\mathrm{20}}=\frac{\mathrm{85}}{\mathrm{100}} \\ $$$${i}_{\mathrm{1}} =\frac{\mathrm{7}+\mathrm{2}{i}_{\mathrm{2}} }{\mathrm{5}}=\frac{\mathrm{7}+\frac{\mathrm{34}}{\mathrm{20}}}{\mathrm{5}}=\frac{\mathrm{174}}{\mathrm{200}}=\frac{\mathrm{87}}{\mathrm{100}} \\ $$$${i}_{\mathrm{3}} =\frac{{i}_{\mathrm{2}} −\mathrm{12}}{\mathrm{5}}=\frac{\frac{\mathrm{17}}{\mathrm{20}}−\mathrm{12}}{\mathrm{5}}=\frac{\mathrm{17}−\mathrm{240}}{\mathrm{100}}=\frac{−\mathrm{223}}{\mathrm{100}} \\ $$$${i}_{\mathrm{1}} =\frac{\mathrm{85}}{\mathrm{100}}\:\:\:\:{i}_{\mathrm{2}} =\frac{\mathrm{87}}{\mathrm{100}}\:\:\:{i}_{\mathrm{3}} =\frac{−\mathrm{223}}{\mathrm{109}} \\ $$$${i}_{\mathrm{3}} =−{ve}\:{that}\:{means}\:{true}\:{ditection}\:{of}\:{i}_{\mathrm{3}} {is}\:{opposite}\:{t}\mathrm{0}\:{the}\:{true}\:{direction}… \\ $$$$ \\ $$
Commented by Tawa1 last updated on 30/Jul/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
