Question Number 40918 by Tawa1 last updated on 29/Jul/18

Answered by tanmay.chaudhury50@gmail.com last updated on 30/Jul/18
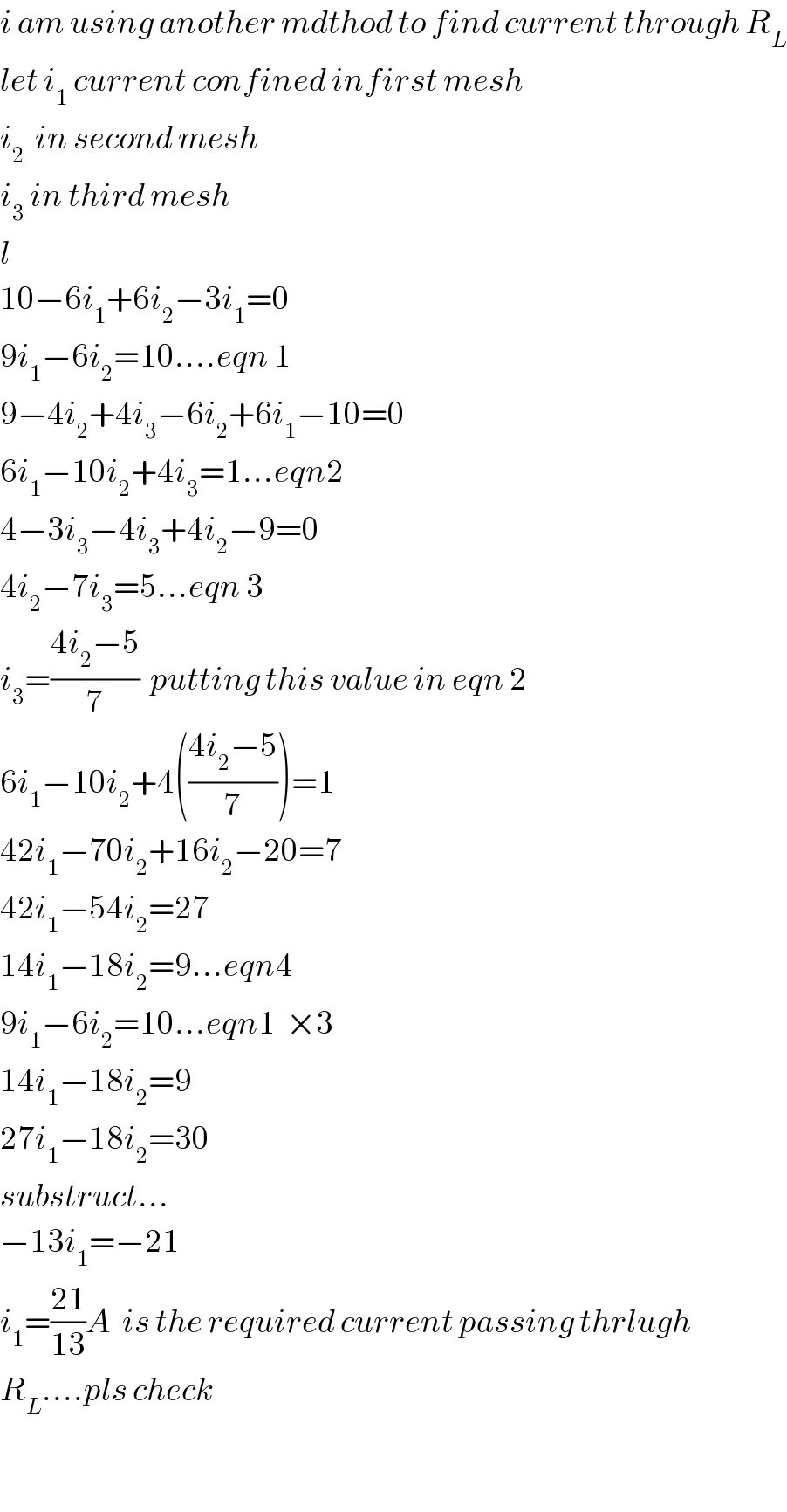
$${i}\:{am}\:{using}\:{another}\:{mdthod}\:{to}\:{find}\:{current}\:{through}\:{R}_{{L}} \\ $$$${let}\:{i}_{\mathrm{1}} \:{current}\:{confined}\:{infirst}\:{mesh} \\ $$$${i}_{\mathrm{2}} \:\:{in}\:{second}\:{mesh} \\ $$$${i}_{\mathrm{3}} \:{in}\:{third}\:{mesh} \\ $$$${l} \\ $$$$\mathrm{10}−\mathrm{6}{i}_{\mathrm{1}} +\mathrm{6}{i}_{\mathrm{2}} −\mathrm{3}{i}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{9}{i}_{\mathrm{1}} −\mathrm{6}{i}_{\mathrm{2}} =\mathrm{10}….{eqn}\:\mathrm{1} \\ $$$$\mathrm{9}−\mathrm{4}{i}_{\mathrm{2}} +\mathrm{4}{i}_{\mathrm{3}} −\mathrm{6}{i}_{\mathrm{2}} +\mathrm{6}{i}_{\mathrm{1}} −\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{6}{i}_{\mathrm{1}} −\mathrm{10}{i}_{\mathrm{2}} +\mathrm{4}{i}_{\mathrm{3}} =\mathrm{1}…{eqn}\mathrm{2} \\ $$$$\mathrm{4}−\mathrm{3}{i}_{\mathrm{3}} −\mathrm{4}{i}_{\mathrm{3}} +\mathrm{4}{i}_{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{4}{i}_{\mathrm{2}} −\mathrm{7}{i}_{\mathrm{3}} =\mathrm{5}…{eqn}\:\mathrm{3} \\ $$$${i}_{\mathrm{3}} =\frac{\mathrm{4}{i}_{\mathrm{2}} −\mathrm{5}}{\mathrm{7}}\:\:{putting}\:{this}\:{value}\:{in}\:{eqn}\:\mathrm{2} \\ $$$$\mathrm{6}{i}_{\mathrm{1}} −\mathrm{10}{i}_{\mathrm{2}} +\mathrm{4}\left(\frac{\mathrm{4}{i}_{\mathrm{2}} −\mathrm{5}}{\mathrm{7}}\right)=\mathrm{1} \\ $$$$\mathrm{42}{i}_{\mathrm{1}} −\mathrm{70}{i}_{\mathrm{2}} +\mathrm{16}{i}_{\mathrm{2}} −\mathrm{20}=\mathrm{7} \\ $$$$\mathrm{42}{i}_{\mathrm{1}} −\mathrm{54}{i}_{\mathrm{2}} =\mathrm{27} \\ $$$$\mathrm{14}{i}_{\mathrm{1}} −\mathrm{18}{i}_{\mathrm{2}} =\mathrm{9}…{eqn}\mathrm{4} \\ $$$$\mathrm{9}{i}_{\mathrm{1}} −\mathrm{6}{i}_{\mathrm{2}} =\mathrm{10}…{eqn}\mathrm{1}\:\:×\mathrm{3} \\ $$$$\mathrm{14}{i}_{\mathrm{1}} −\mathrm{18}{i}_{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{27}{i}_{\mathrm{1}} −\mathrm{18}{i}_{\mathrm{2}} =\mathrm{30} \\ $$$${substruct}… \\ $$$$−\mathrm{13}{i}_{\mathrm{1}} =−\mathrm{21} \\ $$$${i}_{\mathrm{1}} =\frac{\mathrm{21}}{\mathrm{13}}{A}\:\:{is}\:{the}\:{required}\:{current}\:{passing}\:{thrlugh} \\ $$$${R}_{{L}} ….{pls}\:{check} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 30/Jul/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{thanks}.\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Jul/18

$${thank}\:\:{you}\:{God}\:{shower}\:{its}\:{blessing}\:{to}\:{all}… \\ $$
