Question Number 41016 by Tawa1 last updated on 31/Jul/18
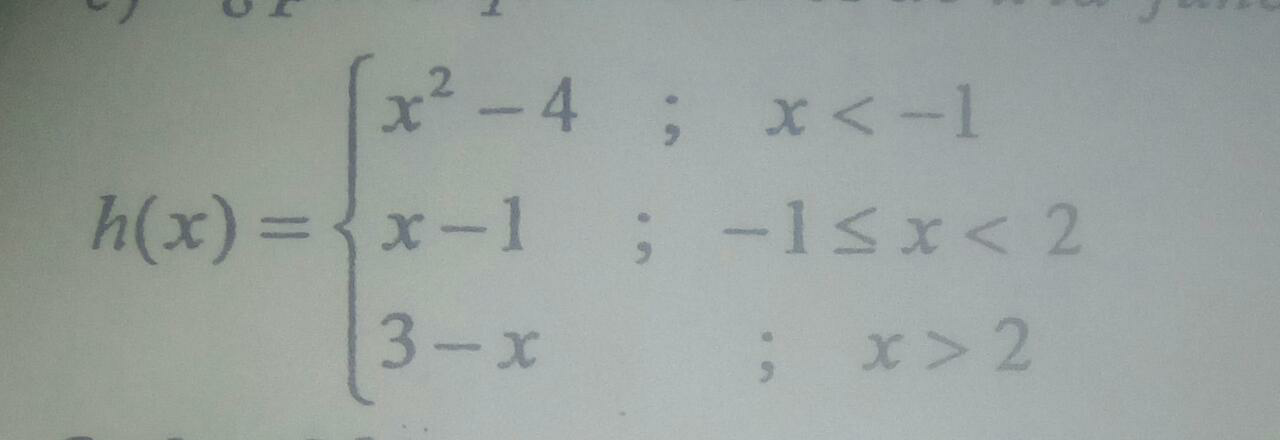
Commented by Tawa1 last updated on 31/Jul/18

$$\mathrm{For}\:\mathrm{what}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{is}\:\mathrm{the}\:\mathrm{function}\:\mathrm{h}\left(\mathrm{x}\right)\:\mathrm{discontinuous}\:\mathrm{and}\:\mathrm{do}\:\mathrm{we} \\ $$$$\mathrm{call}\:\mathrm{functions}\:\mathrm{like}\:\mathrm{the}\:\mathrm{question}\:\mathrm{above}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 31/Jul/18

$${a}\:{function}\:{h}\left({x}\right)\:{will}\:{be}\:{continuous}\:{at}\:{x}={a} \\ $$$${if} \\ $$$$\underset{{x}\rightarrow{a}−} {\mathrm{lim}}\:{h}\left({x}\right)=\underset{{x}\rightarrow{a}+} {\mathrm{lim}}{h}\left({x}\right)={h}\left({a}\right) \\ $$$${let}\:{test}\:{at}\:{x}=−\mathrm{1} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}−} {\mathrm{lim}}\:{x}^{\mathrm{2}} −\mathrm{4}=−\mathrm{3} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}+} {\mathrm{lim}}\:{x}−\mathrm{1}=−\mathrm{2} \\ $$$${h}\left(−\mathrm{1}\right)=−\mathrm{2} \\ $$$${so}\:{at}\:{x}=−\mathrm{1}\:{h}\left({x}\right)\:\:{is}\:{discontinuous} \\ $$$${let}\:{test}\:{at}\:{x}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{2}−} {\mathrm{lim}}\:{x}−\mathrm{1}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{2}+} {\mathrm{lim}}\:\mathrm{3}−{x}=\mathrm{1} \\ $$$${but}\:{h}\left(\mathrm{2}\right)\:{can}\:{not}\:{be}\:{determined}\:{so}\:{continuty} \\ $$$${test}\:{at}\:{x}=\mathrm{2}\:{can}\:{not}\:{be}\:{done}… \\ $$$${but}\:{h}\left({x}\right)\:{is}\:{discontinuous}\:{at}\:{x}=−\mathrm{1} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 31/Jul/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 31/Jul/18
$${thank}\:{you}…{same}\:{to}\:{you}… \\ $$
