Question Number 41027 by behi83417@gmail.com last updated on 31/Jul/18
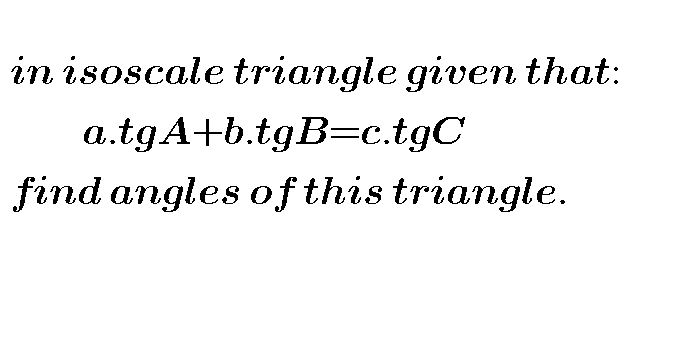
Answered by MJS last updated on 01/Aug/18
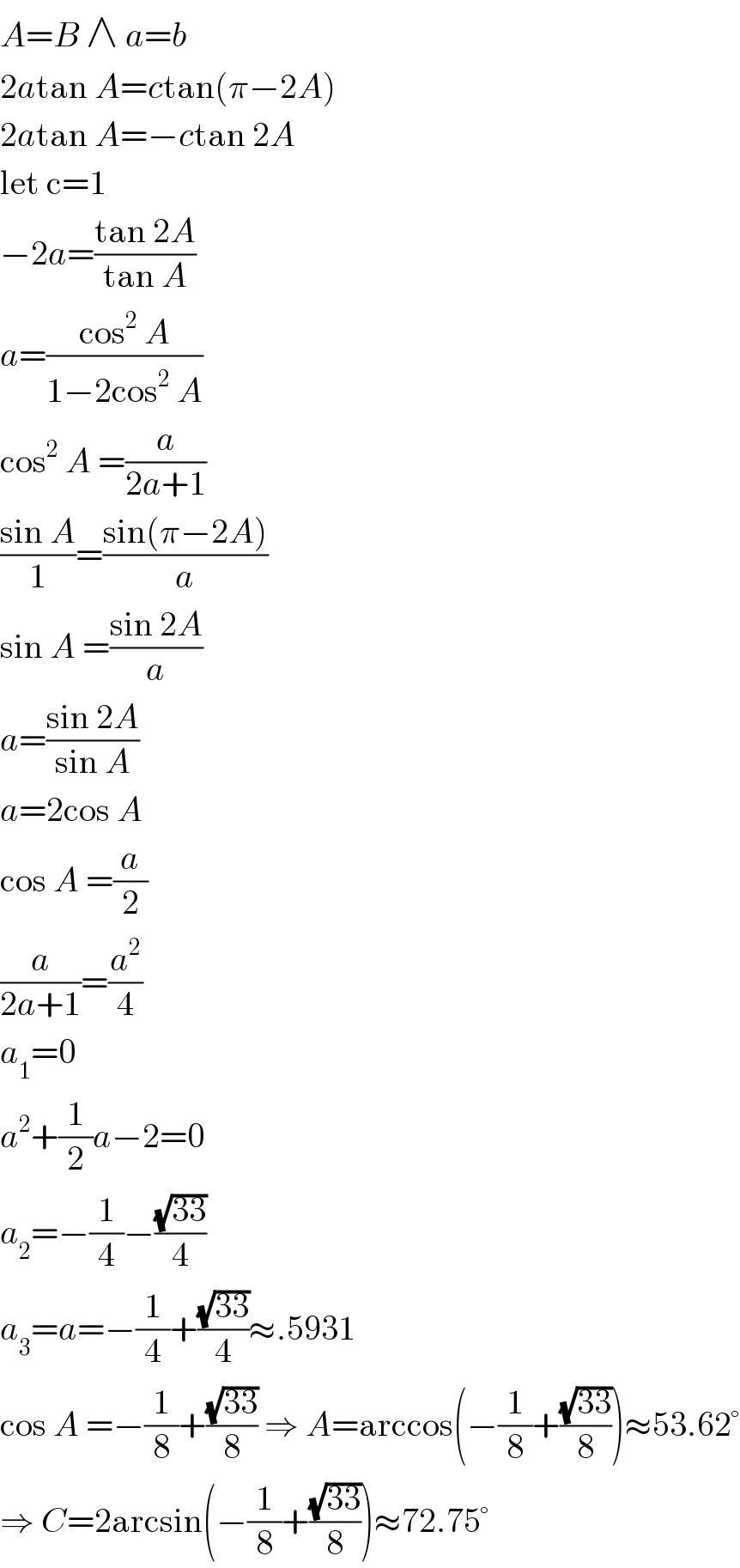
$${A}={B}\:\wedge\:{a}={b} \\ $$$$\mathrm{2}{a}\mathrm{tan}\:{A}={c}\mathrm{tan}\left(\pi−\mathrm{2}{A}\right) \\ $$$$\mathrm{2}{a}\mathrm{tan}\:{A}=−{c}\mathrm{tan}\:\mathrm{2}{A} \\ $$$$\mathrm{let}\:\mathrm{c}=\mathrm{1} \\ $$$$−\mathrm{2}{a}=\frac{\mathrm{tan}\:\mathrm{2}{A}}{\mathrm{tan}\:{A}} \\ $$$${a}=\frac{\mathrm{cos}^{\mathrm{2}} \:{A}}{\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \:{A}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{A}\:=\frac{{a}}{\mathrm{2}{a}+\mathrm{1}} \\ $$$$\frac{\mathrm{sin}\:{A}}{\mathrm{1}}=\frac{\mathrm{sin}\left(\pi−\mathrm{2}{A}\right)}{{a}} \\ $$$$\mathrm{sin}\:{A}\:=\frac{\mathrm{sin}\:\mathrm{2}{A}}{{a}} \\ $$$${a}=\frac{\mathrm{sin}\:\mathrm{2}{A}}{\mathrm{sin}\:{A}} \\ $$$${a}=\mathrm{2cos}\:{A} \\ $$$$\mathrm{cos}\:{A}\:=\frac{{a}}{\mathrm{2}} \\ $$$$\frac{{a}}{\mathrm{2}{a}+\mathrm{1}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${a}_{\mathrm{1}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{a}−\mathrm{2}=\mathrm{0} \\ $$$${a}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\sqrt{\mathrm{33}}}{\mathrm{4}} \\ $$$${a}_{\mathrm{3}} ={a}=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{4}}\approx.\mathrm{5931} \\ $$$$\mathrm{cos}\:{A}\:=−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{8}}\:\Rightarrow\:{A}=\mathrm{arccos}\left(−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{8}}\right)\approx\mathrm{53}.\mathrm{62}° \\ $$$$\Rightarrow\:{C}=\mathrm{2arcsin}\left(−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{8}}\right)\approx\mathrm{72}.\mathrm{75}° \\ $$
