Menu Close

Question-41157

Tinku Tara 0 Comments
Pin




Question Number 41157 by ajfour last updated on 02/Aug/18
Commented by ajfour last updated on 02/Aug/18
If arc length is constant, equal to l, and segment area a maximum, find the radius.
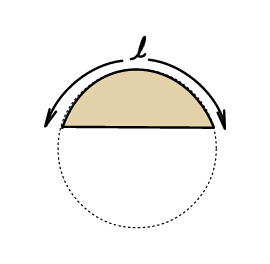
$${If}\:{arc}\:{length}\:{is}\:{constant},\:{equal} \\ $$$${to}\:\boldsymbol{{l}},\:{and}\:{segment}\:{area}\:{a}\:{maximum}, \\ $$$${find}\:{the}\:{radius}. \\ $$
Commented by MJS last updated on 02/Aug/18
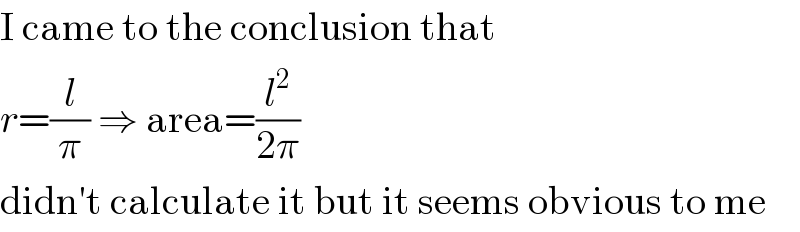
I came to the conclusion that r=(l/π) ⇒ area=(l^2 /(2π)) didn′t calculate it but it seems obvious to me
$$\mathrm{I}\:\mathrm{came}\:\mathrm{to}\:\mathrm{the}\:\mathrm{conclusion}\:\mathrm{that} \\ $$$${r}=\frac{{l}}{\pi}\:\Rightarrow\:\mathrm{area}=\frac{{l}^{\mathrm{2}} }{\mathrm{2}\pi} \\ $$$$\mathrm{didn}'\mathrm{t}\:\mathrm{calculate}\:\mathrm{it}\:\mathrm{but}\:\mathrm{it}\:\mathrm{seems}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me} \\ $$
Commented by ajfour last updated on 03/Aug/18
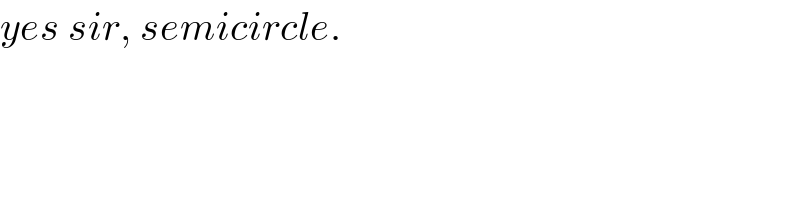
yes sir, semicircle.
$${yes}\:{sir},\:{semicircle}. \\ $$
Answered by MrW3 last updated on 02/Aug/18
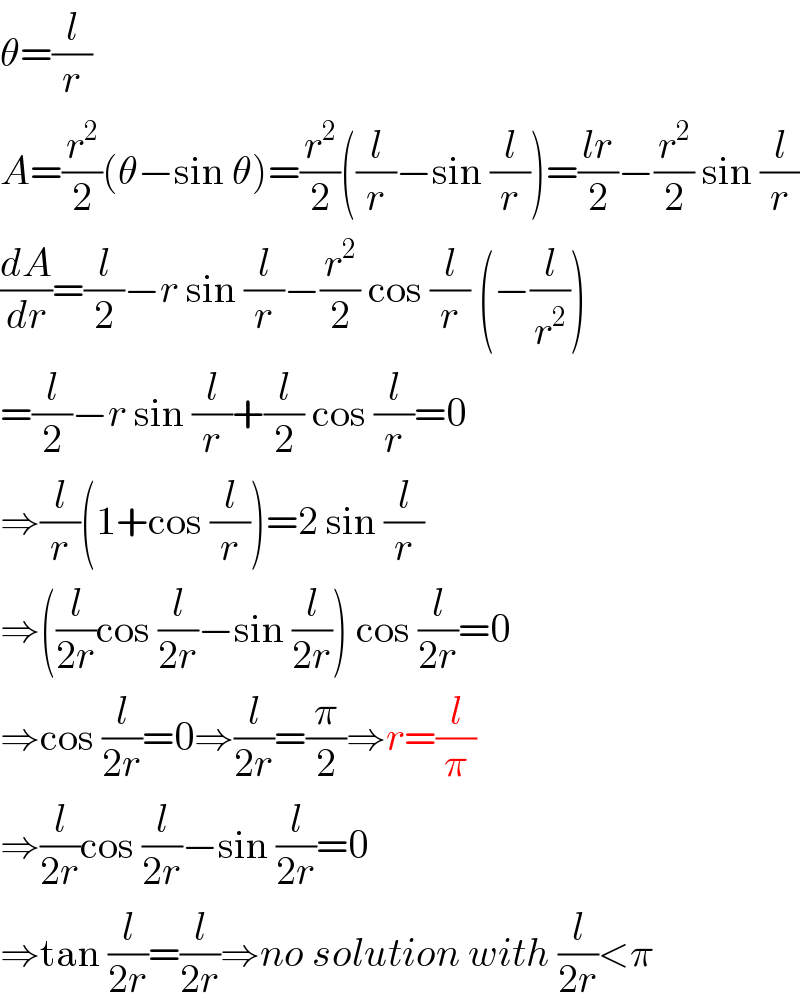
θ=(l/r) A=(r^2 /2)(θ−sin θ)=(r^2 /2)((l/r)−sin (l/r))=((lr)/2)−(r^2 /2) sin (l/r) (dA/dr)=(l/2)−r sin (l/r)−(r^2 /2) cos (l/r) (−(l/r^2 )) =(l/2)−r sin (l/r)+(l/2) cos (l/r)=0 ⇒(l/r)(1+cos (l/r))=2 sin (l/r) ⇒((l/(2r))cos (l/(2r))−sin (l/(2r))) cos (l/(2r))=0 ⇒cos (l/(2r))=0⇒(l/(2r))=(π/2)⇒r=(l/π) ⇒(l/(2r))cos (l/(2r))−sin (l/(2r))=0 ⇒tan (l/(2r))=(l/(2r))⇒no solution with (l/(2r))<π
$$\theta=\frac{{l}}{{r}} \\ $$$${A}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{{l}}{{r}}−\mathrm{sin}\:\frac{{l}}{{r}}\right)=\frac{{lr}}{\mathrm{2}}−\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{sin}\:\frac{{l}}{{r}} \\ $$$$\frac{{dA}}{{dr}}=\frac{{l}}{\mathrm{2}}−{r}\:\mathrm{sin}\:\frac{{l}}{{r}}−\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{cos}\:\frac{{l}}{{r}}\:\left(−\frac{{l}}{{r}^{\mathrm{2}} }\right) \\ $$$$=\frac{{l}}{\mathrm{2}}−{r}\:\mathrm{sin}\:\frac{{l}}{{r}}+\frac{{l}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{l}}{{r}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{l}}{{r}}\left(\mathrm{1}+\mathrm{cos}\:\frac{{l}}{{r}}\right)=\mathrm{2}\:\mathrm{sin}\:\frac{{l}}{{r}} \\ $$$$\Rightarrow\left(\frac{{l}}{\mathrm{2}{r}}\mathrm{cos}\:\frac{{l}}{\mathrm{2}{r}}−\mathrm{sin}\:\frac{{l}}{\mathrm{2}{r}}\right)\:\mathrm{cos}\:\frac{{l}}{\mathrm{2}{r}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{{l}}{\mathrm{2}{r}}=\mathrm{0}\Rightarrow\frac{{l}}{\mathrm{2}{r}}=\frac{\pi}{\mathrm{2}}\Rightarrow{r}=\frac{{l}}{\pi} \\ $$$$\Rightarrow\frac{{l}}{\mathrm{2}{r}}\mathrm{cos}\:\frac{{l}}{\mathrm{2}{r}}−\mathrm{sin}\:\frac{{l}}{\mathrm{2}{r}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{{l}}{\mathrm{2}{r}}=\frac{{l}}{\mathrm{2}{r}}\Rightarrow{no}\:{solution}\:{with}\:\frac{{l}}{\mathrm{2}{r}}<\pi \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
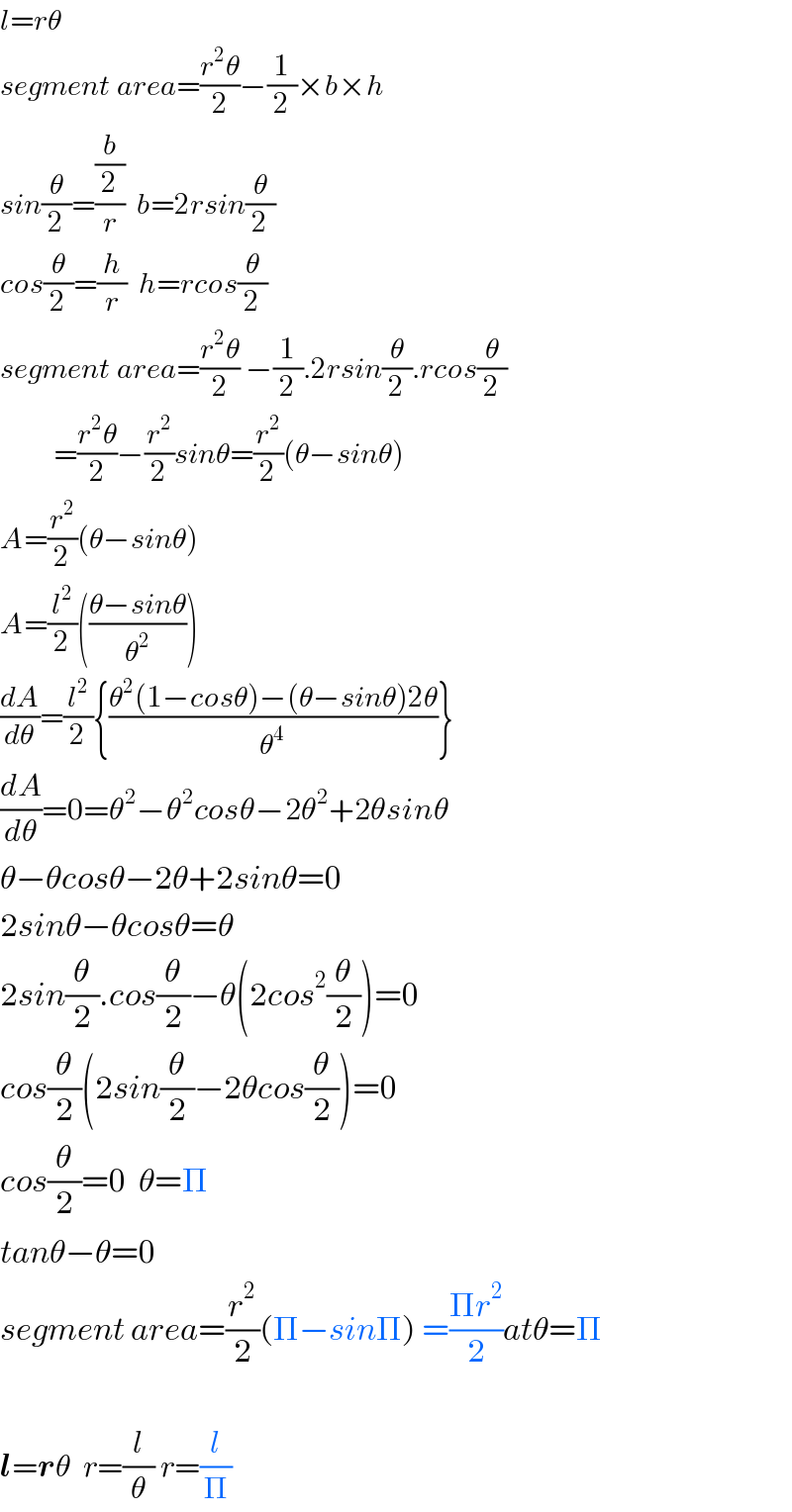
l=rθ segment area=((r^2 θ)/2)−(1/2)×b×h sin(θ/2)=((b/2)/r) b=2rsin(θ/2) cos(θ/2)=(h/r) h=rcos(θ/2) segment area=((r^2 θ)/2) −(1/2).2rsin(θ/2).rcos(θ/2) =((r^2 θ)/2)−(r^2 /2)sinθ=(r^2 /2)(θ−sinθ) A=(r^2 /2)(θ−sinθ) A=(l^2 /2)(((θ−sinθ)/θ^2 )) (dA/dθ)=(l^2 /2){((θ^2 (1−cosθ)−(θ−sinθ)2θ)/θ^4 )} (dA/dθ)=0=θ^2 −θ^2 cosθ−2θ^2 +2θsinθ θ−θcosθ−2θ+2sinθ=0 2sinθ−θcosθ=θ 2sin(θ/2).cos(θ/2)−θ(2cos^2 (θ/2))=0 cos(θ/2)(2sin(θ/2)−2θcos(θ/2))=0 cos(θ/2)=0 θ=Π tanθ−θ=0 segment area=(r^2 /2)(Π−sinΠ) =((Πr^2 )/2)atθ=Π l=rθ r=(l/θ) r=(l/Π)
$${l}={r}\theta \\ $$$${segment}\:{area}=\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}×{b}×{h} \\ $$$${sin}\frac{\theta}{\mathrm{2}}=\frac{\frac{{b}}{\mathrm{2}}}{{r}}\:\:{b}=\mathrm{2}{rsin}\frac{\theta}{\mathrm{2}} \\ $$$${cos}\frac{\theta}{\mathrm{2}}=\frac{{h}}{{r}}\:\:{h}={rcos}\frac{\theta}{\mathrm{2}} \\ $$$${segment}\:{area}=\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{rsin}\frac{\theta}{\mathrm{2}}.{rcos}\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}}−\frac{{r}^{\mathrm{2}} }{\mathrm{2}}{sin}\theta=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−{sin}\theta\right) \\ $$$${A}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−{sin}\theta\right) \\ $$$${A}=\frac{{l}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\theta−{sin}\theta}{\theta^{\mathrm{2}} }\right) \\ $$$$\frac{{dA}}{{d}\theta}=\frac{{l}^{\mathrm{2}} }{\mathrm{2}}\left\{\frac{\theta^{\mathrm{2}} \left(\mathrm{1}−{cos}\theta\right)−\left(\theta−{sin}\theta\right)\mathrm{2}\theta}{\theta^{\mathrm{4}} }\right\} \\ $$$$\frac{{dA}}{{d}\theta}=\mathrm{0}=\theta^{\mathrm{2}} −\theta^{\mathrm{2}} {cos}\theta−\mathrm{2}\theta^{\mathrm{2}} +\mathrm{2}\theta{sin}\theta \\ $$$$\theta−\theta{cos}\theta−\mathrm{2}\theta+\mathrm{2}{sin}\theta=\mathrm{0} \\ $$$$\mathrm{2}{sin}\theta−\theta{cos}\theta=\theta \\ $$$$\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}.{cos}\frac{\theta}{\mathrm{2}}−\theta\left(\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${cos}\frac{\theta}{\mathrm{2}}\left(\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}−\mathrm{2}\theta{cos}\frac{\theta}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${cos}\frac{\theta}{\mathrm{2}}=\mathrm{0}\:\:\theta=\Pi \\ $$$${tan}\theta−\theta=\mathrm{0} \\ $$$${segment}\:{area}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\Pi−{sin}\Pi\right)\:=\frac{\Pi{r}^{\mathrm{2}} }{\mathrm{2}}{at}\theta=\Pi \\ $$$$ \\ $$$$\boldsymbol{{l}}=\boldsymbol{{r}}\theta\:\:{r}=\frac{{l}}{\theta}\:{r}=\frac{{l}}{\Pi} \\ $$
Commented by behi83417@gmail.com last updated on 03/Aug/18
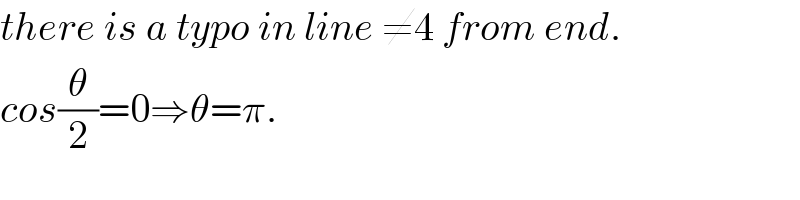
there is a typo in line ≠4 from end. cos(θ/2)=0⇒θ=π.
$${there}\:{is}\:{a}\:{typo}\:{in}\:{line}\:\neq\mathrm{4}\:{from}\:{end}. \\ $$$${cos}\frac{\theta}{\mathrm{2}}=\mathrm{0}\Rightarrow\theta=\pi. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
yes true...let me rectify...
$${yes}\:{true}…{let}\:{me}\:{rectify}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *