Question Number 41203 by ajfour last updated on 03/Aug/18
Commented by ajfour last updated on 03/Aug/18

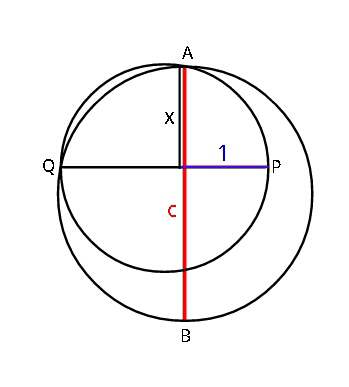
$${If}\:{AB}=\:{c}\:{is}\:{a}\:{diameter}\:{of}\:{larger} \\ $$$${circle}\:{and}\:{PQ}\:{is}\:{a}\:{diameter}\:{of} \\ $$$${the}\:{smaller}\:{circle},\:{find}\:\boldsymbol{\mathrm{x}}\:{in}\:{terms} \\ $$$${of}\:{c}\:;\:\left({geometrically}\:\right). \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
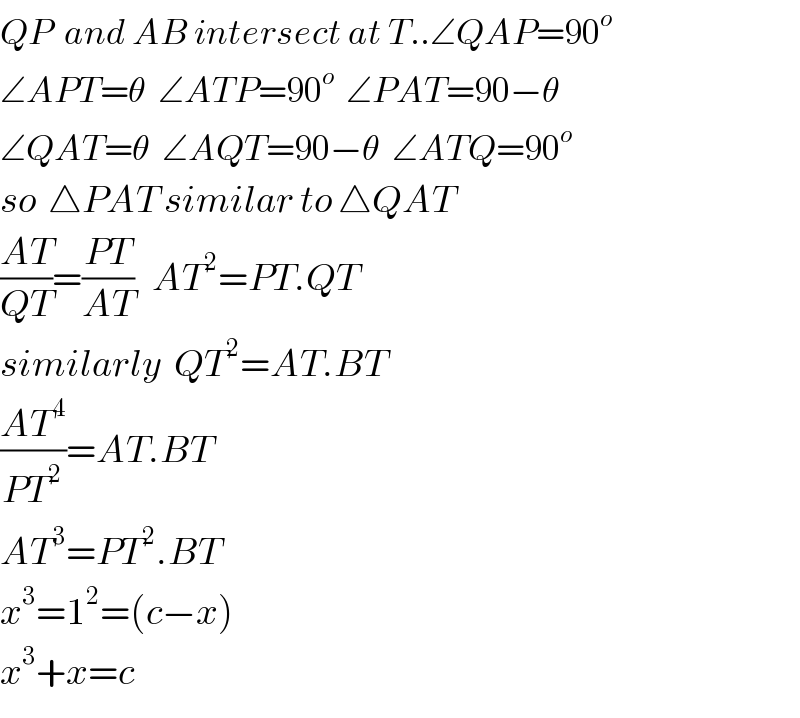
$${QP}\:\:{and}\:{AB}\:{intersect}\:{at}\:{T}..\angle{QAP}=\mathrm{90}^{{o}} \\ $$$$\angle{APT}=\theta\:\:\angle{ATP}=\mathrm{90}^{{o}} \:\:\angle{PAT}=\mathrm{90}−\theta \\ $$$$\angle{QAT}=\theta\:\:\angle{AQT}=\mathrm{90}−\theta\:\:\angle{ATQ}=\mathrm{90}^{{o}} \\ $$$${so}\:\:\bigtriangleup{PAT}\:{similar}\:{to}\:\bigtriangleup{QAT} \\ $$$$\frac{{AT}}{{QT}}=\frac{{PT}}{{AT}}\:\:\:{AT}^{\mathrm{2}} ={PT}.{QT} \\ $$$${similarly}\:\:{QT}^{\mathrm{2}} ={AT}.{BT} \\ $$$$\frac{{AT}^{\mathrm{4}} }{{PT}^{\mathrm{2}} }={AT}.{BT} \\ $$$${AT}^{\mathrm{3}} ={PT}^{\mathrm{2}} .{BT} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}^{\mathrm{2}} =\left({c}−{x}\right) \\ $$$${x}^{\mathrm{3}} +{x}={c} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18

$${why}\:{you}\:{ignore}\:{my}\:{answer}…{no}\:{comment} \\ $$$${whether}\:{answer}\:{got}\:{conform}\:{to}\:{the}\:{answer} \\ $$$${given}\:{in}\:{the}\:{source}\:{from}\:{where}\:{you}\:{posted}\:{the} \\ $$$${question}… \\ $$
Commented by ajfour last updated on 03/Aug/18

$${i}\:{seek}\:{an}\:{alternate}\:{solution}\:{not} \\ $$$${using}\:{any}\:{algebraic}\:{technique} \\ $$$${like}\:{cardano}'{s} \\ $$$${through}\:{construction}\:{i}\:{seek}\:{to} \\ $$$${obtain}\:{x}\:{in}\:{terms}\:{of}\:{c}.\:{please}\:{try}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
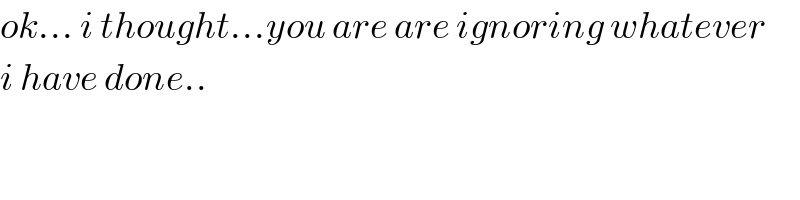
$${ok}…\:{i}\:{thought}…{you}\:{are}\:{are}\:{ignoring}\:{whatever} \\ $$$${i}\:{have}\:{done}.. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18

$${let}\:{QP}\:{and}\:{AB}\:{intersect}\:{at}\:{point}\:{T} \\ $$$${AT}^{\mathrm{2}} ={QT}.{TP} \\ $$$${QT}^{\mathrm{2}} ={AT}.{BT} \\ $$$$\frac{{AT}^{\mathrm{4}} }{{TP}^{\mathrm{2}} }={AT}.{BT} \\ $$$${AT}^{\mathrm{3}} ={TP}^{\mathrm{2}} .{BT} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}^{\mathrm{2}} .\left({c}−{x}\right) \\ $$$${x}^{\mathrm{3}} +{x}={c} \\ $$
