Menu Close

Question-41214

Tinku Tara 0 Comments
Pin




Question Number 41214 by ajfour last updated on 03/Aug/18
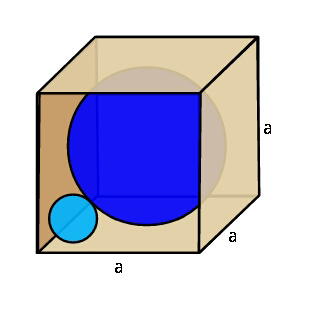
Commented by ajfour last updated on 03/Aug/18
Larger sphere is inscribed in the cube; while the smaller sphere is tangent to three faces of cube and to the larger sphere. Find its radius.
$${Larger}\:{sphere}\:{is}\:{inscribed}\:{in}\:{the} \\ $$$${cube};\:{while}\:{the}\:{smaller}\:{sphere} \\ $$$${is}\:{tangent}\:{to}\:{three}\:{faces}\:{of}\:{cube} \\ $$$${and}\:{to}\:{the}\:{larger}\:{sphere}.\:{Find}\:{its} \\ $$$${radius}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
2R=a radius of big sphere r=radius of small sphere small sphere touch three plane ...so distance from centre of small sphere to the plane is the radius eqn of small (x−r)^2 +(y−r)^2 +(z−r)^2 =r^2 eqn big sphere (x−(a/2))^2 +(y−(a/2))^2 +(z−(a/2))^2 =((a/2))^2 distance between the centre of two sphere is sum of the radius ((a/2)−r)^2 +((a/2)−r)^2 +((a/2)−r)^2 =(r+(a/2))^2 3((a^2 /4)−ar+r^2 )=r^2 +ar+(a^2 /4) ((3a^2 )/4)−3ar+3r^2 −r^2 −ar−(a^2 /4)=0 (a^2 /2)−4ar+2r^2 =0 4r^2 −8ar+a^2 =0 r=((8a±(√(64a^2 −4.4.a^2 )))/8) r=((8a±(√(48a^2 )))/8) r=((8a±4(√3) a)/8) r=a±((√3)/2)a pls check... t
$$\mathrm{2}{R}={a}\:\:{radius}\:{of}\:{big}\:{sphere} \\ $$$${r}={radius}\:{of}\:{small}\:{sphere} \\ $$$${small}\:{sphere}\:{touch}\:{three}\:{plane}\:…{so}\:{distance} \\ $$$${from}\:{centre}\:{of}\:{small}\:{sphere}\:{to}\:{the}\:{plane}\:{is}\:{the} \\ $$$${radius} \\ $$$${eqn}\:{of}\:{small}\:\left({x}−{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} +\left({z}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\:{eqn}\:{big}\:{sphere} \\ $$$$\left({x}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({z}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${distance}\:{between}\:\:{the}\:{centre}\:{of}\:{two}\:{sphere} \\ $$$${is}\:{sum}\:{of}\:{the}\:{radius} \\ $$$$\left(\frac{{a}}{\mathrm{2}}−{r}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}−{r}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}−{r}\right)^{\mathrm{2}} =\left({r}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−{ar}+{r}^{\mathrm{2}} \right)={r}^{\mathrm{2}} +{ar}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{3}{ar}+\mathrm{3}{r}^{\mathrm{2}} −{r}^{\mathrm{2}} −{ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{4}{ar}+\mathrm{2}{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{r}^{\mathrm{2}} −\mathrm{8}{ar}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${r}=\frac{\mathrm{8}{a}\pm\sqrt{\mathrm{64}{a}^{\mathrm{2}} −\mathrm{4}.\mathrm{4}.{a}^{\mathrm{2}} }}{\mathrm{8}} \\ $$$${r}=\frac{\mathrm{8}{a}\pm\sqrt{\mathrm{48}{a}^{\mathrm{2}} }}{\mathrm{8}} \\ $$$${r}=\frac{\mathrm{8}{a}\pm\mathrm{4}\sqrt{\mathrm{3}}\:{a}}{\mathrm{8}} \\ $$$${r}={a}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}\:\:\:{pls}\:{check}… \\ $$$${t} \\ $$
Commented by MJS last updated on 03/Aug/18
not sure but I think sphere 1 with r=a(1−((√3)/2)) is the searched one sphere 2 with r=a(1+((√3)/2)) is touching the given big sphere from above you “ask” for spheres touching the given sphere plus the 3 planes, so the answer is 2 spheres.
$$\mathrm{not}\:\mathrm{sure}\:\mathrm{but}\:\mathrm{I}\:\mathrm{think} \\ $$$$\mathrm{sphere}\:\mathrm{1}\:\mathrm{with}\:{r}={a}\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{searched}\:\mathrm{one} \\ $$$$\mathrm{sphere}\:\mathrm{2}\:\mathrm{with}\:{r}={a}\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\mathrm{is}\:\mathrm{touching}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{big}\:\mathrm{sphere}\:\mathrm{from}\:\mathrm{above} \\ $$$$\mathrm{you}\:“\mathrm{ask}''\:\mathrm{for}\:\mathrm{spheres}\:\mathrm{touching}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{sphere}\:\mathrm{plus}\:\mathrm{the}\:\mathrm{3}\:\mathrm{planes},\:\mathrm{so}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is} \\ $$$$\mathrm{2}\:\mathrm{spheres}. \\ $$
Commented by ajfour last updated on 03/Aug/18
thank you Tanmay Sir; i couldnot follow the answer with the r=(a/2)(1+(√3)) initially, clear now!
$${thank}\:{you}\:{Tanmay}\:{Sir};\:{i}\:{couldnot}\:{follow} \\ $$$${the}\:{answer}\:{with}\:{the}\:{r}=\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$${initially},\:{clear}\:{now}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Aug/18
i solve prlblem in details so that other can understand...and also able to find mistake if any...so i do not apply short cut method.... by the way thank you and thaks to MJS sir for going through my post...
$${i}\:{solve}\:{prlblem}\:{in}\:{details}\:{so}\:{that}\:{other}\:{can}\: \\ $$$${understand}…{and}\:{also}\:{able}\:{to}\:{find}\:{mistake}\: \\ $$$${if}\:{any}…{so}\:{i}\:{do}\:{not}\:{apply}\:{short}\:{cut}\:{method}…. \\ $$$${by}\:{the}\:{way}\:\:{thank}\:{you}\:{and}\:\:{thaks}\:{to}\:{MJS}\:{sir}\: \\ $$$${for}\:{going}\:{through}\:{my}\:{post}… \\ $$$$ \\ $$
Answered by ajfour last updated on 03/Aug/18
r(√3)+r+R+R(√3) = a(√3) ⇒ r= ((a(√3)−R(1+(√3)))/(1+(√3))) and as R=a/2 we have r=((a(√3)−((a(√3))/2)−(a/2))/(1+(√3))) = ((a((√3)−1))/(2((√3)+1))) or r= (a/2)(2−(√3)) .
$${r}\sqrt{\mathrm{3}}+{r}+{R}+{R}\sqrt{\mathrm{3}}\:=\:{a}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:{r}=\:\frac{{a}\sqrt{\mathrm{3}}−{R}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}{\mathrm{1}+\sqrt{\mathrm{3}}} \\ $$$${and}\:{as}\:{R}={a}/\mathrm{2}\:\:{we}\:{have} \\ $$$$\:\:\:{r}=\frac{{a}\sqrt{\mathrm{3}}−\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{3}}}\:=\:\frac{{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)} \\ $$$${or}\:\:\:\:\:\boldsymbol{{r}}=\:\frac{\boldsymbol{{a}}}{\mathrm{2}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\:. \\ $$
Answered by MrW3 last updated on 04/Aug/18
distance of corner of cube to center of small sphere: (√3) r distance of corner of cube to center of big sphere: (√3) R distance of center of small sphere to that of big sphere: (√3) R−(√3) r=r+R ⇒r=((R((√3)−1))/( (√3)+1))=((a((√3)−1))/(2((√3)+1)))=((a(2−(√3)))/2)
$${distance}\:{of}\:{corner}\:{of}\:{cube}\:{to}\:{center}\:{of}\:{small}\:{sphere}: \\ $$$$\sqrt{\mathrm{3}}\:{r} \\ $$$${distance}\:{of}\:{corner}\:{of}\:{cube}\:{to}\:{center}\:{of}\:{big}\:{sphere}: \\ $$$$\sqrt{\mathrm{3}}\:{R} \\ $$$${distance}\:{of}\:{center}\:{of}\:{small}\:{sphere}\:{to}\:{that}\:{of}\:{big}\:{sphere}: \\ $$$$\sqrt{\mathrm{3}}\:{R}−\sqrt{\mathrm{3}}\:{r}={r}+{R} \\ $$$$\Rightarrow{r}=\frac{{R}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{3}}+\mathrm{1}}=\frac{{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}=\frac{{a}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *