Question Number 41233 by ajfour last updated on 03/Aug/18
Commented by ajfour last updated on 03/Aug/18
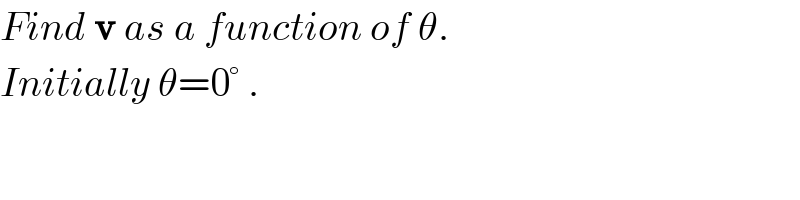
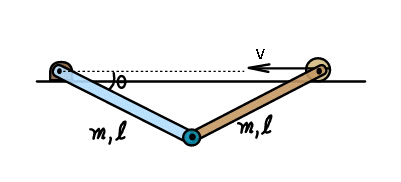
$${Find}\:\boldsymbol{\mathrm{v}}\:{as}\:{a}\:{function}\:{of}\:\theta. \\ $$$${Initially}\:\theta=\mathrm{0}°\:. \\ $$
Answered by MrW3 last updated on 04/Aug/18
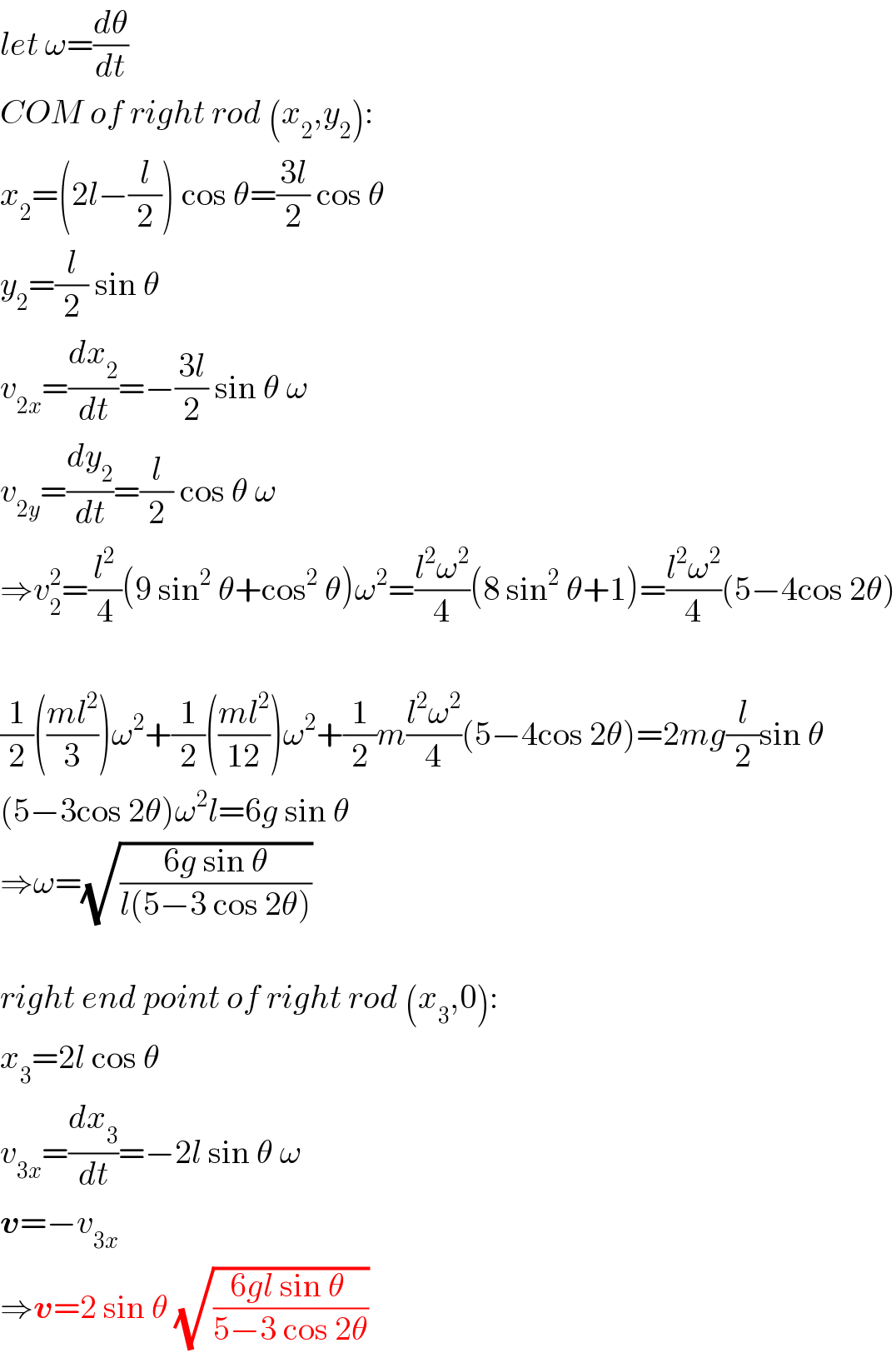
$${let}\:\omega=\frac{{d}\theta}{{dt}} \\ $$$${COM}\:{of}\:{right}\:{rod}\:\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right): \\ $$$${x}_{\mathrm{2}} =\left(\mathrm{2}{l}−\frac{{l}}{\mathrm{2}}\right)\:\mathrm{cos}\:\theta=\frac{\mathrm{3}{l}}{\mathrm{2}}\:\mathrm{cos}\:\theta \\ $$$${y}_{\mathrm{2}} =\frac{{l}}{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${v}_{\mathrm{2}{x}} =\frac{{dx}_{\mathrm{2}} }{{dt}}=−\frac{\mathrm{3}{l}}{\mathrm{2}}\:\mathrm{sin}\:\theta\:\omega \\ $$$${v}_{\mathrm{2}{y}} =\frac{{dy}_{\mathrm{2}} }{{dt}}=\frac{{l}}{\mathrm{2}}\:\mathrm{cos}\:\theta\:\omega \\ $$$$\Rightarrow{v}_{\mathrm{2}} ^{\mathrm{2}} =\frac{{l}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{9}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta\right)\omega^{\mathrm{2}} =\frac{{l}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{1}\right)=\frac{{l}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{5}−\mathrm{4cos}\:\mathrm{2}\theta\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right)\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}\right)\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{m}\frac{{l}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{5}−\mathrm{4cos}\:\mathrm{2}\theta\right)=\mathrm{2}{mg}\frac{{l}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$$\left(\mathrm{5}−\mathrm{3cos}\:\mathrm{2}\theta\right)\omega^{\mathrm{2}} {l}=\mathrm{6}{g}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{6}{g}\:\mathrm{sin}\:\theta}{{l}\left(\mathrm{5}−\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta\right)}} \\ $$$$ \\ $$$${right}\:{end}\:{point}\:{of}\:{right}\:{rod}\:\left({x}_{\mathrm{3}} ,\mathrm{0}\right): \\ $$$${x}_{\mathrm{3}} =\mathrm{2}{l}\:\mathrm{cos}\:\theta \\ $$$${v}_{\mathrm{3}{x}} =\frac{{dx}_{\mathrm{3}} }{{dt}}=−\mathrm{2}{l}\:\mathrm{sin}\:\theta\:\omega \\ $$$$\boldsymbol{{v}}=−{v}_{\mathrm{3}{x}} \\ $$$$\Rightarrow\boldsymbol{{v}}=\mathrm{2}\:\mathrm{sin}\:\theta\:\sqrt{\frac{\mathrm{6}{gl}\:\mathrm{sin}\:\theta\:}{\mathrm{5}−\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta}} \\ $$
Commented by ajfour last updated on 04/Aug/18
$${Excellent}\:{Sir},\:{thanks}\:{a}\:{lot}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18

$${excellent}… \\ $$
Commented by MrW3 last updated on 04/Aug/18

$${thank}\:{you}\:{both}! \\ $$
Answered by MrW3 last updated on 05/Aug/18

Commented by MrW3 last updated on 06/Aug/18
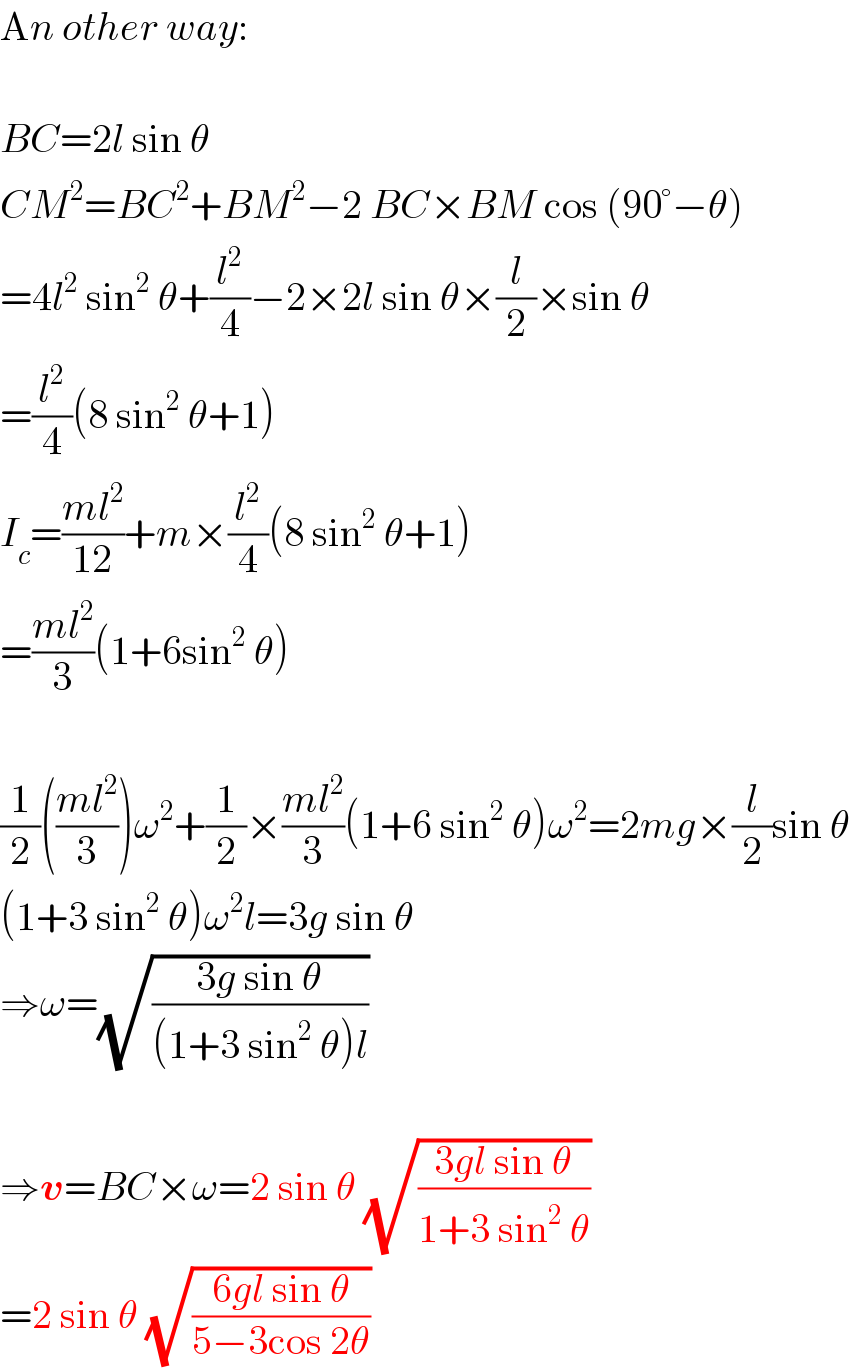
$$\mathrm{A}{n}\:{other}\:{way}: \\ $$$$ \\ $$$${BC}=\mathrm{2}{l}\:\mathrm{sin}\:\theta \\ $$$${CM}^{\mathrm{2}} ={BC}^{\mathrm{2}} +{BM}^{\mathrm{2}} −\mathrm{2}\:{BC}×{BM}\:\mathrm{cos}\:\left(\mathrm{90}°−\theta\right) \\ $$$$=\mathrm{4}{l}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta+\frac{{l}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}×\mathrm{2}{l}\:\mathrm{sin}\:\theta×\frac{{l}}{\mathrm{2}}×\mathrm{sin}\:\theta \\ $$$$=\frac{{l}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{1}\right) \\ $$$${I}_{{c}} =\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}+{m}×\frac{{l}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{1}\right) \\ $$$$=\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{1}+\mathrm{6sin}^{\mathrm{2}} \:\theta\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\right)\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{{ml}^{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{1}+\mathrm{6}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)\omega^{\mathrm{2}} =\mathrm{2}{mg}×\frac{{l}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$$\left(\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)\omega^{\mathrm{2}} {l}=\mathrm{3}{g}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{3}{g}\:\mathrm{sin}\:\theta}{\left(\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right){l}}} \\ $$$$ \\ $$$$\Rightarrow\boldsymbol{{v}}={BC}×\omega=\mathrm{2}\:\mathrm{sin}\:\theta\:\sqrt{\frac{\mathrm{3}{gl}\:\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$=\mathrm{2}\:\mathrm{sin}\:\theta\:\sqrt{\frac{\mathrm{6}{gl}\:\mathrm{sin}\:\theta}{\mathrm{5}−\mathrm{3cos}\:\mathrm{2}\theta}} \\ $$
