Menu Close

Question-41246

Tinku Tara 0 Comments
Pin




Question Number 41246 by Raj Singh last updated on 04/Aug/18
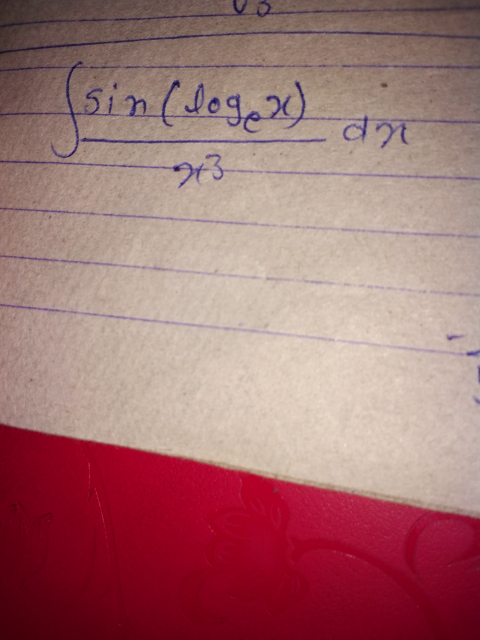
Commented by prof Abdo imad last updated on 04/Aug/18
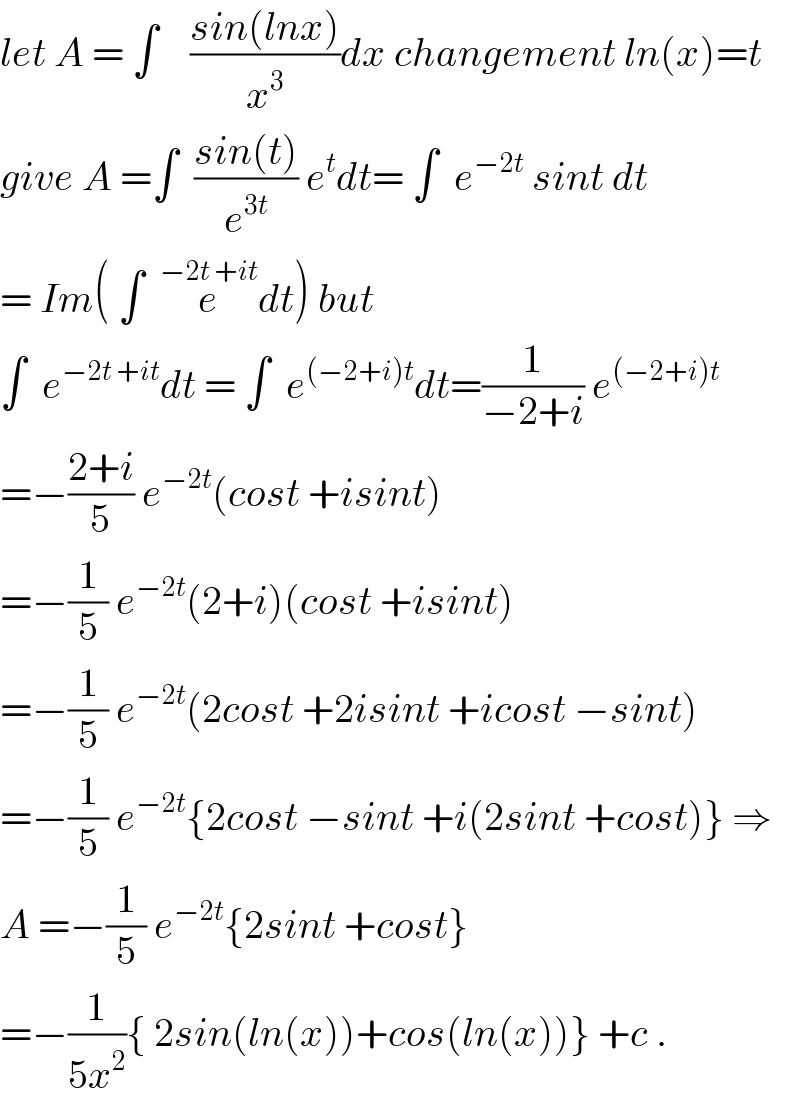
let A = ∫ ((sin(lnx))/x^3 )dx changement ln(x)=t give A =∫ ((sin(t))/e^(3t) ) e^t dt= ∫ e^(−2t) sint dt = Im( ∫ e^(−2t +it) dt) but ∫ e^(−2t +it) dt = ∫ e^((−2+i)t) dt=(1/(−2+i)) e^((−2+i)t) =−((2+i)/5) e^(−2t) (cost +isint) =−(1/5) e^(−2t) (2+i)(cost +isint) =−(1/5) e^(−2t) (2cost +2isint +icost −sint) =−(1/5) e^(−2t) {2cost −sint +i(2sint +cost)} ⇒ A =−(1/5) e^(−2t) {2sint +cost} =−(1/(5x^2 )){ 2sin(ln(x))+cos(ln(x))} +c .
$${let}\:{A}\:=\:\int\:\:\:\:\frac{{sin}\left({lnx}\right)}{{x}^{\mathrm{3}} }{dx}\:{changement}\:{ln}\left({x}\right)={t} \\ $$$${give}\:{A}\:=\int\:\:\frac{{sin}\left({t}\right)}{{e}^{\mathrm{3}{t}} }\:{e}^{{t}} {dt}=\:\int\:\:{e}^{−\mathrm{2}{t}} \:{sint}\:{dt} \\ $$$$=\:{Im}\left(\:\int\:\:\overset{−\mathrm{2}{t}\:+{it}} {{e}dt}\right)\:{but} \\ $$$$\int\:\:{e}^{−\mathrm{2}{t}\:+{it}} {dt}\:=\:\int\:\:{e}^{\left(−\mathrm{2}+{i}\right){t}} {dt}=\frac{\mathrm{1}}{−\mathrm{2}+{i}}\:{e}^{\left(−\mathrm{2}+{i}\right){t}} \: \\ $$$$=−\frac{\mathrm{2}+{i}}{\mathrm{5}}\:{e}^{−\mathrm{2}{t}} \left({cost}\:+{isint}\right)\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\:{e}^{−\mathrm{2}{t}} \left(\mathrm{2}+{i}\right)\left({cost}\:+{isint}\right)\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\:{e}^{−\mathrm{2}{t}} \left(\mathrm{2}{cost}\:+\mathrm{2}{isint}\:+{icost}\:−{sint}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\:{e}^{−\mathrm{2}{t}} \left\{\mathrm{2}{cost}\:−{sint}\:+{i}\left(\mathrm{2}{sint}\:+{cost}\right)\right\}\:\Rightarrow \\ $$$${A}\:=−\frac{\mathrm{1}}{\mathrm{5}}\:{e}^{−\mathrm{2}{t}} \left\{\mathrm{2}{sint}\:+{cost}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}{x}^{\mathrm{2}} }\left\{\:\mathrm{2}{sin}\left({ln}\left({x}\right)\right)+{cos}\left({ln}\left({x}\right)\right)\right\}\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18
t=lnx (dt/dx)=(1/x) x=e^t ∫((sint)/e^(3t) )×e^t dt ∫e^(−2t) sintdt p=∫e^(−2t) cost dt q=∫e^(−2t) sint dt p+ia=∫e^(−2t) e^(it) dt p+iq=∫e^(−2t) (cost+isint)dt=∫e^(−2t) .e^(it) dt ∫e^((−2+i)t) dt=(e^((−2+i)t) /((−2+i)))+c =e^(−2t) .(((−2−i)(e^(it) ))/((−2)^2 −(i)^2 ))+c =e^(−2t) .(((−2−i)(cost+isint))/(4+1)) =e^(−2t) .(((−2cost−i2sint−icost−i^2 sint))/5) =e^(−2t.) (((−2cost+sint)−i(2sint+cost))/5) separating real and imaginary part =e^(−2t) .(((−2cost+sint))/5)+i ((e^(−2t) (−2sint−cost))/5) so ∫e^(−2t) sint dt=e^(−2t) .(((−2sint−cost))/5) =x^(−2) .(((−2sinlnx−coslnx))/5) pls check...
$${t}={lnx}\:\:\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{x}}\:\: \\ $$$${x}={e}^{{t}} \\ $$$$\int\frac{{sint}}{{e}^{\mathrm{3}{t}} }×{e}^{{t}} {dt} \\ $$$$\int{e}^{−\mathrm{2}{t}} {sintdt} \\ $$$${p}=\int{e}^{−\mathrm{2}{t}} {cost}\:{dt} \\ $$$${q}=\int{e}^{−\mathrm{2}{t}} {sint}\:{dt} \\ $$$${p}+{ia}=\int{e}^{−\mathrm{2}{t}} {e}^{{it}} \:{dt} \\ $$$${p}+{iq}=\int{e}^{−\mathrm{2}{t}} \left({cost}+{isint}\right){dt}=\int{e}^{−\mathrm{2}{t}} .{e}^{{it}} \:{dt} \\ $$$$\int{e}^{\left(−\mathrm{2}+{i}\right){t}} {dt}=\frac{{e}^{\left(−\mathrm{2}+{i}\right){t}} }{\left(−\mathrm{2}+{i}\right)}+{c} \\ $$$$={e}^{−\mathrm{2}{t}} .\frac{\left(−\mathrm{2}−{i}\right)\left({e}^{{it}} \right)}{\left(−\mathrm{2}\right)^{\mathrm{2}} −\left({i}\right)^{\mathrm{2}} }+{c} \\ $$$$={e}^{−\mathrm{2}{t}} .\frac{\left(−\mathrm{2}−{i}\right)\left({cost}+{isint}\right)}{\mathrm{4}+\mathrm{1}} \\ $$$$={e}^{−\mathrm{2}{t}} .\frac{\left(−\mathrm{2}{cost}−{i}\mathrm{2}{sint}−{icost}−{i}^{\mathrm{2}} {sint}\right)}{\mathrm{5}} \\ $$$$={e}^{−\mathrm{2}{t}.} \frac{\left(−\mathrm{2}{cost}+{sint}\right)−{i}\left(\mathrm{2}{sint}+{cost}\right)}{\mathrm{5}} \\ $$$${separating}\:{real}\:{and}\:{imaginary}\:{part} \\ $$$$={e}^{−\mathrm{2}{t}} .\frac{\left(−\mathrm{2}{cost}+{sint}\right)}{\mathrm{5}}+{i}\:\frac{{e}^{−\mathrm{2}{t}} \left(−\mathrm{2}{sint}−{cost}\right)}{\mathrm{5}} \\ $$$${so}\:\int{e}^{−\mathrm{2}{t}} {sint}\:{dt}={e}^{−\mathrm{2}{t}} .\frac{\left(−\mathrm{2}{sint}−{cost}\right)}{\mathrm{5}} \\ $$$$={x}^{−\mathrm{2}} .\frac{\left(−\mathrm{2}{sinlnx}−{coslnx}\right)}{\mathrm{5}} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 04/Aug/18
correct answer, I found another way
$$\mathrm{correct}\:\mathrm{answer},\:\mathrm{I}\:\mathrm{found}\:\mathrm{another}\:\mathrm{way} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18
thnk you sir...this platform become combination of thinktank...thank you sir...
$${thnk}\:{you}\:{sir}…{this}\:{platform}\:{become}\:{combination} \\ $$$${of}\:{thinktank}…{thank}\:{you}\:{sir}… \\ $$
Commented by MJS last updated on 04/Aug/18
thank you too
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{too} \\ $$
Answered by MJS last updated on 04/Aug/18
∫((sin ln x)/x^3 )dx= [t=ln x → dx=xdt] =∫e^(−2t) sin t dt=t [((∫f′g=fg−∫fg′)),((f′=e^(−2t) ⇒ f=−(1/2)e^(−2t) )),((g=sin t ⇒ g′=cos t)) ] =−(1/2)e^(−2t) sin t +(1/2)∫e^(−2t) cos t dt= [((∫f′g=fg−∫fg′)),((f′=e^(−2t) ⇒ f=−(1/2)e^(−2t) )),((g=cos t ⇒ g′=−sin t)) ] =−(1/2)e^(−2t) sin t −(1/4)e^(−2t) cos t −(1/4)∫e^(−2t) sin t dt now we have ∫e^(−2t) sin t dt=−(1/2)e^(−2t) sin t −(1/4)e^(−2t) cos t −(1/4)∫e^(−2t) sin t dt (5/4)∫e^(−2t) sin t dt=−(1/2)e^(−2t) sin t −(1/4)e^(−2t) cos t ∫e^(−2t) sin t dt=−(1/5)e^(−2t) (2sin t +cos t) ∫((sin ln x)/x^3 )dx=−(1/(5x^2 ))(2sin ln x +cos ln x)+C
$$\int\frac{\mathrm{sin}\:\mathrm{ln}\:{x}}{{x}^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{ln}\:{x}\:\rightarrow\:{dx}={xdt}\right] \\ $$$$=\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt}=\mathrm{t} \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int{f}'{g}={fg}−\int{fg}'}\\{{f}'=\mathrm{e}^{−\mathrm{2}{t}} \:\Rightarrow\:{f}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} }\\{{g}=\mathrm{sin}\:{t}\:\Rightarrow\:{g}'=\mathrm{cos}\:{t}}\end{bmatrix} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{cos}\:{t}\:{dt}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int{f}'{g}={fg}−\int{fg}'}\\{{f}'=\mathrm{e}^{−\mathrm{2}{t}} \:\Rightarrow\:{f}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} }\\{{g}=\mathrm{cos}\:{t}\:\Rightarrow\:{g}'=−\mathrm{sin}\:{t}}\end{bmatrix} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{cos}\:{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{cos}\:{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt} \\ $$$$\frac{\mathrm{5}}{\mathrm{4}}\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2}{t}} \mathrm{cos}\:{t} \\ $$$$\int\mathrm{e}^{−\mathrm{2}{t}} \mathrm{sin}\:{t}\:{dt}=−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{−\mathrm{2}{t}} \left(\mathrm{2sin}\:{t}\:+\mathrm{cos}\:{t}\right) \\ $$$$\int\frac{\mathrm{sin}\:\mathrm{ln}\:{x}}{{x}^{\mathrm{3}} }{dx}=−\frac{\mathrm{1}}{\mathrm{5}{x}^{\mathrm{2}} }\left(\mathrm{2sin}\:\mathrm{ln}\:{x}\:+\mathrm{cos}\:\mathrm{ln}\:{x}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *