Question Number 41248 by Tawa1 last updated on 04/Aug/18
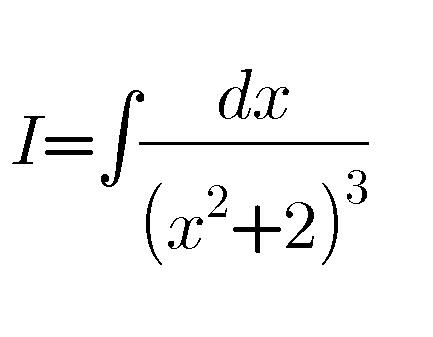
Commented by prof Abdo imad last updated on 04/Aug/18

$${changement}\:{x}=\sqrt{\mathrm{2}}{tant}\:\Rightarrow \\ $$$${I}\:=\:\int\:\:\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}}{\mathrm{8}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\mathrm{3}} }\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\int\:\:\:\frac{{dt}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\int\:{cos}^{\mathrm{4}} {dt}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\int\:\:\:\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)^{\mathrm{2}} {dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:\int\:\:\:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{t}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{sin}\left(\mathrm{2}{t}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:\int\:\frac{\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{t}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{sin}\left(\mathrm{2}{t}\right)\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\:{t}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\:\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{4}{t}\right)\:+{c} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\:{t}\:\:+\:\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:{sin}\left(\mathrm{2}\:{actan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right)\: \\ $$$$+\frac{\sqrt{\mathrm{2}}}{\mathrm{256}}\:{sin}\left(\mathrm{4}\:{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right)\:+{c}\: \\ $$$$\: \\ $$
Commented by prof Abdo imad last updated on 04/Aug/18
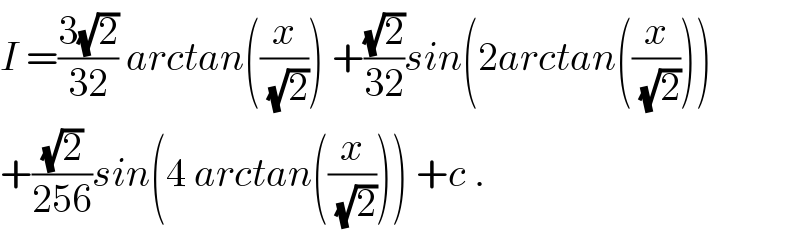
$${I}\:=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\:{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{sin}\left(\mathrm{2}{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right) \\ $$$$+\frac{\sqrt{\mathrm{2}}}{\mathrm{256}}{sin}\left(\mathrm{4}\:{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right)\:+{c}\:. \\ $$
Commented by Tawa1 last updated on 04/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 04/Aug/18

$${thanks}\:{sir} \\ $$
Answered by ajfour last updated on 04/Aug/18
![let x=(√2)tan θ I=∫(((√2)sec^2 θdθ)/(8sec^6 θ)) = ((√2)/8)∫cos^4 θdθ =((√2)/(32))∫(2cos^2 θ)^2 dθ =((√2)/(32))∫(1+cos 2θ)^2 dθ =((√2)/(32))[∫dθ+2∫cos 2θdθ+(1/2)∫(2cos^2 2θ)dθ] = ((√2)/(32))[θ+sin 2θ+(1/2)∫(1+cos 4θ)dθ] =((√2)/(32))[θ+sin 2θ+(θ/2)+((sin 4θ)/8)]+c =((√2)/(32))[(3/2)tan^(−1) (x/( (√2)))+((x(√2))/(1+(x^2 /2)))+((2x(√2)(1−(x^2 /2)))/((1+(x^2 /2))^2 ))]+c .](https://www.tinkutara.com/question/Q41251.png)
$${let}\:\:{x}=\sqrt{\mathrm{2}}\mathrm{tan}\:\theta \\ $$$${I}=\int\frac{\sqrt{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{8sec}\:^{\mathrm{6}} \theta}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\mathrm{cos}\:^{\mathrm{4}} \theta{d}\theta \\ $$$$\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\int\left(\mathrm{2cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{2}} {d}\theta \\ $$$$\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)^{\mathrm{2}} {d}\theta \\ $$$$\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\left[\int{d}\theta+\mathrm{2}\int\mathrm{cos}\:\mathrm{2}\theta{d}\theta+\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}\theta\right){d}\theta\right] \\ $$$$\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\left[\theta+\mathrm{sin}\:\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}\theta\right){d}\theta\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\left[\theta+\mathrm{sin}\:\mathrm{2}\theta+\frac{\theta}{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{8}}\right]+{c} \\ $$$$\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\left[\frac{\mathrm{3}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{2}}}+\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}+\frac{\mathrm{2}{x}\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }\right]+{c}\:. \\ $$
Commented by Tawa1 last updated on 04/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 04/Aug/18
![∫(dx/((x^2 +2)^3 ))= [((reduction formula)),((∫(dx/((ax^2 +b)^n ))=(x/(2b(n−1)(ax^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(dx/((ax^2 +b)^(n−1) )))) ] =(x/(8(x^2 +2)^2 ))+(3/8)∫(dx/((x^2 +2)^2 ))= [same formula again] =(x/(8(x^2 +2)^2 ))+((3x)/(32(x^2 +2)))+(3/(32))∫(dx/(x^2 +2))= [t=((√2)/2)x → dx=dt(√2)] =((x(3x^2 +10))/(32(x^2 +2)^2 ))+((3(√2))/(64))∫(dt/(t^2 +1))= =((x(3x^2 +10))/(32(x^2 +2)^2 ))+((3(√2))/(64))arctan t = =((x(3x^2 +10))/(32(x^2 +2)^2 ))+((3(√2))/(64))arctan ((x(√2))/2) +C](https://www.tinkutara.com/question/Q41282.png)
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\mathrm{reduction}\:\mathrm{formula}}\\{\int\frac{{dx}}{\left({ax}^{\mathrm{2}} +{b}\right)^{{n}} }=\frac{{x}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }+\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)}\int\frac{{dx}}{\left({ax}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }}\end{bmatrix} \\ $$$$=\frac{{x}}{\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{8}}\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{same}\:\mathrm{formula}\:\mathrm{again}\right] \\ $$$$=\frac{{x}}{\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}{x}}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)}+\frac{\mathrm{3}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{x}\:\rightarrow\:{dx}={dt}\sqrt{\mathrm{2}}\right] \\ $$$$=\frac{{x}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{10}\right)}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{{x}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{10}\right)}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{arctan}\:{t}\:= \\ $$$$=\frac{{x}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{10}\right)}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{arctan}\:\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\:+{C} \\ $$
Commented by Tawa1 last updated on 05/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
