Question Number 41252 by ajfour last updated on 04/Aug/18
Commented by ajfour last updated on 04/Aug/18
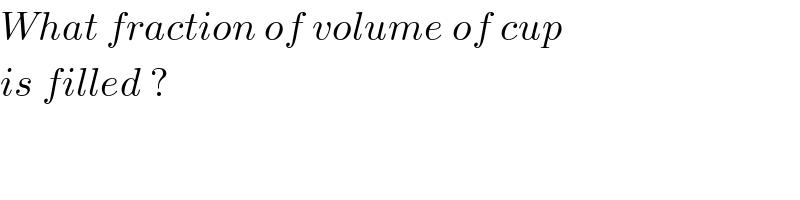
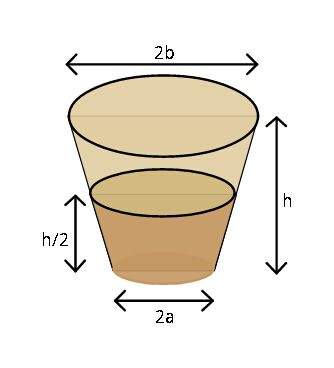
$${What}\:{fraction}\:{of}\:{volume}\:{of}\:{cup} \\ $$$${is}\:{filled}\:? \\ $$
Answered by MrW3 last updated on 05/Aug/18
![volume of cup: V_c =((πh)/3)(a^2 +b^2 +ab) volume of water: V_w =((πh)/6)[a^2 +(((a+b)/2))^2 +a(((a+b)/2))]=((πh)/(24))(7a^2 +b^2 +4ab) ⇒η=(V_w /V_c )=((7a^2 +b^2 +4ab)/(8(a^2 +b^2 +ab)))](https://www.tinkutara.com/question/Q41256.png)
$${volume}\:{of}\:{cup}: \\ $$$${V}_{{c}} =\frac{\pi{h}}{\mathrm{3}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right) \\ $$$${volume}\:{of}\:{water}: \\ $$$${V}_{{w}} =\frac{\pi{h}}{\mathrm{6}}\left[{a}^{\mathrm{2}} +\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +{a}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\right]=\frac{\pi{h}}{\mathrm{24}}\left(\mathrm{7}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{4}{ab}\right) \\ $$$$\Rightarrow\eta=\frac{{V}_{{w}} }{{V}_{{c}} }=\frac{\mathrm{7}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{4}{ab}}{\mathrm{8}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)} \\ $$
Commented by ajfour last updated on 04/Aug/18
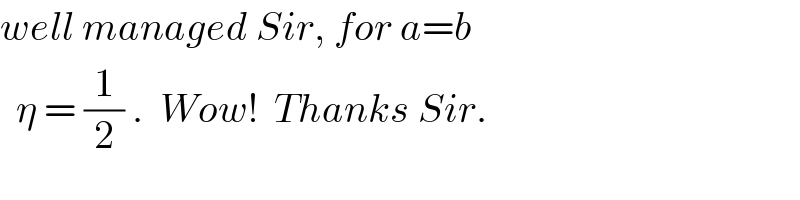
$${well}\:{managed}\:{Sir},\:{for}\:{a}={b}\: \\ $$$$\:\:\eta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:.\:\:{Wow}!\:\:{Thanks}\:{Sir}. \\ $$
