Question-41255

Question Number 41255 by ajfour last updated on 04/Aug/18

Commented by ajfour last updated on 04/Aug/18

The natural length of spring is l and if realeased as shown, find speed of ring as it reaches the ground. μ is the friction coefficient between vertical rod and the ring.

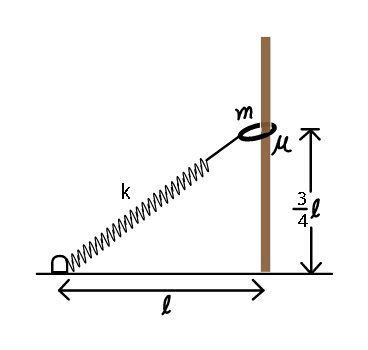
$${The}\:{natural}\:{length}\:{of}\:{spring}\:{is} \\ $$$${l}\:{and}\:{if}\:{realeased}\:{as}\:{shown},\:{find} \\ $$$${speed}\:{of}\:{ring}\:{as}\:{it}\:{reaches}\:{the} \\ $$$${ground}.\:\mu\:{is}\:{the}\:{friction}\:{coefficient} \\ $$$${between}\:{vertical}\:{rod}\:{and}\:{the}\:{ring}. \\ $$

Answered by ajfour last updated on 05/Aug/18

At an intermediate position, let the angle of spring line with horizontal be θ. Normal reaction on ring N=kxcos θ x=l(sec θ−1) friction f = μkl(1−cos θ) height of ring is y=ltan θ dy = lsec^2 θdθ W_f =∫_α ^( 0) μkl^2 (1−cos θ)sec^2 θdθ where α = tan^(−1) ((3/4)) ⇒ W_f =−μkl^2 ∫_0 ^( α) (sec^2 θ−sec θ)dθ =−μkl^2 [tan α−ln (sec α+tan α)] =−μkl^2 [(3/4)−ln ((5/4)+(3/4))] =−μkl^2 ((3/4)−ln 2) (1/2)mv^2 = mg(((3l)/4))+(1/2)k[lsec α−l]^2 −μkl^2 ((3/4)−ln 2) v^2 = ((3gl)/2)+((kl^2 )/(16m))−((μkl^2 )/m)((3/2)−2ln 2) v =(√(((3gl)/2)+((kl^2 )/(16m))−((μkl^2 )/m)((3/2)−2ln 2))) .

$${At}\:{an}\:{intermediate}\:{position},\:{let} \\ $$$${the}\:{angle}\:{of}\:{spring}\:{line}\:{with} \\ $$$${horizontal}\:{be}\:\theta. \\ $$$${Normal}\:{reaction}\:{on}\:{ring} \\ $$$$\:\:\:\:\:\:{N}={kx}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:{x}={l}\left(\mathrm{sec}\:\theta−\mathrm{1}\right) \\ $$$${friction}\:\boldsymbol{{f}}\:=\:\mu{kl}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${height}\:{of}\:{ring}\:{is}\:\:\boldsymbol{{y}}={l}\mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:{dy}\:=\:{l}\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:{W}_{{f}} \:=\int_{\alpha} ^{\:\:\mathrm{0}} \mu{kl}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:\:{where}\:\:\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\:\:{W}_{{f}} \:=−\mu{kl}^{\mathrm{2}} \int_{\mathrm{0}} ^{\:\:\alpha} \left(\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{sec}\:\theta\right){d}\theta \\ $$$$\:\:\:\:\:\:\:=−\mu{kl}^{\mathrm{2}} \left[\mathrm{tan}\:\alpha−\mathrm{ln}\:\left(\mathrm{sec}\:\alpha+\mathrm{tan}\:\alpha\right)\right] \\ $$$$=−\mu{kl}^{\mathrm{2}} \left[\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{ln}\:\left(\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}\right)\right] \\ $$$$\:\:=−\mu{kl}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{ln}\:\mathrm{2}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} =\:{mg}\left(\frac{\mathrm{3}{l}}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{k}\left[{l}\mathrm{sec}\:\alpha−{l}\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mu{kl}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{ln}\:\mathrm{2}\right) \\ $$$${v}^{\mathrm{2}} =\:\frac{\mathrm{3}{gl}}{\mathrm{2}}+\frac{{kl}^{\mathrm{2}} }{\mathrm{16}{m}}−\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2ln}\:\mathrm{2}\right) \\ $$$$\boldsymbol{{v}}\:=\sqrt{\frac{\mathrm{3}{gl}}{\mathrm{2}}+\frac{{kl}^{\mathrm{2}} }{\mathrm{16}{m}}−\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2ln}\:\mathrm{2}\right)}\:. \\ $$

Commented by MrW3 last updated on 05/Aug/18

$${great}\:{job}! \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18

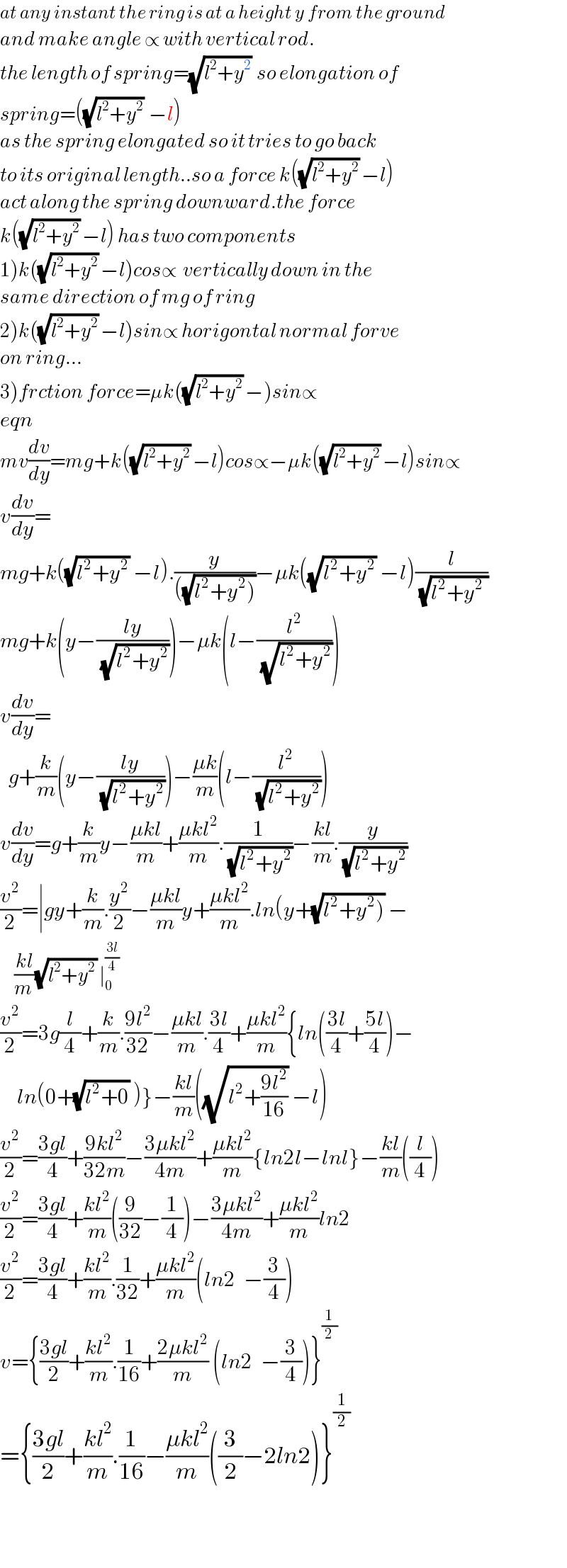
at any instant the ring is at a height y from the ground and make angle ∝ with vertical rod. the length of spring=(√(l^2 +y_ ^2 )) so elongation of spring=((√(l^2 +y^2 )) −l) as the spring elongated so it tries to go back to its original length..so a force k((√(l^2 +y^2 )) −l) act along the spring downward.the force k((√(l^2 +y^2 )) −l) has two components 1)k((√(l^2 +y^2 )) −l)cos∝ vertically down in the same direction of mg of ring 2)k((√(l^2 +y^2 )) −l)sin∝ horigontal normal forve on ring... 3)frction force=μk((√(l^2 +y^2 )) −)sin∝ eqn mv(dv/dy)=mg+k((√(l^2 +y^2 )) −l)cos∝−μk((√(l^2 +y^2 )) −l)sin∝ v(dv/dy)= mg+k((√(l^2 +y^2 )) −l).(y/(((√(l^2 +y^2 )))))−μk((√(l^2 +y_ ^2 )) −l)(l/( (√(l^2 +y^2 )))) mg+k(y−((ly)/( (√(l_ ^2 +y^2 )))))−μk(l−(l^2 /( (√(l^2 +y^2 _ ))))) v(dv/dy)= g+(k/m)(y−((ly)/( (√(l^2 +y^2 )))))−((μk)/m)(l−(l^2 /( (√(l^2 +y^2 ))))) v(dv/dy)=g+(k/m)y−((μkl)/m)+((μkl^2 )/m).(1/( (√(l^2 +y^2 ))))−((kl)/m).(y/( (√(l^2 +y^2 )))) (v^2 /2)=∣gy+(k/m).(y^2 /2)−((μkl)/m)y+((μkl^2 )/m).ln(y+(√(l^2 +y^2 ))) − ((kl)/(m ))(√(l^2 +y^(2 ) )) ∣_0 ^((3l)/4) (v^2 /2)=3g(l/4)+(k/m).((9l^2 )/(32))−((μkl)/m).((3l)/4)+((μkl^2 )/m){ln(((3l)/4)+((5l)/4))− ln(0+(√(l^2 +0)) )}−((kl)/m)((√(l^2 +((9l^2 )/(16)))) −l) (v^2 /2)=((3gl)/4)+((9kl^2 )/(32m))−((3μkl^2 )/(4m))+((μkl^2 )/m){ln2l−lnl}−((kl)/m)((l/4)) (v^2 /2)=((3gl)/4)+((kl^2 )/m)((9/(32))−(1/4))−((3μkl^2 )/(4m))+((μkl^2 )/m)ln2 (v^2 /2)=((3gl)/4)+((kl^2 )/m).(1/(32))+((μkl^2 )/m)(ln2 −(3/4)) v={((3gl)/2)+((kl^2 )/m).(1/(16))+((2μkl^2 )/m) (ln2 −(3/4))}^(1/2) ={((3gl)/2)+((kl^2 )/m).(1/(16))−((μkl^2 )/m)((3/2)−2ln2)}^(1/2)

$${at}\:{any}\:{instant}\:{the}\:{ring}\:{is}\:{at}\:{a}\:{height}\:{y}\:{from}\:{the}\:{ground} \\ $$$${and}\:{make}\:{angle}\:\propto\:{with}\:{vertical}\:{rod}. \\ $$$${the}\:{length}\:{of}\:{spring}=\sqrt{{l}^{\mathrm{2}} +{y}_{\:} ^{\mathrm{2}} }\:\:{so}\:{elongation}\:{of} \\ $$$${spring}=\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:−{l}\right) \\ $$$${as}\:{the}\:{spring}\:{elongated}\:{so}\:{it}\:{tries}\:{to}\:{go}\:{back} \\ $$$${to}\:{its}\:{original}\:{length}..{so}\:{a}\:{force}\:{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right) \\ $$$${act}\:{along}\:{the}\:{spring}\:{downward}.{the}\:{force} \\ $$$${k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right)\:{has}\:{two}\:{components} \\ $$$$\left.\mathrm{1}\right){k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right){cos}\propto\:\:{vertically}\:{down}\:{in}\:{the} \\ $$$${same}\:{direction}\:{of}\:{mg}\:{of}\:{ring} \\ $$$$\left.\mathrm{2}\right){k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right){sin}\propto\:{horigontal}\:{normal}\:{forve} \\ $$$${on}\:{ring}… \\ $$$$\left.\mathrm{3}\right){frction}\:{force}=\mu{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−\right){sin}\propto \\ $$$${eqn} \\ $$$${mv}\frac{{dv}}{{dy}}={mg}+{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right){cos}\propto−\mu{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right){sin}\propto \\ $$$${v}\frac{{dv}}{{dy}}= \\ $$$${mg}+{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:−{l}\right).\frac{{y}}{\left(\sqrt{\left.{l}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}\right.}−\mu{k}\left(\sqrt{{l}^{\mathrm{2}} +{y}_{} ^{\mathrm{2}} }\:−{l}\right)\frac{{l}}{\:\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} \:}} \\ $$$${mg}+{k}\left({y}−\frac{{ly}}{\:\sqrt{{l}_{} ^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right)−\mu{k}\left({l}−\frac{{l}^{\mathrm{2}} }{\:\sqrt{{l}^{\mathrm{2}} +\underset{} {{y}}^{\mathrm{2}} }}\right) \\ $$$${v}\frac{{dv}}{{dy}}= \\ $$$$\:\:{g}+\frac{{k}}{{m}}\left({y}−\frac{{ly}}{\:\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right)−\frac{\mu{k}}{{m}}\left({l}−\frac{{l}^{\mathrm{2}} }{\:\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\right) \\ $$$${v}\frac{{dv}}{{dy}}={g}+\frac{{k}}{{m}}{y}−\frac{\mu{kl}}{{m}}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}.\frac{\mathrm{1}}{\:\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }}−\frac{{kl}}{{m}}.\frac{{y}}{\:\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\mid{gy}+\frac{{k}}{{m}}.\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mu{kl}}{{m}}{y}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}.{ln}\left({y}+\sqrt{\left.{l}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}\:−\right. \\ $$$$\:\:\:\:\:\frac{{kl}}{{m}\:}\sqrt{{l}^{\mathrm{2}} +{y}^{\mathrm{2}\:} }\:\mid_{\mathrm{0}} ^{\frac{\mathrm{3}{l}}{\mathrm{4}}} \: \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{3}{g}\frac{{l}}{\mathrm{4}}+\frac{{k}}{{m}}.\frac{\mathrm{9}{l}^{\mathrm{2}} }{\mathrm{32}}−\frac{\mu{kl}}{{m}}.\frac{\mathrm{3}{l}}{\mathrm{4}}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left\{{ln}\left(\frac{\mathrm{3}{l}}{\mathrm{4}}+\frac{\mathrm{5}{l}}{\mathrm{4}}\right)−\right. \\ $$$$\left.\:\:\:\:{ln}\left(\mathrm{0}+\sqrt{{l}^{\mathrm{2}} +\mathrm{0}}\:\right)\right\}−\frac{{kl}}{{m}}\left(\sqrt{{l}^{\mathrm{2}} +\frac{\mathrm{9}{l}^{\mathrm{2}} }{\mathrm{16}}}\:−{l}\right) \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}{gl}}{\mathrm{4}}+\frac{\mathrm{9}{kl}^{\mathrm{2}} }{\mathrm{32}{m}}−\frac{\mathrm{3}\mu{kl}^{\mathrm{2}} }{\mathrm{4}{m}}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left\{{ln}\mathrm{2}{l}−{lnl}\right\}−\frac{{kl}}{{m}}\left(\frac{{l}}{\mathrm{4}}\right) \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}{gl}}{\mathrm{4}}+\frac{{kl}^{\mathrm{2}} }{{m}}\left(\frac{\mathrm{9}}{\mathrm{32}}−\frac{\mathrm{1}}{\mathrm{4}}\right)−\frac{\mathrm{3}\mu{kl}^{\mathrm{2}} }{\mathrm{4}{m}}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}{ln}\mathrm{2} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}{gl}}{\mathrm{4}}+\frac{{kl}^{\mathrm{2}} }{{m}}.\frac{\mathrm{1}}{\mathrm{32}}+\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left({ln}\mathrm{2}\:\:−\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${v}=\left\{\frac{\mathrm{3}{gl}}{\mathrm{2}}+\frac{{kl}^{\mathrm{2}} }{{m}}.\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{2}\mu{kl}^{\mathrm{2}} }{{m}}\:\left({ln}\mathrm{2}\:\:−\frac{\mathrm{3}}{\mathrm{4}}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left\{\frac{\mathrm{3}{gl}}{\mathrm{2}}+\frac{{kl}^{\mathrm{2}} }{{m}}.\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mu{kl}^{\mathrm{2}} }{{m}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2}{ln}\mathrm{2}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$

Commented by MrW3 last updated on 04/Aug/18

$${very}\:{nice}! \\ $$

Commented by MrW3 last updated on 05/Aug/18

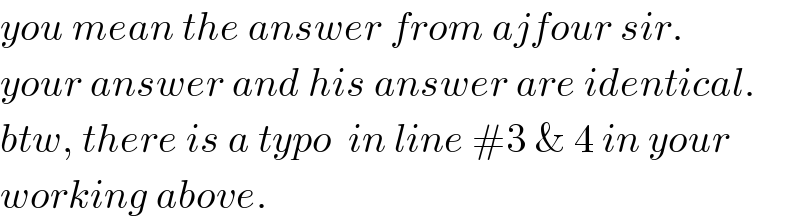
you mean the answer from ajfour sir. your answer and his answer are identical. btw, there is a typo in line #3 & 4 in your working above.

$${you}\:{mean}\:{the}\:{answer}\:{from}\:{ajfour}\:{sir}. \\ $$$${your}\:{answer}\:{and}\:{his}\:{answer}\:{are}\:{identical}. \\ $$$${btw},\:{there}\:{is}\:{a}\:{typo}\:\:{in}\:{line}\:#\mathrm{3}\:\&\:\mathrm{4}\:{in}\:{your} \\ $$$${working}\:{above}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 04/Aug/18

$${yes}\:{sir}\:{i}\:{have}\:{rectified}\:{it}…{yours}\:{amd}\:{myself} \\ $$$${answer}\:{become}\:{identical}…{thank}\:{you}\:..{you}\:{hahe} \\ $$$${given}\:{your}\:{time}\:{to}\:{go}\:{throuvh}\:{my}\:{post}… \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Aug/18