Menu Close

Question-41324

Tinku Tara 0 Comments
Pin




Question Number 41324 by ajfour last updated on 05/Aug/18
Commented by ajfour last updated on 05/Aug/18
How to construct the dotted blue circle passing through A and tangent to the shown line such that the red line is horizontal. (construction methods only please).
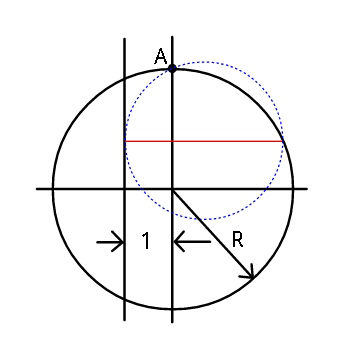
$${How}\:{to}\:{construct}\:{the}\:{dotted}\:{blue} \\ $$$${circle}\:\:{passing}\:{through}\:{A}\:{and} \\ $$$${tangent}\:{to}\:{the}\:{shown}\:{line}\:{such} \\ $$$${that}\:{the}\:{red}\:{line}\:{is}\:{horizontal}. \\ $$$$\left({construction}\:{methods}\:{only}\:{please}\right). \\ $$
Commented by MJS last updated on 06/Aug/18
A= ((0),(R) ) M= (((r−1)),(y) ) B= (((2r−1)),(y) ) ∣OB∣^2 −R^2 =0 ∣MA∣^2 −r^2 =0 (2r−1)^2 +y^2 −R^2 =0 ⇒ y^2 =−4r^2 +4r+R^2 −1 (r−1)^2 +(y−R)^2 −r^2 =0 ⇒ y^2 =2r+2Ry−R^2 −1 −4r^2 +4r+R^2 −1=2r+2Ry−R^2 −1 y=((−2r^2 +r+R^2 )/R) (((−2r^2 +r+R^2 )/R))^2 =−4r^2 +4r+R^2 −1 r^4 −r^3 +(1/4)r^2 −(R^2 /2)r+(R^2 /4)=0 (r−(1/2))(r^3 −(1/2)r^2 −(R^2 /2))=0 (r=(1/2) ⇒ y=R; M= (((−(1/2))),(R) ) B=A) r^3 −(1/2)r^2 −(R^2 /2)=0 r=z+(1/6) z^3 −(1/(12))z−((R^2 /2)+(1/(108)))=0 z=(1/6)(((54R^2 +1+(√(81R^2 +3))))^(1/3) +((54R^2 +1−(√(81R^2 +3))))^(1/3) ) r=(1/6)(1+((54R^2 +1+(√(81R^2 +3))))^(1/3) +((54R^2 +1−(√(81R^2 +3))))^(1/3) ) I don′t think we can construct this... interestingly r∈Q for some values of R∈Q found it by trying R∈N (R/r)= ={(0/(1/2)), (1/(1/1)), (5/(5/2)), (15/((15)/3)), (34/((34)/4)), (65/((65)/5)), ...} this leads to R=(1/2)n^3 −(3/2)n^2 +2n−1 r=(1/2)n^2 −n+1 y=(1/2)n^3 −(3/2)n+n ⇒ n∈Q ⇒ R, r, y ∈Q
$${A}=\begin{pmatrix}{\mathrm{0}}\\{{R}}\end{pmatrix}\:\:{M}=\begin{pmatrix}{{r}−\mathrm{1}}\\{{y}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{2}{r}−\mathrm{1}}\\{{y}}\end{pmatrix} \\ $$$$\mid{OB}\mid^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mid{MA}\mid^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{y}^{\mathrm{2}} =−\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+{R}^{\mathrm{2}} −\mathrm{1} \\ $$$$\left({r}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{y}^{\mathrm{2}} =\mathrm{2}{r}+\mathrm{2}{Ry}−{R}^{\mathrm{2}} −\mathrm{1} \\ $$$$−\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+{R}^{\mathrm{2}} −\mathrm{1}=\mathrm{2}{r}+\mathrm{2}{Ry}−{R}^{\mathrm{2}} −\mathrm{1} \\ $$$${y}=\frac{−\mathrm{2}{r}^{\mathrm{2}} +{r}+{R}^{\mathrm{2}} }{{R}} \\ $$$$\left(\frac{−\mathrm{2}{r}^{\mathrm{2}} +{r}+{R}^{\mathrm{2}} }{{R}}\right)^{\mathrm{2}} =−\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+{R}^{\mathrm{2}} −\mathrm{1} \\ $$$${r}^{\mathrm{4}} −{r}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{4}}{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{2}}{r}+\frac{{R}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\left({r}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({r}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\left({r}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{y}={R};\:{M}=\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}}\\{{R}}\end{pmatrix}\:\:{B}={A}\right) \\ $$$${r}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} −\frac{{R}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$${r}={z}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{12}}{z}−\left(\frac{{R}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{108}}\right)=\mathrm{0} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{6}}\left(\sqrt[{\mathrm{3}}]{\mathrm{54}{R}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{81}{R}^{\mathrm{2}} +\mathrm{3}}}+\sqrt[{\mathrm{3}}]{\mathrm{54}{R}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{81}{R}^{\mathrm{2}} +\mathrm{3}}}\right) \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\mathrm{54}{R}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{81}{R}^{\mathrm{2}} +\mathrm{3}}}+\sqrt[{\mathrm{3}}]{\mathrm{54}{R}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{81}{R}^{\mathrm{2}} +\mathrm{3}}}\right) \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{construct}\:\mathrm{this}… \\ $$$$\mathrm{interestingly}\:{r}\in\mathbb{Q}\:\mathrm{for}\:\mathrm{some}\:\mathrm{values}\:\mathrm{of}\:{R}\in\mathbb{Q} \\ $$$$\mathrm{found}\:\mathrm{it}\:\mathrm{by}\:\mathrm{trying}\:{R}\in\mathbb{N} \\ $$$$\left({R}/{r}\right)= \\ $$$$=\left\{\left(\mathrm{0}/\frac{\mathrm{1}}{\mathrm{2}}\right),\:\left(\mathrm{1}/\frac{\mathrm{1}}{\mathrm{1}}\right),\:\left(\mathrm{5}/\frac{\mathrm{5}}{\mathrm{2}}\right),\:\left(\mathrm{15}/\frac{\mathrm{15}}{\mathrm{3}}\right),\:\left(\mathrm{34}/\frac{\mathrm{34}}{\mathrm{4}}\right),\:\left(\mathrm{65}/\frac{\mathrm{65}}{\mathrm{5}}\right),\:…\right\} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{1} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} −{n}+\mathrm{1} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}{n}+{n} \\ $$$$\Rightarrow\:{n}\in\mathbb{Q}\:\Rightarrow\:{R},\:{r},\:{y}\:\in\mathbb{Q} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Aug/18
1)first draw big circle centre(0,0) and radius R assuming R=any value 2)draw line x+1=0 let red line (y=d)cut x+1=0 at point B(−1,d) 3)pointA(0,R) 4)now let red line is y=d let red line cut yaxis at point C(0,d) let small circle cut big circle at points A and D A(0,R)and C(0,d) solve y=d and x^2 +y^2 =R^2 x=(√(R^2 −d^2 )) so point D((√(R^2 −d^(2 ) )) ,d) now we have to find value of d let the length of red line is =1+(√(R^2 −d^2 )) CD^2 =AC.CA_1 point A_1 diametrically opposite of A so CD^2 =(R−d)(R+d) AB^2 +AD^2 =BD^2 A(0,R) B(−1,d) and D((√(R^2 −d^2 )) ,d) 1^2 +(R−d)^2 +R^2 −d^2 +(R−d)^2 ={1+(√(R^2 −d^2 ))}^2 1+2(R−d)^2 +R^2 −d^2 =1+2(√(R^2 −d^2 )) +R^2 −d^2 (R−d)^2 =(√(R^2 −d^2 )) from this eqn we get value of d in in terms of R then draw red line y=d that is diameter of smallcircle then we draw small circle ...pls check...
$$\left.\mathrm{1}\right){first}\:{draw}\:{big}\:{circle}\:{centre}\left(\mathrm{0},\mathrm{0}\right)\:{and}\:{radius}\:{R} \\ $$$$\:{assuming}\:{R}={any}\:{value} \\ $$$$\left.\mathrm{2}\right){draw}\:{line}\:{x}+\mathrm{1}=\mathrm{0} \\ $$$${let}\:{red}\:{line}\:\left({y}={d}\right){cut}\:{x}+\mathrm{1}=\mathrm{0}\:{at}\:{point}\:{B}\left(−\mathrm{1},{d}\right) \\ $$$$\left.\mathrm{3}\right){pointA}\left(\mathrm{0},{R}\right) \\ $$$$\left.\mathrm{4}\right){now}\:{let}\:{red}\:{line}\:{is}\:{y}={d} \\ $$$${let}\:{red}\:{line}\:{cut}\:{yaxis}\:{at}\:{point}\:{C}\left(\mathrm{0},{d}\right) \\ $$$${let}\:{small}\:{circle}\:{cut}\:{big}\:{circle}\:{at}\:{points}\:{A}\:{and}\:{D} \\ $$$${A}\left(\mathrm{0},{R}\right){and}\:{C}\left(\mathrm{0},{d}\right) \\ $$$${solve}\:{y}={d}\:{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${x}=\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\:\:{so}\:{point}\:{D}\left(\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}\:} }\:\:,{d}\right) \\ $$$${now}\:{we}\:{have}\:{to}\:{find}\:{value}\:{of}\:{d} \\ $$$${let}\:{the}\:{length}\:{of}\:{red}\:{line}\:{is}\:=\mathrm{1}+\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\:\: \\ $$$${CD}^{\mathrm{2}} ={AC}.{CA}_{\mathrm{1}} \:\:{point}\:{A}_{\mathrm{1}} {diametrically}\:{opposite}\:{of}\:{A} \\ $$$$\:\:{so}\:\:{CD}^{\mathrm{2}} =\left({R}−{d}\right)\left({R}+{d}\right) \\ $$$$ \\ $$$${AB}^{\mathrm{2}} +{AD}^{\mathrm{2}} ={BD}^{\mathrm{2}} \\ $$$${A}\left(\mathrm{0},{R}\right)\:\:{B}\left(−\mathrm{1},{d}\right)\:{and}\:{D}\left(\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\:\:,{d}\right) \\ $$$$\mathrm{1}^{\mathrm{2}} +\left({R}−{d}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −{d}^{\mathrm{2}} +\left({R}−{d}\right)^{\mathrm{2}} =\left\{\mathrm{1}+\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\right\}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{2}\left({R}−{d}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −{d}^{\mathrm{2}} \:=\mathrm{1}+\mathrm{2}\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\:\:\:+{R}^{\mathrm{2}} −{d}^{\mathrm{2}} \\ $$$$\left({R}−{d}\right)^{\mathrm{2}} =\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }\:\:\:{from}\:{this}\:{eqn}\:{we}\:{get}\:{value} \\ $$$${of}\:{d}\:{in}\:{in}\:{terms}\:{of}\:{R} \\ $$$${then}\:{draw}\:{red}\:{line}\:{y}={d}\:\:{that}\:{is}\:{diameter}\:{of} \\ $$$${smallcircle}\: \\ $$$${then}\:{we}\:{draw}\:{small}\:{circle} \\ $$$$…\boldsymbol{{pls}}\:\boldsymbol{{check}}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 06/Aug/18
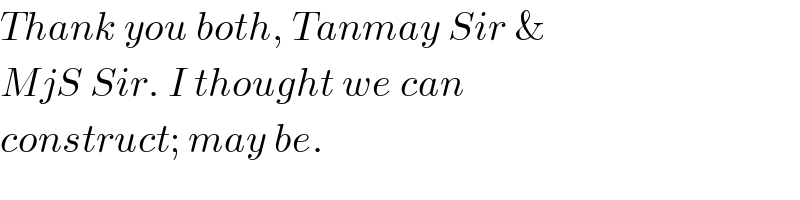
Thank you both, Tanmay Sir & MjS Sir. I thought we can construct; may be.
$${Thank}\:{you}\:{both},\:{Tanmay}\:{Sir}\:\& \\ $$$${MjS}\:{Sir}.\:{I}\:{thought}\:{we}\:{can} \\ $$$${construct};\:{may}\:{be}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *