Question-41347

Question Number 41347 by behi83417@gmail.com last updated on 06/Aug/18

Answered by MJS last updated on 06/Aug/18

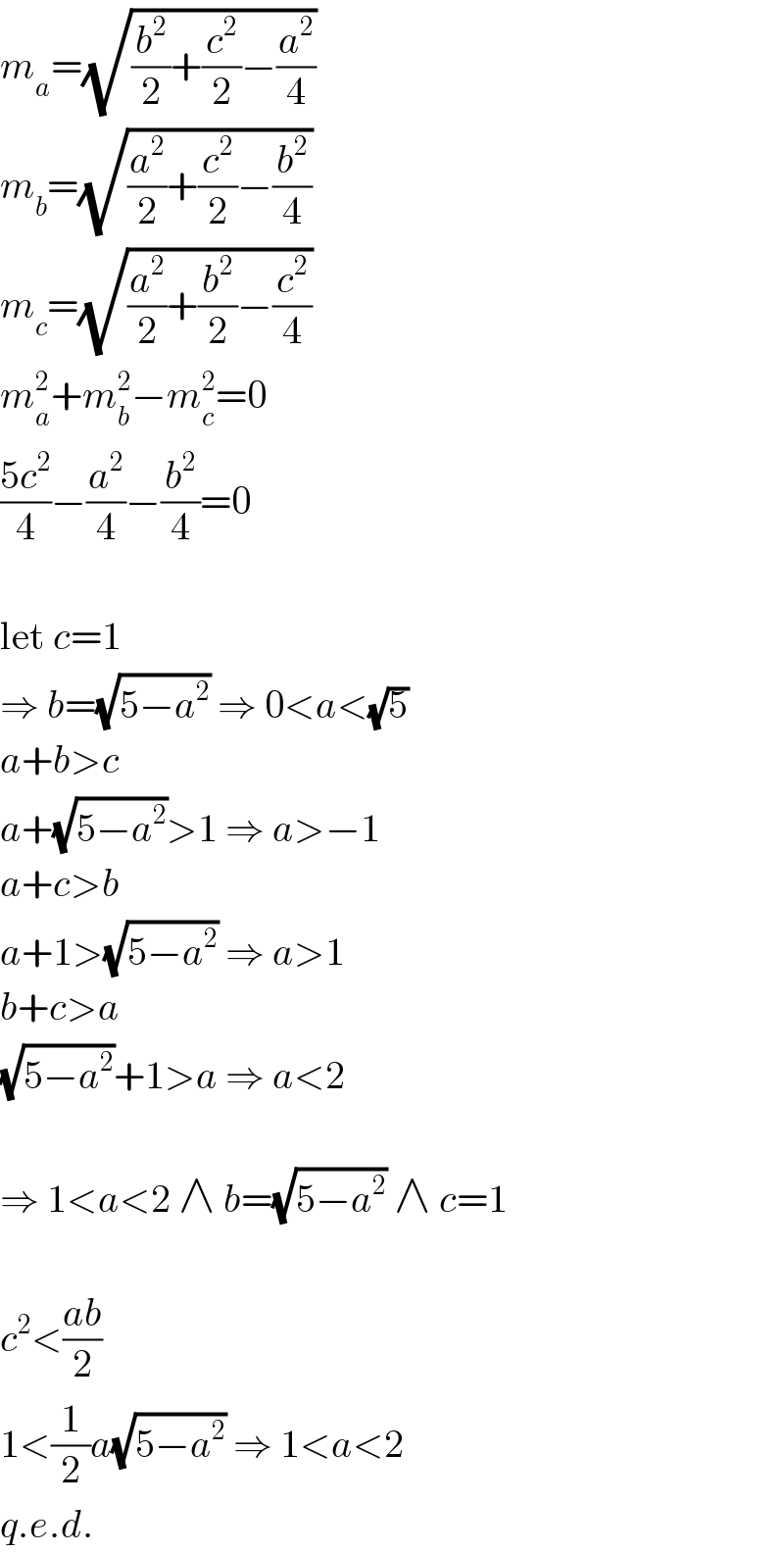
m_a =(√((b^2 /2)+(c^2 /2)−(a^2 /4))) m_b =(√((a^2 /2)+(c^2 /2)−(b^2 /4))) m_c =(√((a^2 /2)+(b^2 /2)−(c^2 /4))) m_a ^2 +m_b ^2 −m_c ^2 =0 ((5c^2 )/4)−(a^2 /4)−(b^2 /4)=0 let c=1 ⇒ b=(√(5−a^2 )) ⇒ 0<a<(√5) a+b>c a+(√(5−a^2 ))>1 ⇒ a>−1 a+c>b a+1>(√(5−a^2 )) ⇒ a>1 b+c>a (√(5−a^2 ))+1>a ⇒ a<2 ⇒ 1<a<2 ∧ b=(√(5−a^2 )) ∧ c=1 c^2 <((ab)/2) 1<(1/2)a(√(5−a^2 )) ⇒ 1<a<2 q.e.d.

$${m}_{{a}} =\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{2}}+\frac{{c}^{\mathrm{2}} }{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${m}_{{b}} =\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{{c}^{\mathrm{2}} }{\mathrm{2}}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${m}_{{c}} =\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{{b}^{\mathrm{2}} }{\mathrm{2}}−\frac{{c}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$${m}_{{a}} ^{\mathrm{2}} +{m}_{{b}} ^{\mathrm{2}} −{m}_{{c}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{5}{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{let}\:{c}=\mathrm{1} \\ $$$$\Rightarrow\:{b}=\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{0}<{a}<\sqrt{\mathrm{5}} \\ $$$${a}+{b}>{c} \\ $$$${a}+\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }>\mathrm{1}\:\Rightarrow\:{a}>−\mathrm{1} \\ $$$${a}+{c}>{b} \\ $$$${a}+\mathrm{1}>\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }\:\Rightarrow\:{a}>\mathrm{1} \\ $$$${b}+{c}>{a} \\ $$$$\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }+\mathrm{1}>{a}\:\Rightarrow\:{a}<\mathrm{2} \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{1}<{a}<\mathrm{2}\:\wedge\:{b}=\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }\:\wedge\:{c}=\mathrm{1} \\ $$$$ \\ $$$${c}^{\mathrm{2}} <\frac{{ab}}{\mathrm{2}} \\ $$$$\mathrm{1}<\frac{\mathrm{1}}{\mathrm{2}}{a}\sqrt{\mathrm{5}−{a}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{1}<{a}<\mathrm{2} \\ $$$${q}.{e}.{d}. \\ $$

Commented by behi83417@gmail.com last updated on 06/Aug/18

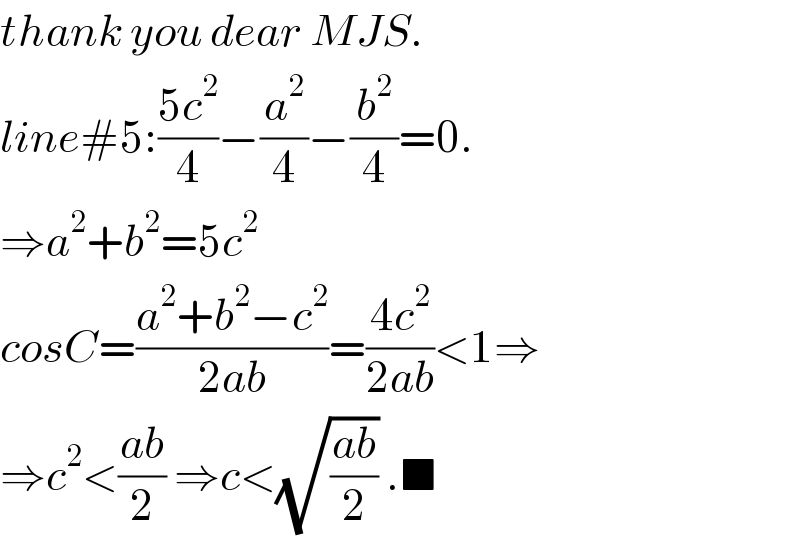
thank you dear MJS. line#5:((5c^2 )/4)−(a^2 /4)−(b^2 /4)=0. ⇒a^2 +b^2 =5c^2 cosC=((a^2 +b^2 −c^2 )/(2ab))=((4c^2 )/(2ab))<1⇒ ⇒c^2 <((ab)/2) ⇒c<(√((ab)/2)) .■

$${thank}\:{you}\:{dear}\:{MJS}. \\ $$$${line}#\mathrm{5}:\frac{\mathrm{5}{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0}. \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5}{c}^{\mathrm{2}} \\ $$$${cosC}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}=\frac{\mathrm{4}{c}^{\mathrm{2}} }{\mathrm{2}{ab}}<\mathrm{1}\Rightarrow \\ $$$$\Rightarrow{c}^{\mathrm{2}} <\frac{{ab}}{\mathrm{2}}\:\Rightarrow{c}<\sqrt{\frac{{ab}}{\mathrm{2}}}\:.\blacksquare \\ $$

Commented by MJS last updated on 06/Aug/18

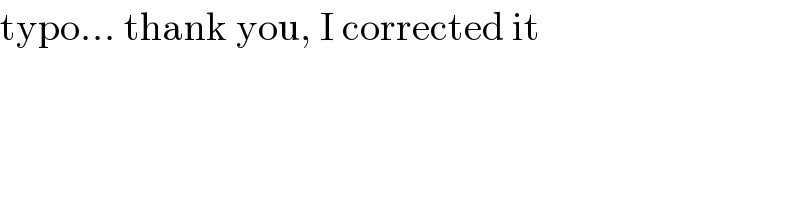
$$\mathrm{typo}…\:\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply