Question-41431

Question Number 41431 by Tawa1 last updated on 07/Aug/18

Commented by tanmay.chaudhury50@gmail.com last updated on 08/Aug/18

f(x)=((x^2 +4lnx+ln3)/(x^2 −5x+3)) 1)D(x)=x^2 −5x+3 finding zeroes for x^2 −5x+3 x^2 −5x+3=0 x=((5±(√(25−12)))/2)=((5±(√(13)))/2) D(x) is defined for all values of x except ((5±(√(13)))/2) 2)given 8 ≥x≥0 but at x=0 ,lnx is undefined so f(x) is defined at values of x except x=0 and x =((5±(√(13)))/2) contd

$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} +\mathrm{4}{lnx}+{ln}\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}} \\ $$$$\left.\mathrm{1}\right){D}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3} \\ $$$${finding}\:{zeroes}\:{for}\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{12}}}{\mathrm{2}}=\frac{\mathrm{5}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$${D}\left({x}\right)\:{is}\:{defined}\:{for}\:{all}\:{values}\:{of}\:{x}\:{except}\: \\ $$$$\frac{\mathrm{5}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){given}\:\:\mathrm{8}\:\geqslant{x}\geqslant\mathrm{0}\:\:{but}\:{at}\:{x}=\mathrm{0}\:,{lnx}\:{is}\:{undefined} \\ $$$${so}\:{f}\left({x}\right)\:{is}\:{defined}\:{at}\:{values}\:{of}\:{x}\:\boldsymbol{{except}}\:\boldsymbol{{x}}=\mathrm{0} \\ $$$$\:\:{and}\:\boldsymbol{{x}}\:=\frac{\mathrm{5}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$${contd} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 08/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 08/Aug/18

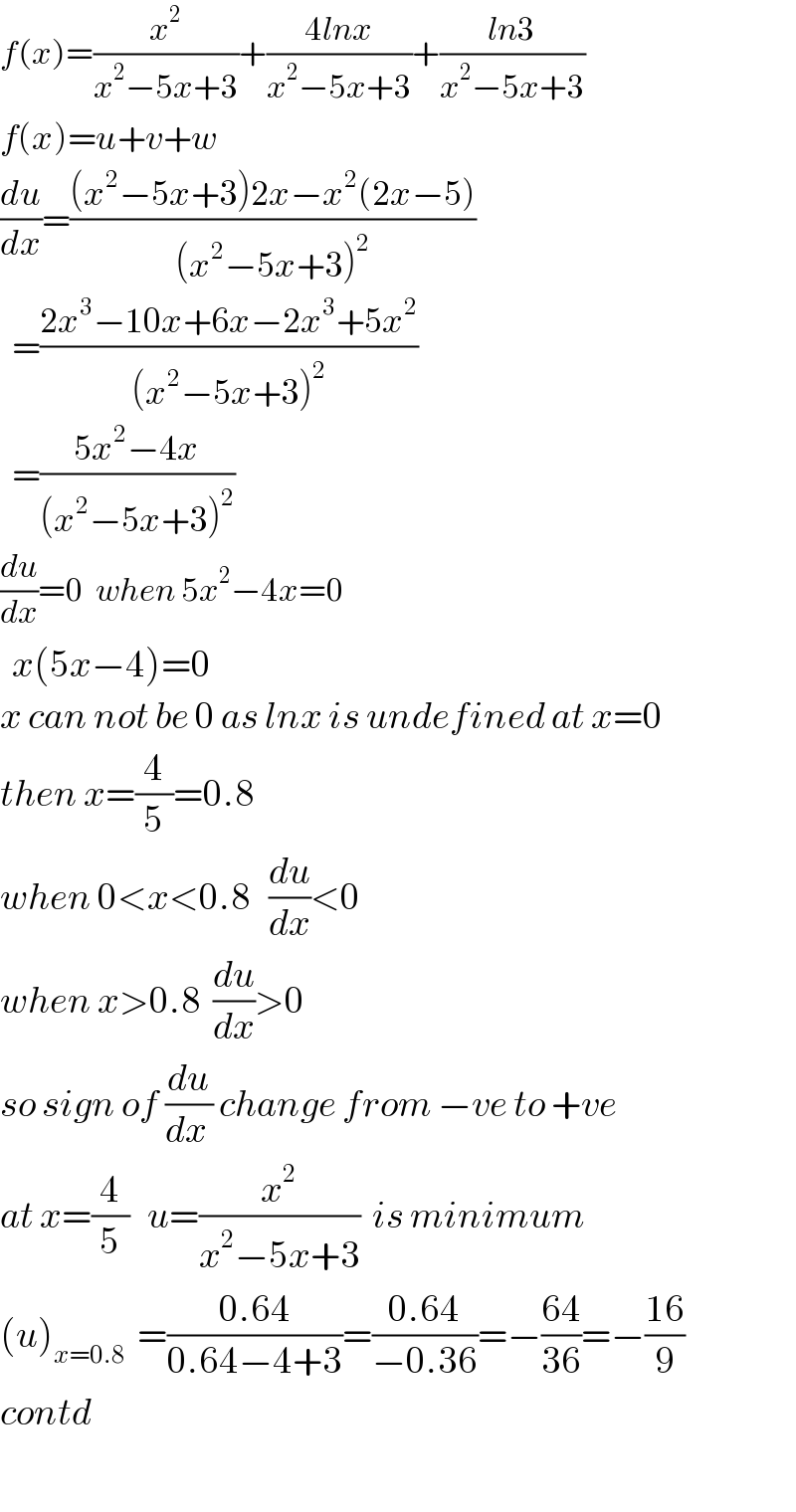
f(x)=(x^2 /(x^2 −5x+3))+((4lnx)/(x^2 −5x+3))+((ln3)/(x^2 −5x+3)) f(x)=u+v+w (du/dx)=(((x^2 −5x+3)2x−x^2 (2x−5))/((x^2 −5x+3)^2 )) =((2x^3 −10x+6x−2x^3 +5x^2 )/((x^2 −5x+3)^2 )) =((5x^2 −4x)/((x^2 −5x+3)^2 )) (du/dx)=0 when 5x^2 −4x=0 x(5x−4)=0 x can not be 0 as lnx is undefined at x=0 then x=(4/5)=0.8 when 0<x<0.8 (du/dx)<0 when x>0.8 (du/dx)>0 so sign of (du/(dx )) change from −ve to +ve at x=(4/5) u=(x^2 /(x^2 −5x+3)) is minimum (u)_(x=0.8) =((0.64)/(0.64−4+3))=((0.64)/(−0.36))=−((64)/(36))=−((16)/9) contd

$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}+\frac{\mathrm{4}{lnx}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}+\frac{{ln}\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}} \\ $$$${f}\left({x}\right)={u}+{v}+{w} \\ $$$$\frac{{du}}{{dx}}=\frac{\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}\right)\mathrm{2}{x}−{x}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{5}\right)}{\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{2}{x}^{\mathrm{3}} −\mathrm{10}{x}+\mathrm{6}{x}−\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}}{\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\frac{{du}}{{dx}}=\mathrm{0}\:\:{when}\:\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}=\mathrm{0} \\ $$$$\:\:{x}\left(\mathrm{5}{x}−\mathrm{4}\right)=\mathrm{0}\: \\ $$$${x}\:{can}\:{not}\:{be}\:\mathrm{0}\:{as}\:{lnx}\:{is}\:{undefined}\:{at}\:{x}=\mathrm{0} \\ $$$${then}\:{x}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{0}.\mathrm{8} \\ $$$${when}\:\mathrm{0}<{x}<\mathrm{0}.\mathrm{8}\:\:\:\frac{{du}}{{dx}}<\mathrm{0}\:\:\: \\ $$$${when}\:{x}>\mathrm{0}.\mathrm{8}\:\:\frac{{du}}{{dx}}>\mathrm{0}\: \\ $$$${so}\:{sign}\:{of}\:\frac{{du}}{{dx}\:}\:{change}\:{from}\:−{ve}\:{to}\:+{ve} \\ $$$${at}\:{x}=\frac{\mathrm{4}}{\mathrm{5}}\:\:\:{u}=\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}}\:\:{is}\:{minimum} \\ $$$$\left({u}\right)_{{x}=\mathrm{0}.\mathrm{8}} \:\:=\frac{\mathrm{0}.\mathrm{64}}{\mathrm{0}.\mathrm{64}−\mathrm{4}+\mathrm{3}}=\frac{\mathrm{0}.\mathrm{64}}{−\mathrm{0}.\mathrm{36}}=−\frac{\mathrm{64}}{\mathrm{36}}=−\frac{\mathrm{16}}{\mathrm{9}} \\ $$$${contd} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply