Question Number 41434 by rahul 19 last updated on 07/Aug/18
Commented by rahul 19 last updated on 07/Aug/18

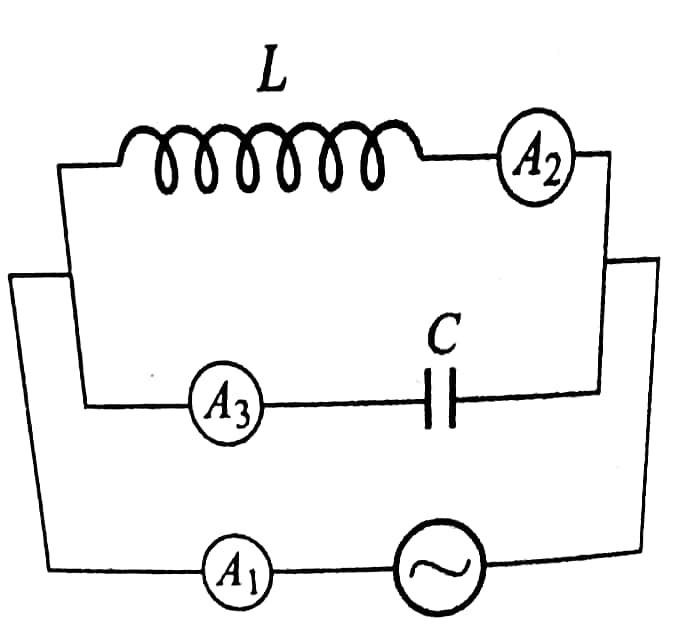
$$\mathrm{If}\:\mathrm{the}\:\mathrm{ammeter}\:\mathrm{A}_{\mathrm{2}\:} \:\mathrm{reads}\:\mathrm{1}.\mathrm{6A}\:\mathrm{and} \\ $$$$\mathrm{ammeter}\:\mathrm{A}_{\mathrm{3}} \:\mathrm{reads}\:\mathrm{0}.\mathrm{4}\:\mathrm{A}\:. \\ $$$$\mathrm{Find}\:\mathrm{reading}\:\mathrm{of}\:\mathrm{ammeter}\:\mathrm{A}_{\mathrm{1}} \:? \\ $$
Answered by ajfour last updated on 07/Aug/18
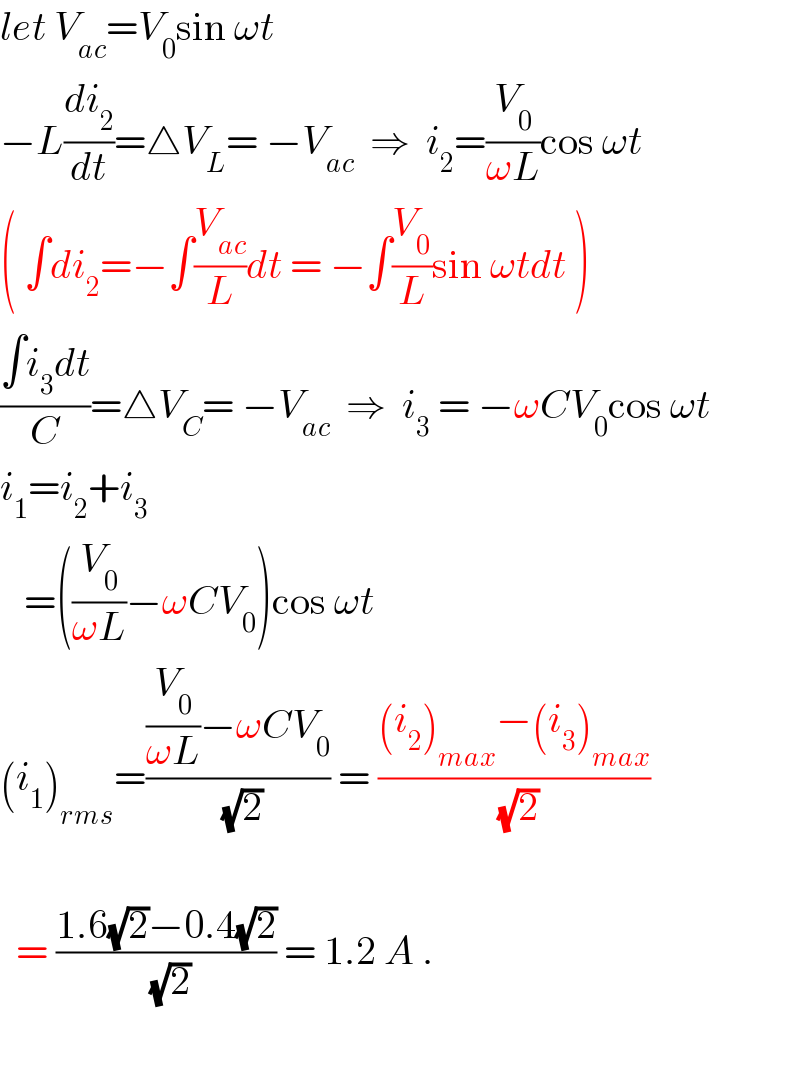
$${let}\:{V}_{{ac}} ={V}_{\mathrm{0}} \mathrm{sin}\:\omega{t} \\ $$$$−{L}\frac{{di}_{\mathrm{2}} }{{dt}}=\bigtriangleup{V}_{{L}} =\:−{V}_{{ac}} \:\:\Rightarrow\:\:{i}_{\mathrm{2}} =\frac{{V}_{\mathrm{0}} }{\omega{L}}\mathrm{cos}\:\omega{t} \\ $$$$\left(\:\int{di}_{\mathrm{2}} =−\int\frac{{V}_{{ac}} }{{L}}{dt}\:=\:−\int\frac{{V}_{\mathrm{0}} }{{L}}\mathrm{sin}\:\omega{tdt}\:\right) \\ $$$$\frac{\int{i}_{\mathrm{3}} {dt}}{{C}}=\bigtriangleup{V}_{{C}} =\:−{V}_{{ac}} \:\:\Rightarrow\:\:{i}_{\mathrm{3}} \:=\:−\omega{CV}_{\mathrm{0}} \mathrm{cos}\:\omega{t} \\ $$$${i}_{\mathrm{1}} ={i}_{\mathrm{2}} +{i}_{\mathrm{3}} \\ $$$$\:\:\:=\left(\frac{{V}_{\mathrm{0}} }{\omega{L}}−\omega{CV}_{\mathrm{0}} \right)\mathrm{cos}\:\omega{t} \\ $$$$\left({i}_{\mathrm{1}} \right)_{{rms}} =\frac{\frac{{V}_{\mathrm{0}} }{\omega{L}}−\omega{CV}_{\mathrm{0}} }{\:\sqrt{\mathrm{2}}}\:=\:\frac{\left({i}_{\mathrm{2}} \right)_{{max}} −\left({i}_{\mathrm{3}} \right)_{{max}} }{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\: \\ $$$$\:\:=\:\frac{\mathrm{1}.\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{0}.\mathrm{4}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:=\:\mathrm{1}.\mathrm{2}\:{A}\:. \\ $$$$\: \\ $$
Commented by rahul 19 last updated on 07/Aug/18
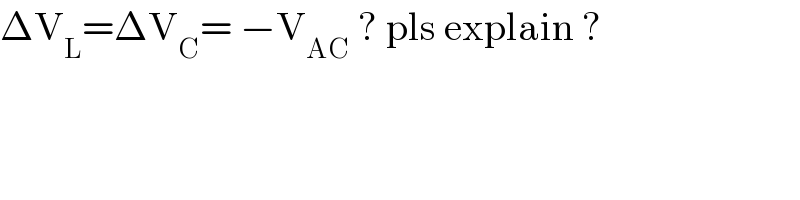
$$\Delta\mathrm{V}_{\mathrm{L}} =\Delta\mathrm{V}_{\mathrm{C}} =\:−\mathrm{V}_{\mathrm{AC}} \:?\:\mathrm{pls}\:\mathrm{explain}\:? \\ $$
Commented by ajfour last updated on 07/Aug/18

$${KVL}\: \\ $$
Commented by ajfour last updated on 07/Aug/18
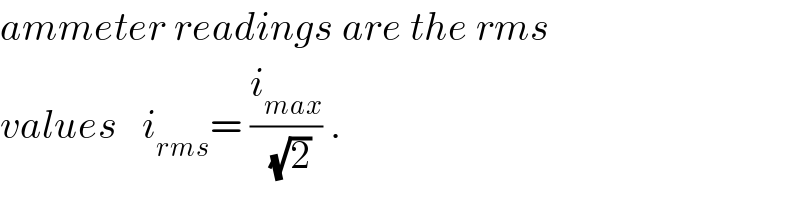
$${ammeter}\:{readings}\:{are}\:{the}\:{rms} \\ $$$${values}\:\:\:{i}_{{rms}} =\:\frac{{i}_{{max}} }{\:\sqrt{\mathrm{2}}}\:. \\ $$
Commented by rahul 19 last updated on 07/Aug/18
Thank you sir!
