Question Number 41620 by Tawa1 last updated on 10/Aug/18

Commented by Tawa1 last updated on 10/Aug/18

$$\mathrm{If}\:\mathrm{each}\:\mathrm{of}\:\mathrm{the}\:\mathrm{small}\:\mathrm{circles}\:\mathrm{in}\:\mathrm{the}\:\mathrm{diagram}\:\mathrm{has}\:\mathrm{the}\:\mathrm{radius}\:=\:\mathrm{r}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{large}\:\mathrm{circle}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{r} \\ $$
Answered by MrW3 last updated on 10/Aug/18
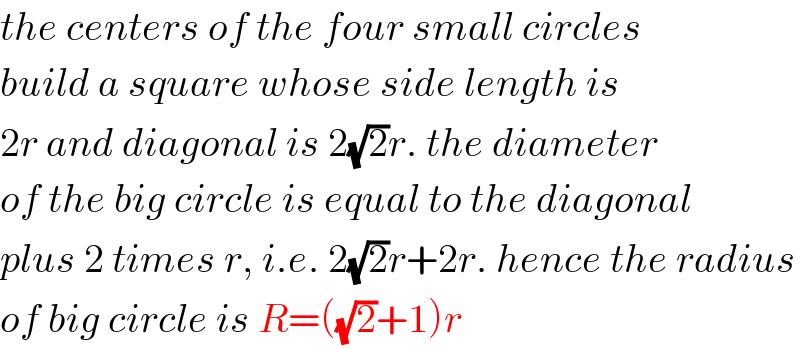
$${the}\:{centers}\:{of}\:{the}\:{four}\:{small}\:{circles} \\ $$$${build}\:{a}\:{square}\:{whose}\:{side}\:{length}\:{is} \\ $$$$\mathrm{2}{r}\:{and}\:{diagonal}\:{is}\:\mathrm{2}\sqrt{\mathrm{2}}{r}.\:{the}\:{diameter} \\ $$$${of}\:{the}\:{big}\:{circle}\:{is}\:{equal}\:{to}\:{the}\:{diagonal} \\ $$$${plus}\:\mathrm{2}\:{times}\:{r},\:{i}.{e}.\:\mathrm{2}\sqrt{\mathrm{2}}{r}+\mathrm{2}{r}.\:{hence}\:{the}\:{radius} \\ $$$${of}\:{big}\:{circle}\:{is}\:{R}=\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){r} \\ $$
Commented by Tawa1 last updated on 10/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18

$$\:{join}\:{the}\:{centres}\:{of}\:{four}\:{circles}…{get}\:{a}\:{square} \\ $$$${side}\:{of}\:{square}=\mathrm{2}{r}\:\: \\ $$$${diagonal}\:{of}\:{square}=\sqrt{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} }\:=\mathrm{2}\sqrt{\mathrm{2}}\:\:{r} \\ $$$${raduis}\:{of}\:{big}\:{circle}\:{is}\:{R} \\ $$$$\mathrm{2}{R}=\mathrm{2}\sqrt{\mathrm{2}}\:\:{r}+\mathrm{2}{r} \\ $$$${R}=\sqrt{\mathrm{2}}\:{r}+{r} \\ $$
Commented by Tawa1 last updated on 10/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
