Question-41675

Question Number 41675 by Raj Singh last updated on 11/Aug/18

Commented by math khazana by abdo last updated on 12/Aug/18

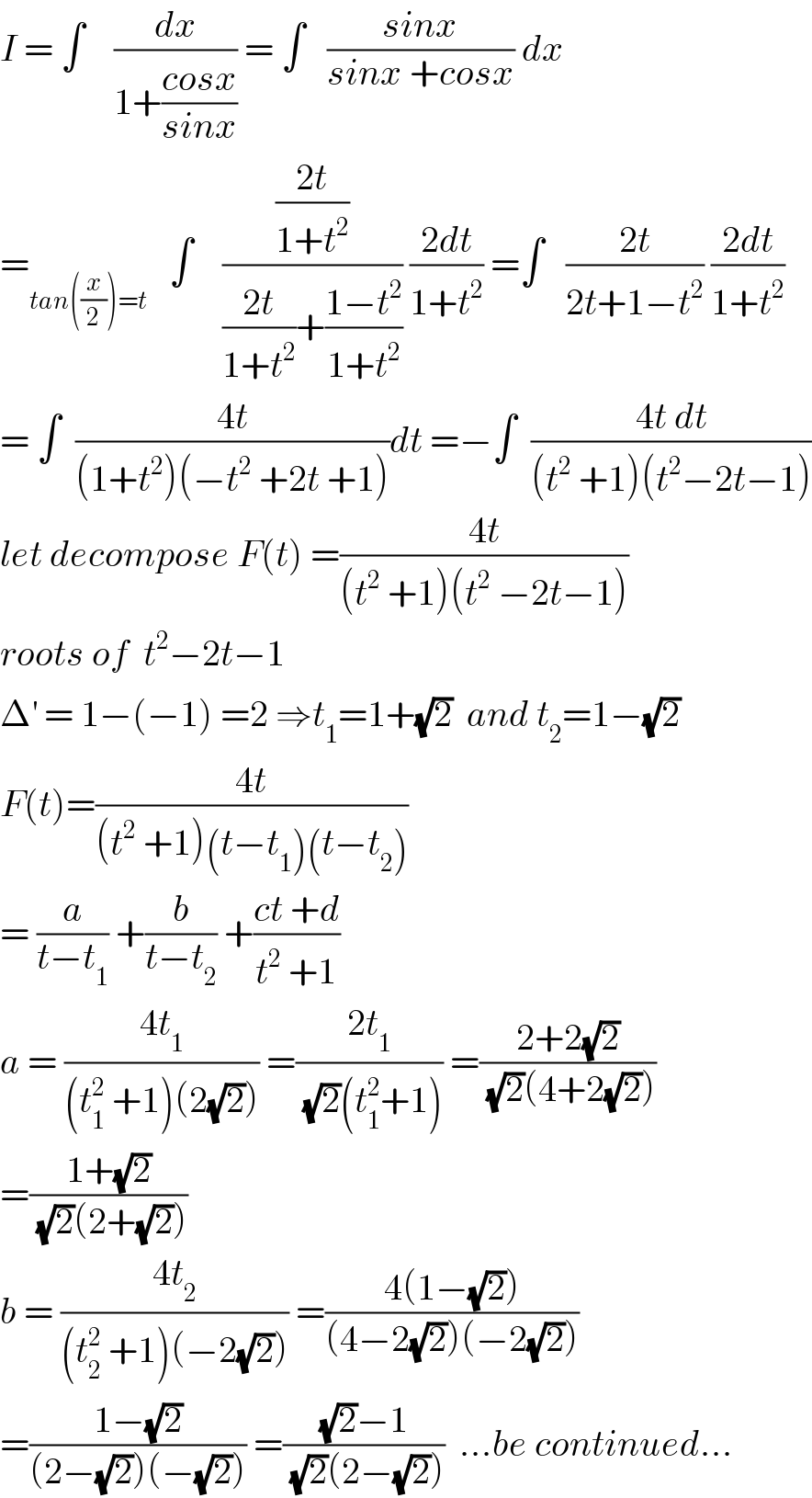
I = ∫ (dx/(1+((cosx)/(sinx)))) = ∫ ((sinx)/(sinx +cosx)) dx =_(tan((x/2))=t) ∫ (((2t)/(1+t^2 ))/(((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫ ((2t)/(2t+1−t^2 )) ((2dt)/(1+t^2 )) = ∫ ((4t)/((1+t^2 )(−t^2 +2t +1)))dt =−∫ ((4t dt)/((t^2 +1)(t^2 −2t−1))) let decompose F(t) =((4t)/((t^2 +1)(t^2 −2t−1))) roots of t^2 −2t−1 Δ^′ = 1−(−1) =2 ⇒t_1 =1+(√2) and t_2 =1−(√2) F(t)=((4t)/((t^2 +1)(t−t_1 )(t−t_2 ))) = (a/(t−t_1 )) +(b/(t−t_2 )) +((ct +d)/(t^2 +1)) a = ((4t_1 )/((t_1 ^2 +1)(2(√2)))) =((2t_1 )/( (√2)(t_1 ^2 +1))) =((2+2(√2))/( (√2)(4+2(√2)))) =((1+(√2))/( (√2)(2+(√2)))) b = ((4t_2 )/((t_2 ^2 +1)(−2(√2)))) =((4(1−(√2)))/((4−2(√2))(−2(√2)))) =((1−(√2))/((2−(√2))(−(√2)))) =(((√2)−1)/( (√2)(2−(√2)))) ...be continued...

$${I}\:=\:\int\:\:\:\:\frac{{dx}}{\mathrm{1}+\frac{{cosx}}{{sinx}}}\:=\:\int\:\:\:\frac{{sinx}}{{sinx}\:+{cosx}}\:{dx} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int\:\:\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{2}{t}}{\mathrm{2}{t}+\mathrm{1}−{t}^{\mathrm{2}} }\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\frac{\mathrm{4}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(−{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{1}\right)}{dt}\:=−\int\:\:\frac{\mathrm{4}{t}\:{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:−\mathrm{2}{t}−\mathrm{1}\right)} \\ $$$${roots}\:{of}\:\:{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1} \\ $$$$\Delta^{'} \:=\:\mathrm{1}−\left(−\mathrm{1}\right)\:=\mathrm{2}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$${F}\left({t}\right)=\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)} \\ $$$$=\:\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\:\frac{\mathrm{4}{t}_{\mathrm{1}} }{\left({t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{2}{t}_{\mathrm{1}} }{\:\sqrt{\mathrm{2}}\left({t}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)} \\ $$$${b}\:=\:\frac{\mathrm{4}{t}_{\mathrm{2}} }{\left({t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)}{\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(−\sqrt{\mathrm{2}}\right)}\:=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}\:\:…{be}\:{continued}… \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18

∫(dx/(1+cotx)) ∫((sinx)/(sinx+cosx))dx =(1/2)∫((cosx+sinx−(cosx−sinx))/(sinx+cosx))dx =(1/2)[∫dx−∫((cosx−sinx)/(sinx+cosx))dx =(1/2)[∫dx−∫((d(sinx+cosx))/(sinx+cosx))] =(1/2)[x−ln(sinx+cosx)]+c

$$\int\frac{{dx}}{\mathrm{1}+{cotx}} \\ $$$$\int\frac{{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cosx}+{sinx}−\left({cosx}−{sinx}\right)}{{sinx}+{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int{dx}−\int\frac{{cosx}−{sinx}}{{sinx}+{cosx}}{dx}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\int{dx}−\int\frac{{d}\left({sinx}+{cosx}\right)}{{sinx}+{cosx}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}−{ln}\left({sinx}+{cosx}\right)\right]+{c} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply