Question Number 41686 by ajfour last updated on 11/Aug/18
Commented by ajfour last updated on 11/Aug/18
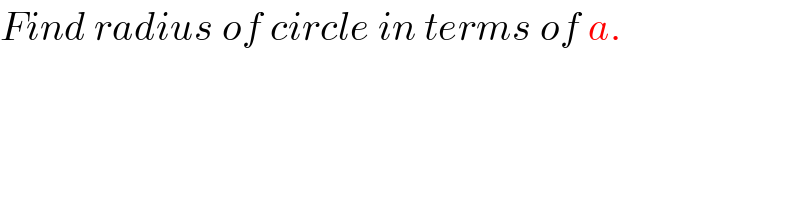
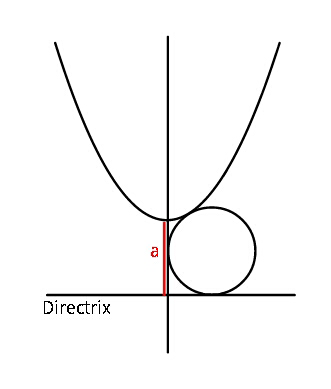
$${Find}\:{radius}\:{of}\:{circle}\:{in}\:{terms}\:{of}\:{a}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18

$${wait}\:\:{pls}… \\ $$
Answered by ajfour last updated on 12/Aug/18
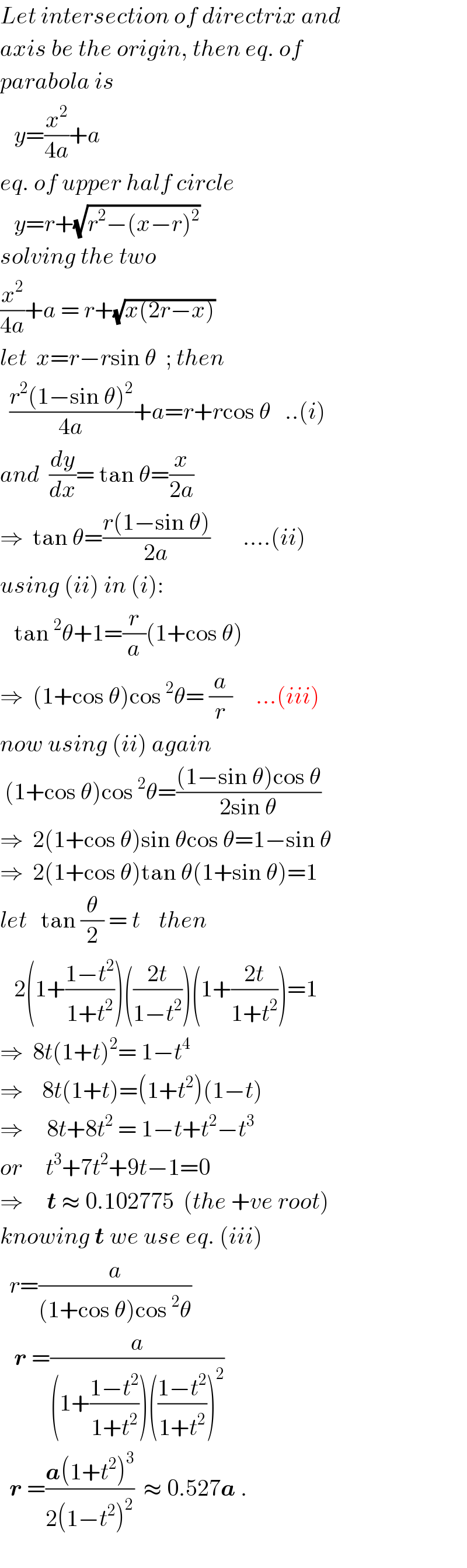
$${Let}\:{intersection}\:{of}\:{directrix}\:{and} \\ $$$${axis}\:{be}\:{the}\:{origin},\:{then}\:{eq}.\:{of} \\ $$$${parabola}\:{is} \\ $$$$\:\:\:{y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}{a}}+{a} \\ $$$${eq}.\:{of}\:{upper}\:{half}\:{circle} \\ $$$$\:\:\:{y}={r}+\sqrt{{r}^{\mathrm{2}} −\left({x}−{r}\right)^{\mathrm{2}} } \\ $$$${solving}\:{the}\:{two} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{4}{a}}+{a}\:=\:{r}+\sqrt{{x}\left(\mathrm{2}{r}−{x}\right)} \\ $$$${let}\:\:{x}={r}−{r}\mathrm{sin}\:\theta\:\:;\:{then} \\ $$$$\:\:\frac{{r}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{\mathrm{4}{a}}+{a}={r}+{r}\mathrm{cos}\:\theta\:\:\:..\left({i}\right) \\ $$$${and}\:\:\frac{{dy}}{{dx}}=\:\mathrm{tan}\:\theta=\frac{{x}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta=\frac{{r}\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}{\mathrm{2}{a}}\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${using}\:\left({ii}\right)\:{in}\:\left({i}\right): \\ $$$$\:\:\:\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{1}=\frac{{r}}{{a}}\left(\mathrm{1}+\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta=\:\frac{{a}}{{r}}\:\:\:\:\:…\left({iii}\right) \\ $$$${now}\:{using}\:\left({ii}\right)\:{again} \\ $$$$\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta=\frac{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\mathrm{2sin}\:\theta} \\ $$$$\Rightarrow\:\:\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta=\mathrm{1}−\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{tan}\:\theta\left(\mathrm{1}+\mathrm{sin}\:\theta\right)=\mathrm{1} \\ $$$${let}\:\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\:=\:{t}\:\:\:\:{then} \\ $$$$\:\:\:\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$$\Rightarrow\:\:\mathrm{8}{t}\left(\mathrm{1}+{t}\right)^{\mathrm{2}} =\:\mathrm{1}−{t}^{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{8}{t}\left(\mathrm{1}+{t}\right)=\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}\right) \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{8}{t}+\mathrm{8}{t}^{\mathrm{2}} \:=\:\mathrm{1}−{t}+{t}^{\mathrm{2}} −{t}^{\mathrm{3}} \\ $$$${or}\:\:\:\:\:{t}^{\mathrm{3}} +\mathrm{7}{t}^{\mathrm{2}} +\mathrm{9}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\boldsymbol{{t}}\:\approx\:\mathrm{0}.\mathrm{102775}\:\:\left({the}\:+{ve}\:{root}\right) \\ $$$${knowing}\:\boldsymbol{{t}}\:{we}\:{use}\:{eq}.\:\left({iii}\right) \\ $$$$\:\:{r}=\frac{{a}}{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:\boldsymbol{{r}}\:=\frac{{a}}{\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$\:\:\boldsymbol{{r}}\:=\frac{\boldsymbol{{a}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} }{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\approx\:\mathrm{0}.\mathrm{527}\boldsymbol{{a}}\:. \\ $$$$ \\ $$
