Question-41957

Question Number 41957 by behi83417@gmail.com last updated on 15/Aug/18

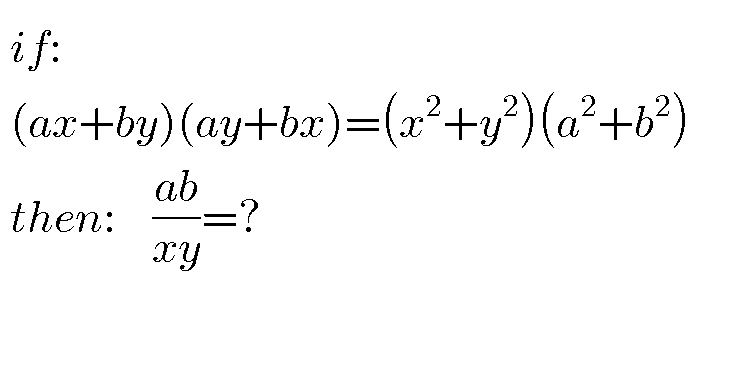
Commented by MJS last updated on 16/Aug/18

I don′t see any solution with all variables ∈R in C we can freely choose 3 variables and solve for the remaining, so there′s no unique solution

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:\mathrm{any}\:\mathrm{solution}\:\mathrm{with}\:\mathrm{all}\:\mathrm{variables}\:\in\mathbb{R} \\ $$$$\mathrm{in}\:\mathbb{C}\:\mathrm{we}\:\mathrm{can}\:\mathrm{freely}\:\mathrm{choose}\:\mathrm{3}\:\mathrm{variables}\:\mathrm{and}\:\mathrm{solve} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{remaining},\:\mathrm{so}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{solution} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18

((ax+by)/2)≥(√(axby)) ((ay+bx)/2)≥(√(aybx)) (ax+by)((ay+bx)≥4abxy so (x^2 +y^2 )(a^2 +b^2 )≥4abxy x^2 a^2 +x^2 b^2 +a^2 y^2 +b^2 y^2 −4abxy≥0 (ax−by)^2 +((ay−bx)^2 ≥0 if consider (ax−by)^2 +(ay−bx)^2 =0 then ax=by (a/y)=(b/x)=r a=ry b=rx ay=bx ry^2 =rx^2 r(x^2 −y^2 )=0 so x=y x=y hencea=ry b=rx=ry so a=b a=b (ax+by)(ay+bx)=(x^2 +y^2 )(a^2 +b^2 ) (ax+ax)(ax+ax)=(x^2 +x^2 )(a^2 +a^2 ) 4a^2 x^2 =4x^2 a^2 co relation between ab and xy can not be established to find ((ab)/(xy))

$$\frac{{ax}+{by}}{\mathrm{2}}\geqslant\sqrt{{axby}}\: \\ $$$$\frac{{ay}+{bx}}{\mathrm{2}}\geqslant\sqrt{{aybx}}\: \\ $$$$\left({ax}+{by}\right)\left(\left({ay}+{bx}\right)\geqslant\mathrm{4}{abxy}\right. \\ $$$${so} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\geqslant\mathrm{4}{abxy} \\ $$$${x}^{\mathrm{2}} {a}^{\mathrm{2}} +{x}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} +{b}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{4}{abxy}\geqslant\mathrm{0} \\ $$$$\left({ax}−{by}\right)^{\mathrm{2}} +\left(\left({ay}−{bx}\right)^{\mathrm{2}} \geqslant\mathrm{0}\right. \\ $$$${if}\:\:{consider} \\ $$$$\left({ax}−{by}\right)^{\mathrm{2}} +\left({ay}−{bx}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${then}\:{ax}={by} \\ $$$$\frac{{a}}{{y}}=\frac{{b}}{{x}}={r} \\ $$$${a}={ry}\:\:\:{b}={rx} \\ $$$${ay}={bx} \\ $$$${ry}^{\mathrm{2}} ={rx}^{\mathrm{2}} \\ $$$${r}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${so}\:{x}={y}\:\:{x}={y} \\ $$$${hencea}={ry} \\ $$$${b}={rx}={ry} \\ $$$${so}\:{a}={b}\:\:{a}={b} \\ $$$$\left({ax}+{by}\right)\left({ay}+{bx}\right)=\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\left({ax}+{ax}\right)\left({ax}+{ax}\right)=\left({x}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +{a}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} {a}^{\mathrm{2}} \\ $$$${co}\:{relation}\:{between}\:{ab}\:{and}\:{xy}\:{can}\:{not}\:{be}\:{established} \\ $$$$ \\ $$$${to}\:{find}\:\:\frac{{ab}}{{xy}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply