Menu Close

Question-41989

Tinku Tara 0 Comments
Pin




Question Number 41989 by Raj Singh last updated on 16/Aug/18
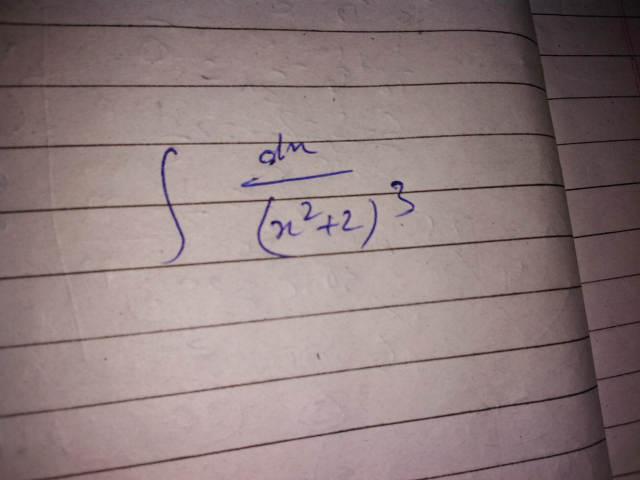
Commented by maxmathsup by imad last updated on 16/Aug/18
let I = ∫ (dx/((x^2 +2)^3 )) changement x=(√2)tan(t) give I = ∫ (((√2)(1+tan^2 t))/(8(1+tan^2 t)^3 ))dt =((√2)/8) ∫ cos^4 t dt =((√2)/8) ∫ (((1+cos(2t))/2))^2 dt =((√2)/(32)) ∫ (1+2cos(2t) +cos^2 (2t))dt =((√2)/(32)) t +((√2)/(16)) ∫ cos(2t)dt +((√2)/(64)) ∫ (1+cos(4t))dt =((√2)/(32))t +((√2)/(32)) sin(2t) +((√2)/(64))t +((√2)/(4×64)) sin(4t) =((3(√2))/(32)) t +((√2)/(32)) sin(2t) +((√2)/(256)) sin(4t) but t =arctan((x/( (√2)))) sin(2t) =((2tan(t))/(1+tan^2 t)) =((2(x/( (√2))))/(1+((x/( (√2))))^2 )) =((2x(√2))/(2+x^2 )) sin(4t) =2sin(2t)cos(2t) =((4tan(t))/(1+tan^2 (t))) ((1−tan^2 (t))/(1+tan^2 t)) =((4(x/( (√2)))(1−((x/( (√2))))^2 ))/((1+((x/( (√2))))^2 )^2 )) = ((((4x)/( (√2)))(((2−x^2 )/2)))/((((2+x^2 )/2))^2 )) = 4 .(4/(2(√2))) ((2−x^2 )/((2+x^2 )^2 )) =(8/( (√2))) ((2−x^2 )/((2+x^2 )^2 )) ⇒ I =((3(√2))/(32)) arctan((x/( (√2)))) +((√2)/(32)) ((2x(√2))/(2+x^2 )) +((√2)/(256)) (8/( (√2))) ((2−x^2 )/((2+x^2 )^2 )) +c .
$${let}\:\:{I}\:\:=\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)^{\mathrm{3}} }\:\:{changement}\:{x}=\sqrt{\mathrm{2}}{tan}\left({t}\right)\:{give} \\ $$$${I}\:\:=\:\int\:\:\:\:\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)}{\mathrm{8}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\mathrm{3}} }{dt}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\:\int\:\:\:{cos}^{\mathrm{4}} {t}\:{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\int\:\:\:\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right)^{\mathrm{2}} {dt}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:\:\int\:\:\:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:{t}\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\:\int\:\:\:{cos}\left(\mathrm{2}{t}\right){dt}\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}\:\int\:\:\:\left(\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)\right){dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}{t}\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:{sin}\left(\mathrm{2}{t}\right)\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{64}}{t}\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}×\mathrm{64}}\:{sin}\left(\mathrm{4}{t}\right) \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\:{t}\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:{sin}\left(\mathrm{2}{t}\right)\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{256}}\:{sin}\left(\mathrm{4}{t}\right)\:\:{but}\:\:\:{t}\:={arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${sin}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{2}{tan}\left({t}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\:\:=\frac{\mathrm{2}\frac{{x}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{x}\sqrt{\mathrm{2}}}{\mathrm{2}+{x}^{\mathrm{2}} } \\ $$$${sin}\left(\mathrm{4}{t}\right)\:=\mathrm{2}{sin}\left(\mathrm{2}{t}\right){cos}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{4}{tan}\left({t}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left({t}\right)}\:\frac{\mathrm{1}−{tan}^{\mathrm{2}} \left({t}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} {t}} \\ $$$$=\frac{\mathrm{4}\frac{{x}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}−\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right)}{\left(\mathrm{1}+\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\frac{\frac{\mathrm{4}{x}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\left(\frac{\mathrm{2}+{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }\:=\:\mathrm{4}\:.\frac{\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{8}}{\:\sqrt{\mathrm{2}}}\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:\:=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\:{arctan}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{32}}\:\frac{\mathrm{2}{x}\sqrt{\mathrm{2}}}{\mathrm{2}+{x}^{\mathrm{2}} }\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{256}}\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{2}}}\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:+{c}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Aug/18
x=(√2) tanα dx=(√2) sec^2 α dα ∫(((√2) sec^2 αdα)/({2(tan^2 α +1)}^3 )) (((√2) )/2^3 )∫((sec^2 α)/(sec^6 α))dα (1/(4(√2)))∫cos^4 αdα (1/(4(√2)))∫((1+cos2α)/2)×((1+cos2α)/2)dα (1/(16(√2) ))∫1+2cos2α+((1+cos4α)/2) dα (1/(16(√2) ))∫dα+(1/(8(√2) ))∫cos2α+(1/(32(√2)))∫dα+(1/(32(√2)))∫cos4αdα =(1/(16(√2)))α+(1/(8(√2)))×((sin2α)/2)+(1/(32(√2)))α+(1/(32(√2)))×((sin4α)/4)+c =(1/(32(√2) ))(2α+α)+(1/(16(√(2 ))))×((2tanα)/(1+tan^2 α))+(1/(128(√2)))×(2.((2tanα)/(1+tan^2 α)).((1−tan^2 α)/(1+tan^2 α))) =(1/(32(√2)))×3tan^(−1) ((x/( (√2))))+(1/(8(√2)))×((x/( (√2)))/(1+(x^2 /2)))+(1/(32(√2)))(((x/( (√2)))/(1+(x^2 /2))).((1−(x^2 /2))/(1+(x^2 /2)))) =(1/(32(√2)))×3tan^(−1) ((x/( (√2))))+(1/(8(√2)))×(2/( (√2)))×(x/(2+x^2 ))+(1/(32(√2)))((√2) .(x/(2+x^2 )).((2−x^2 )/(2+x^2 ))) =(1/(32(√2)))×3tan^(−1) ((x/( (√2) )))+(1/8).(x/(2+x^2 ))+(1/(32)){((x.(2−x^2 ))/((2+x^2 )^2 ))} =(3/(32(√2)))tan^(−1) ((x/( (√2))))+(1/8).(x/(2+x^2 )).(1+(1/4).((2−x^2 )/(2+x^2 ))) =((3(√2))/(64))tan^(−1) (((x(√2))/2))+(1/8).(x/(2+x^2 ))(((8+4x^2 +2−x^2 )/(8+4x^2 ))) =((3(√2))/(64))tan^(−1) (((x(√2))/2))+(1/8).(x/(2+x^2 )).(((10+3x^2 )/(8+4x^2 ))) ((3(√2))/(64))tan^(−1) (((x(√2))/2))+((x(10+3x^2 ))/((16+8x^2 )(8+4x^2 )))
$${x}=\sqrt{\mathrm{2}}\:{tan}\alpha\:\:{dx}=\sqrt{\mathrm{2}}\:{sec}^{\mathrm{2}} \alpha\:{d}\alpha \\ $$$$\int\frac{\sqrt{\mathrm{2}}\:{sec}^{\mathrm{2}} \alpha{d}\alpha}{\left\{\mathrm{2}\left({tan}^{\mathrm{2}} \alpha\:+\mathrm{1}\right)\right\}^{\mathrm{3}} } \\ $$$$\frac{\sqrt{\mathrm{2}}\:}{\mathrm{2}^{\mathrm{3}} }\int\frac{{sec}^{\mathrm{2}} \alpha}{{sec}^{\mathrm{6}} \alpha}{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int{cos}^{\mathrm{4}} \alpha{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}+{cos}\mathrm{2}\alpha}{\mathrm{2}}×\frac{\mathrm{1}+{cos}\mathrm{2}\alpha}{\mathrm{2}}{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}\:}\int\mathrm{1}+\mathrm{2}{cos}\mathrm{2}\alpha+\frac{\mathrm{1}+{cos}\mathrm{4}\alpha}{\mathrm{2}}\:{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}\:}\int{d}\alpha+\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:}\int{cos}\mathrm{2}\alpha+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\int{d}\alpha+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\int{cos}\mathrm{4}\alpha{d}\alpha \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}}\alpha+\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}×\frac{{sin}\mathrm{2}\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\alpha+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}×\frac{{sin}\mathrm{4}\alpha}{\mathrm{4}}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}\:}\left(\mathrm{2}\alpha+\alpha\right)+\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}\:}}×\frac{\mathrm{2}{tan}\alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}+\frac{\mathrm{1}}{\mathrm{128}\sqrt{\mathrm{2}}}×\left(\mathrm{2}.\frac{\mathrm{2}{tan}\alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}.\frac{\mathrm{1}−{tan}^{\mathrm{2}} \alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}×\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}×\frac{\frac{{x}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\left(\frac{\frac{{x}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}.\frac{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}×\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}×\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}\:.\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }.\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{2}+{x}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}\sqrt{\mathrm{2}}}×\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}\:}\right)+\frac{\mathrm{1}}{\mathrm{8}}.\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{32}}\left\{\frac{{x}.\left(\mathrm{2}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{2}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{32}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{8}}.\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }.\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{2}+{x}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}{tan}^{−\mathrm{1}} \left(\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{8}}.\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }\left(\frac{\mathrm{8}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{8}+\mathrm{4}{x}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}{tan}^{−\mathrm{1}} \left(\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{8}}.\frac{{x}}{\mathrm{2}+{x}^{\mathrm{2}} }.\left(\frac{\mathrm{10}+\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{8}+\mathrm{4}{x}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}{tan}^{−\mathrm{1}} \left(\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+\frac{{x}\left(\mathrm{10}+\mathrm{3}{x}^{\mathrm{2}} \right)}{\left(\mathrm{16}+\mathrm{8}{x}^{\mathrm{2}} \right)\left(\mathrm{8}+\mathrm{4}{x}^{\mathrm{2}} \right)} \\ $$
Answered by MJS last updated on 16/Aug/18
reduction formula: ∫(dx/((ax^2 +b)^n ))=(x/(2b(n−1)(ax^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(dx/((ax^2 +b)^(n−1) )) in this case (1) a=1 b=2 n=3 (x/(8(x^2 +2)^2 ))+(3/8)∫(dx/((x^2 +2)^2 )) (2) a=1 b=2 n=2 (x/(8(x^2 +2)^2 ))+((3x)/(32(x^2 +2)))+(3/(32))∫(dx/(x^2 +2)) ∫(dx/(x^2 +c))=((√c)/c)arctan ((x(√c))/c) (x/(8(x^2 +2)^2 ))+((3x)/(32(x^2 +2)))+((3(√2))/(64))arctan ((x(√2))/2) +C ((x(3x^2 +10))/(32(x^2 +2)^2 ))+((3(√2))/(64))arctan ((x(√2))/2) +C
$$\mathrm{reduction}\:\mathrm{formula}: \\ $$$$\int\frac{{dx}}{\left({ax}^{\mathrm{2}} +{b}\right)^{{n}} }=\frac{{x}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }+\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)}\int\frac{{dx}}{\left({ax}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} } \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$$\left(\mathrm{1}\right)\:{a}=\mathrm{1}\:\:{b}=\mathrm{2}\:\:{n}=\mathrm{3} \\ $$$$\frac{{x}}{\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{8}}\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\:{a}=\mathrm{1}\:\:{b}=\mathrm{2}\:\:{n}=\mathrm{2} \\ $$$$\frac{{x}}{\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}{x}}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)}+\frac{\mathrm{3}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} +{c}}=\frac{\sqrt{{c}}}{{c}}\mathrm{arctan}\:\frac{{x}\sqrt{{c}}}{{c}} \\ $$$$\frac{{x}}{\mathrm{8}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}{x}}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{arctan}\:\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\:+{C} \\ $$$$\frac{{x}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{10}\right)}{\mathrm{32}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{64}}\mathrm{arctan}\:\frac{{x}\sqrt{\mathrm{2}}}{\mathrm{2}}\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *