Question Number 42054 by SammyKT last updated on 17/Aug/18
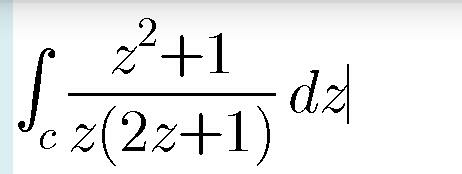
Commented by math khazana by abdo last updated on 17/Aug/18
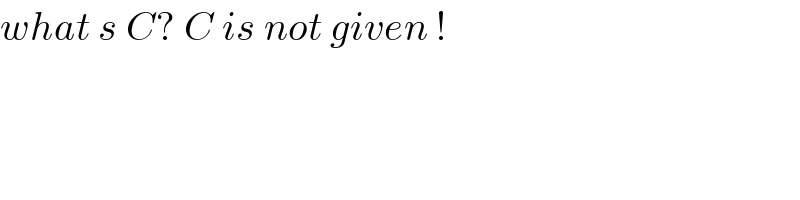
$${what}\:{s}\:{C}?\:{C}\:{is}\:{not}\:{given}\:! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18
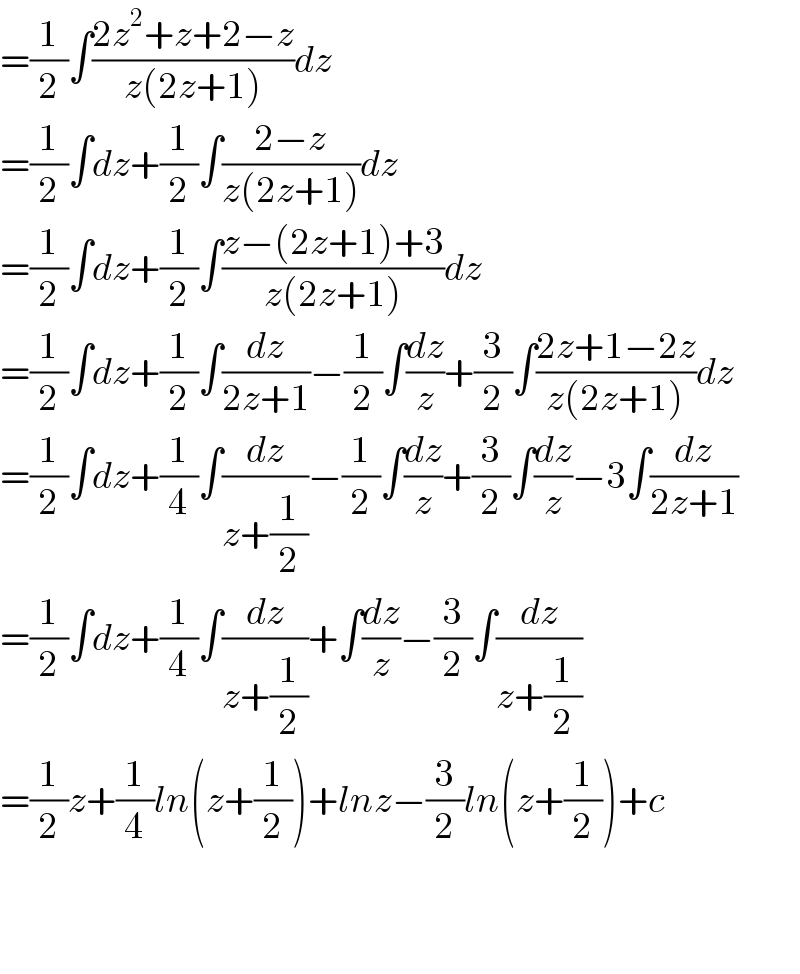
$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{z}^{\mathrm{2}} +{z}+\mathrm{2}−{z}}{{z}\left(\mathrm{2}{z}+\mathrm{1}\right)}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}−{z}}{{z}\left(\mathrm{2}{z}+\mathrm{1}\right)}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{z}−\left(\mathrm{2}{z}+\mathrm{1}\right)+\mathrm{3}}{{z}\left(\mathrm{2}{z}+\mathrm{1}\right)}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dz}}{\mathrm{2}{z}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dz}}{{z}}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}{z}+\mathrm{1}−\mathrm{2}{z}}{{z}\left(\mathrm{2}{z}+\mathrm{1}\right)}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dz}}{{z}+\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dz}}{{z}}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{{z}}−\mathrm{3}\int\frac{{dz}}{\mathrm{2}{z}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dz}}{{z}+\frac{\mathrm{1}}{\mathrm{2}}}+\int\frac{{dz}}{{z}}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{{z}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{z}+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{lnz}−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{c} \\ $$$$ \\ $$$$ \\ $$
Commented by SammyKT last updated on 17/Aug/18

$${Thank}\:{you}\:{sir}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Aug/18

$${itsok}… \\ $$
