Question Number 42331 by AR Akash last updated on 23/Aug/18

Answered by $@ty@m last updated on 23/Aug/18
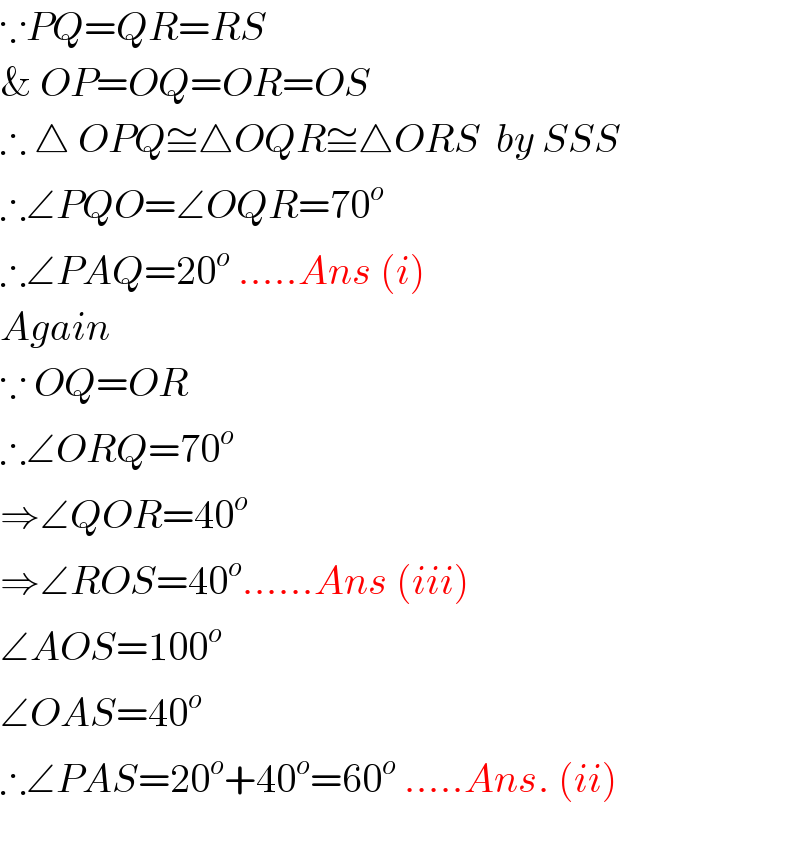
$$\because{PQ}={QR}={RS} \\ $$$$\&\:{OP}={OQ}={OR}={OS} \\ $$$$\therefore\:\bigtriangleup\:{OPQ}\cong\bigtriangleup{OQR}\cong\bigtriangleup{ORS}\:\:{by}\:{SSS} \\ $$$$\therefore\angle{PQO}=\angle{OQR}=\mathrm{70}^{{o}} \\ $$$$\therefore\angle{PAQ}=\mathrm{20}^{{o}} \:…..{Ans}\:\left({i}\right) \\ $$$${Again} \\ $$$$\because\:{OQ}={OR} \\ $$$$\therefore\angle{ORQ}=\mathrm{70}^{{o}} \\ $$$$\Rightarrow\angle{QOR}=\mathrm{40}^{{o}} \\ $$$$\Rightarrow\angle{ROS}=\mathrm{40}^{{o}} ……{Ans}\:\left({iii}\right) \\ $$$$\angle{AOS}=\mathrm{100}^{{o}} \\ $$$$\angle{OAS}=\mathrm{40}^{{o}} \\ $$$$\therefore\angle{PAS}=\mathrm{20}^{{o}} +\mathrm{40}^{{o}} =\mathrm{60}^{{o}} \:…..{Ans}.\:\left({ii}\right) \\ $$$$ \\ $$
Commented by Vashu last updated on 24/Aug/18

$${how}\angle{PAQ}\:{came}\:?{explain} \\ $$
Commented by $@ty@m last updated on 24/Aug/18
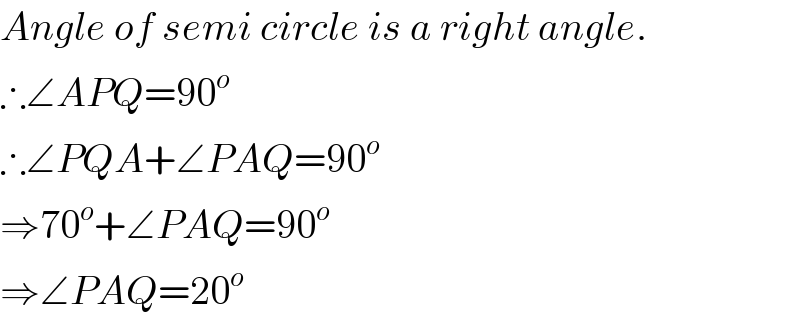
$${Angle}\:{of}\:{semi}\:{circle}\:{is}\:{a}\:{right}\:{angle}. \\ $$$$\therefore\angle{APQ}=\mathrm{90}^{{o}} \\ $$$$\therefore\angle{PQA}+\angle{PAQ}=\mathrm{90}^{{o}} \\ $$$$\Rightarrow\mathrm{70}^{{o}} +\angle{PAQ}=\mathrm{90}^{{o}} \\ $$$$\Rightarrow\angle{PAQ}=\mathrm{20}^{{o}} \\ $$
