Question-42340

Question Number 42340 by ajfour last updated on 23/Aug/18

Commented by ajfour last updated on 23/Aug/18

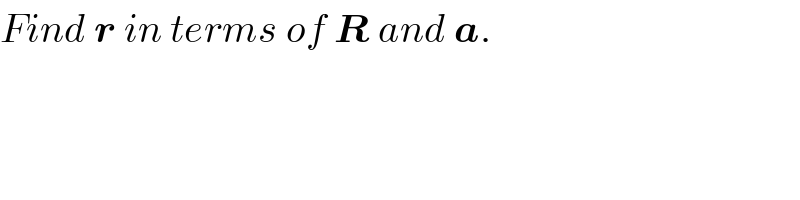
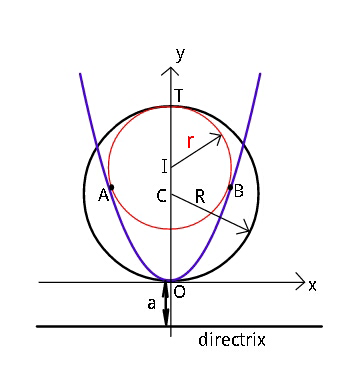
$${Find}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:\boldsymbol{{R}}\:{and}\:\boldsymbol{{a}}. \\ $$

Commented by MJS last updated on 24/Aug/18

sorry I′m on holidays and don′t have internet all the time...

$$\mathrm{sorry}\:\mathrm{I}'\mathrm{m}\:\mathrm{on}\:\mathrm{holidays}\:\mathrm{and}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{internet} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{time}… \\ $$

Commented by ajfour last updated on 25/Aug/18

$${no}\:{problem}\:{sir}\:.\:{enjoy}\:! \\ $$

Answered by ajfour last updated on 25/Aug/18

eq. of parabola y=(x^2 /(4a)) eq. of smaller circle x^2 +(y−2R+r)^2 =r^2 the small circle and parabola have only one common value of x^2 ; hence x^2 +((x^2 /(4a))−2R+r)^2 =r^2 let x^2 =t ; then (t^2 /(16a^2 ))+[1−((2(2R−r))/(4a))]t +2R(2R−2r)=0 for just one value of t ⇒ (([4a−2(2R−r)]^2 )/(16a^2 )) = ((8R(2R−2r))/(16a^2 )) ⇒ 4a^2 +(2R−r)^2 −4a(2R−r) = 4R^2 −4rR ⇒ r^2 +4ar+4a^2 −8aR =0 ⇒ r =−2a+(√(4a^2 −4a^2 +8aR)) ⇒ r = (√(8aR))−2a for r=R R^2 +4a^2 +4aR = 8aR ⇒ R= 2a .

$${eq}.\:{of}\:{parabola}\:\:\:\:{y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$${eq}.\:{of}\:\:{smaller}\:{circle} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\left({y}−\mathrm{2}{R}+{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${the}\:{small}\:{circle}\:{and}\:{parabola} \\ $$$${have}\:{only}\:{one}\:{common}\:{value} \\ $$$${of}\:{x}^{\mathrm{2}} ;\:{hence} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\left(\frac{{x}^{\mathrm{2}} }{\mathrm{4}{a}}−\mathrm{2}{R}+{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\:{let}\:{x}^{\mathrm{2}} ={t}\:\:;\:{then} \\ $$$$\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{16}{a}^{\mathrm{2}} }+\left[\mathrm{1}−\frac{\mathrm{2}\left(\mathrm{2}{R}−{r}\right)}{\mathrm{4}{a}}\right]{t}\:+\mathrm{2}{R}\left(\mathrm{2}{R}−\mathrm{2}{r}\right)=\mathrm{0} \\ $$$${for}\:{just}\:{one}\:{value}\:{of}\:{t} \\ $$$$\Rightarrow\:\frac{\left[\mathrm{4}{a}−\mathrm{2}\left(\mathrm{2}{R}−{r}\right)\right]^{\mathrm{2}} }{\mathrm{16}{a}^{\mathrm{2}} }\:=\:\frac{\mathrm{8}{R}\left(\mathrm{2}{R}−\mathrm{2}{r}\right)}{\mathrm{16}{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{4}{a}^{\mathrm{2}} +\left(\mathrm{2}{R}−{r}\right)^{\mathrm{2}} −\mathrm{4}{a}\left(\mathrm{2}{R}−{r}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{rR} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} +\mathrm{4}{ar}+\mathrm{4}{a}^{\mathrm{2}} −\mathrm{8}{aR}\:\:=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{r}\:=−\mathrm{2}{a}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} +\mathrm{8}{aR}} \\ $$$$\Rightarrow\:\:\:{r}\:=\:\sqrt{\mathrm{8}{aR}}−\mathrm{2}{a} \\ $$$$\:\:\:\:\:{for}\:\:{r}={R} \\ $$$$\:\:\:\:\:\:\:{R}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{aR}\:=\:\mathrm{8}{aR} \\ $$$$\Rightarrow\:\:\:\:\:\:{R}=\:\mathrm{2}{a}\:. \\ $$

Commented by Tawa1 last updated on 25/Aug/18

Do you have your own textbook sir ???. Expecially all those your diagrams. I will love to learn them sir. God bless you sir. You, sir tammy and sir mrW3 are genius. Keep the good work going sir. God bless you sir.

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{your}\:\mathrm{own}\:\mathrm{textbook}\:\mathrm{sir}\:???.\:\:\:\mathrm{Expecially}\:\mathrm{all}\:\mathrm{those}\:\mathrm{your} \\ $$$$\mathrm{diagrams}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{them}\:\mathrm{sir}.\:\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{You},\:\mathrm{sir}\:\mathrm{tammy}\:\mathrm{and}\:\mathrm{sir}\:\mathrm{mrW3}\:\:\mathrm{are}\:\mathrm{genius}.\:\:\mathrm{Keep}\:\mathrm{the}\:\mathrm{good}\:\mathrm{work}\:\mathrm{going}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$

Commented by ajfour last updated on 25/Aug/18

$${self}\:{created}\:{questions} \\ $$$${pertains}\:{to}\:{mixture}\:{of}\:{topics} \\ $$$${including}\:{application}\:{of}\:{deriatives}, \\ $$$${coordinate}\:{geometry},\:{quadratic}, \\ $$$${geometry},\:{and}\:{like}.. \\ $$

Commented by Tawa1 last updated on 25/Aug/18

$$\mathrm{Sir}\:\mathrm{the}\:\mathrm{drawings}\:\mathrm{are}\:\mathrm{what}\:\mathrm{topic}\: \\ $$

Commented by Tawa1 last updated on 25/Aug/18

$$\mathrm{Wow}\:!.\:\mathrm{That}\:\mathrm{is}\:\mathrm{great}\:… \\ $$

Commented by ajfour last updated on 25/Aug/18

you can save my questions from this tinkutara forum (topic-geometry or coordinate geometry).

$${you}\:{can}\:{save}\:{my}\:{questions}\:{from} \\ $$$${this}\:{tinkutara}\:{forum}\:\left({topic}-{geometry}\right. \\ $$$$\left.{or}\:{coordinate}\:{geometry}\right). \\ $$

Commented by Tawa1 last updated on 25/Aug/18

My phone is format, i will start saving from today. And if you can share me some past. i would appreciate it sir

$$\mathrm{My}\:\mathrm{phone}\:\mathrm{is}\:\mathrm{format},\:\mathrm{i}\:\mathrm{will}\:\mathrm{start}\:\mathrm{saving}\:\mathrm{from}\:\mathrm{today}.\:\:\mathrm{And}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{share} \\ $$$$\mathrm{me}\:\mathrm{some}\:\mathrm{past}.\:\mathrm{i}\:\mathrm{would}\:\mathrm{appreciate}\:\mathrm{it}\:\mathrm{sir} \\ $$

Answered by MrW3 last updated on 25/Aug/18

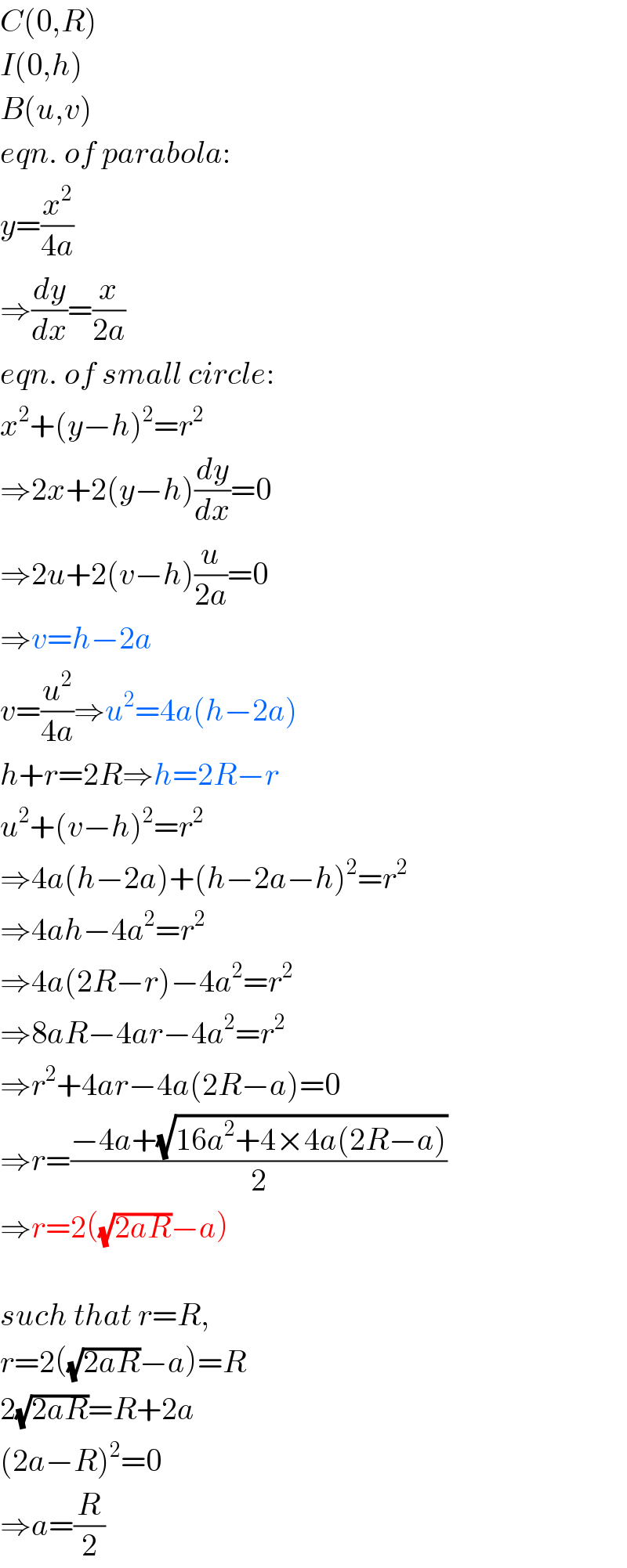
C(0,R) I(0,h) B(u,v) eqn. of parabola: y=(x^2 /(4a)) ⇒(dy/dx)=(x/(2a)) eqn. of small circle: x^2 +(y−h)^2 =r^2 ⇒2x+2(y−h)(dy/dx)=0 ⇒2u+2(v−h)(u/(2a))=0 ⇒v=h−2a v=(u^2 /(4a))⇒u^2 =4a(h−2a) h+r=2R⇒h=2R−r u^2 +(v−h)^2 =r^2 ⇒4a(h−2a)+(h−2a−h)^2 =r^2 ⇒4ah−4a^2 =r^2 ⇒4a(2R−r)−4a^2 =r^2 ⇒8aR−4ar−4a^2 =r^2 ⇒r^2 +4ar−4a(2R−a)=0 ⇒r=((−4a+(√(16a^2 +4×4a(2R−a))))/2) ⇒r=2((√(2aR))−a) such that r=R, r=2((√(2aR))−a)=R 2(√(2aR))=R+2a (2a−R)^2 =0 ⇒a=(R/2)

$${C}\left(\mathrm{0},{R}\right) \\ $$$${I}\left(\mathrm{0},{h}\right) \\ $$$${B}\left({u},{v}\right) \\ $$$${eqn}.\:{of}\:{parabola}: \\ $$$${y}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{{x}}{\mathrm{2}{a}} \\ $$$${eqn}.\:{of}\:{small}\:{circle}: \\ $$$${x}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{2}\left({y}−{h}\right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{u}+\mathrm{2}\left({v}−{h}\right)\frac{{u}}{\mathrm{2}{a}}=\mathrm{0} \\ $$$$\Rightarrow{v}={h}−\mathrm{2}{a} \\ $$$${v}=\frac{{u}^{\mathrm{2}} }{\mathrm{4}{a}}\Rightarrow{u}^{\mathrm{2}} =\mathrm{4}{a}\left({h}−\mathrm{2}{a}\right) \\ $$$${h}+{r}=\mathrm{2}{R}\Rightarrow{h}=\mathrm{2}{R}−{r} \\ $$$${u}^{\mathrm{2}} +\left({v}−{h}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{a}\left({h}−\mathrm{2}{a}\right)+\left({h}−\mathrm{2}{a}−{h}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{ah}−\mathrm{4}{a}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{a}\left(\mathrm{2}{R}−{r}\right)−\mathrm{4}{a}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{8}{aR}−\mathrm{4}{ar}−\mathrm{4}{a}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} +\mathrm{4}{ar}−\mathrm{4}{a}\left(\mathrm{2}{R}−{a}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{−\mathrm{4}{a}+\sqrt{\mathrm{16}{a}^{\mathrm{2}} +\mathrm{4}×\mathrm{4}{a}\left(\mathrm{2}{R}−{a}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\mathrm{2}\left(\sqrt{\mathrm{2}{aR}}−{a}\right) \\ $$$$ \\ $$$${such}\:{that}\:{r}={R}, \\ $$$${r}=\mathrm{2}\left(\sqrt{\mathrm{2}{aR}}−{a}\right)={R} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}{aR}}={R}+\mathrm{2}{a} \\ $$$$\left(\mathrm{2}{a}−{R}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{{R}}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 25/Aug/18

$${thank}\:{you}\:{Sir},\:{too}\:{good}; \\ $$

Commented by Tawa1 last updated on 24/Aug/18

God bless you sir. Sir which topic can i learn diagrams like sir Ajfour always sent

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$$$\mathrm{Sir}\:\mathrm{which}\:\mathrm{topic}\:\mathrm{can}\:\mathrm{i}\:\mathrm{learn}\:\mathrm{diagrams}\:\mathrm{like}\:\mathrm{sir}\:\mathrm{Ajfour}\:\mathrm{always}\:\mathrm{sent} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply