Menu Close

Question-42446

Tinku Tara 0 Comments
Pin




Question Number 42446 by ajfour last updated on 25/Aug/18
Commented by ajfour last updated on 26/Aug/18
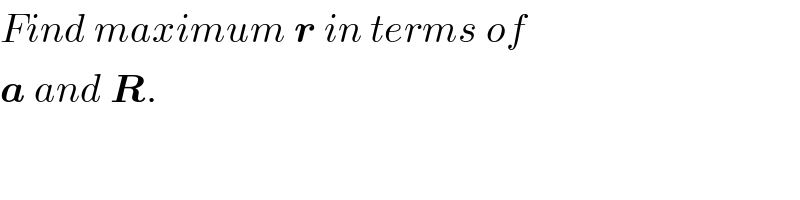
Find maximum r in terms of a and R.
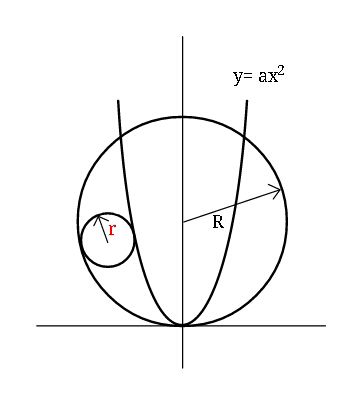
$${Find}\:{maximum}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of} \\ $$$$\boldsymbol{{a}}\:{and}\:\boldsymbol{{R}}.\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Aug/18
solve x^2 +(y−R)^2 =R^2 and y=ax^2 x^2 +y^2 −2yR=0 x^2 +a^2 x^4 −2ax^2 R=0 x^2 (1+a^2 x^2 −2aR)=0 a^2 x^2 =2aR−1 x=((±(√(2aR−1)) )/a) y=ax^2 =a(((2aR−1)/a^2 ))=((2aR−1)/a) point of intersection are (((√(2aR−1))/a),((2aR−1)/a)) and(((−(√(2aR−1)))/a),((2aR−1)/a)) considering+ve side now area between y=ax^2 and x^2 +y^2 −2yR=0 and yaxis say=A remaining area between parabola and circle=B so 2A+2B=ΠR^2 B=((ΠR^2 )/2)−A now area B=Πr^2 +remaining area symetrical w.r.t Πr^2 B=Πr^2 +2S to maximize B contd
$${solve}\:{x}^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:{and}\:{y}={ax}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{yR}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{2}{ax}^{\mathrm{2}} {R}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{aR}\right)=\mathrm{0} \\ $$$${a}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{2}{aR}−\mathrm{1} \\ $$$${x}=\frac{\pm\sqrt{\mathrm{2}{aR}−\mathrm{1}}\:}{{a}} \\ $$$${y}={ax}^{\mathrm{2}} ={a}\left(\frac{\mathrm{2}{aR}−\mathrm{1}}{{a}^{\mathrm{2}} }\right)=\frac{\mathrm{2}{aR}−\mathrm{1}}{{a}} \\ $$$${point}\:{of}\:{intersection}\:{are} \\ $$$$\left(\frac{\sqrt{\mathrm{2}{aR}−\mathrm{1}}}{{a}},\frac{\mathrm{2}{aR}−\mathrm{1}}{{a}}\right)\:{and}\left(\frac{−\sqrt{\mathrm{2}{aR}−\mathrm{1}}}{{a}},\frac{\mathrm{2}{aR}−\mathrm{1}}{{a}}\right) \\ $$$${considering}+{ve}\:{side} \\ $$$${now}\:{area}\:{between}\:{y}={ax}^{\mathrm{2}} \:{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{yR}=\mathrm{0} \\ $$$${and}\:{yaxis}\:{say}={A}\:\:{remaining}\:{area}\:{between}\: \\ $$$${parabola}\:{and}\:{circle}={B} \\ $$$${so}\:\mathrm{2}{A}+\mathrm{2}{B}=\Pi{R}^{\mathrm{2}} \\ $$$${B}=\frac{\Pi{R}^{\mathrm{2}} }{\mathrm{2}}−{A} \\ $$$${now}\:{area}\:{B}=\Pi{r}^{\mathrm{2}} +{remaining}\:{area}\:{symetrical} \\ $$$$\:{w}.{r}.{t}\:\Pi{r}^{\mathrm{2}} \\ $$$${B}=\Pi{r}^{\mathrm{2}} +\mathrm{2}{S} \\ $$$${to}\:{maximize}\:{B} \\ $$$${contd} \\ $$$$ \\ $$
Answered by MJS last updated on 27/Aug/18
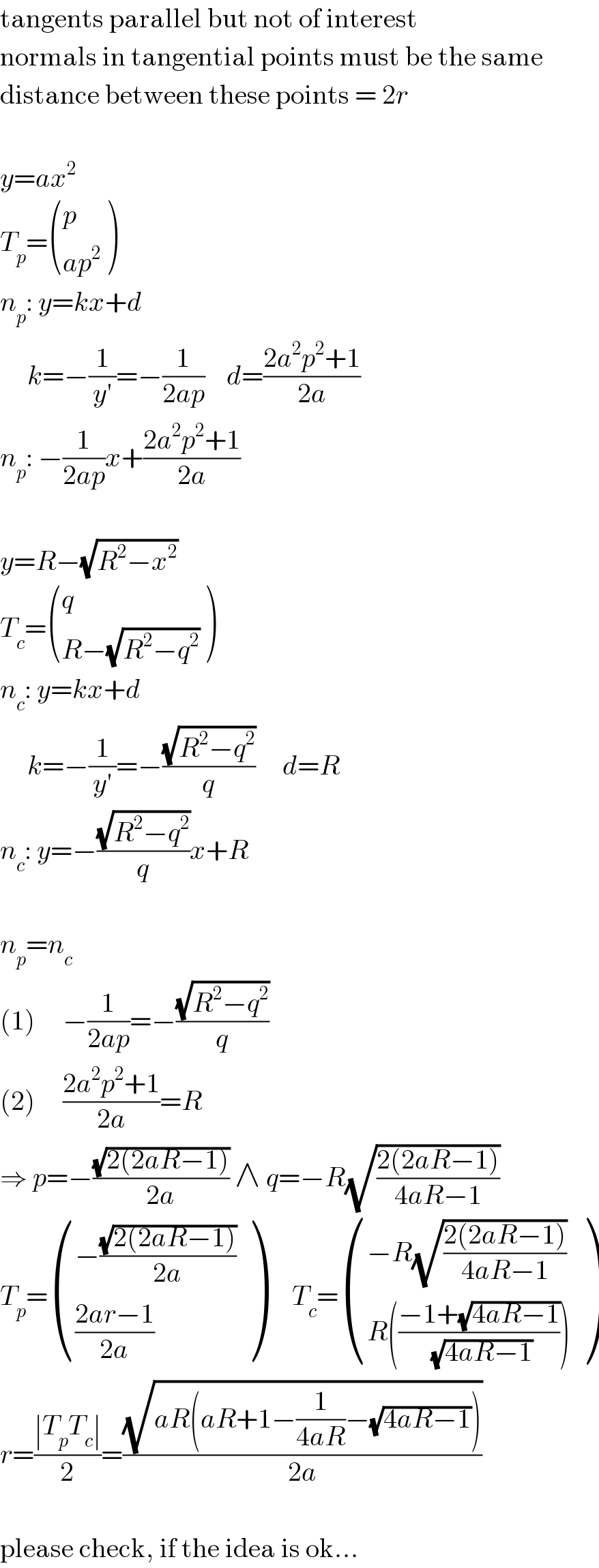
tangents parallel but not of interest normals in tangential points must be the same distance between these points = 2r y=ax^2 T_p = ((p),((ap^2 )) ) n_p : y=kx+d k=−(1/(y′))=−(1/(2ap)) d=((2a^2 p^2 +1)/(2a)) n_p : −(1/(2ap))x+((2a^2 p^2 +1)/(2a)) y=R−(√(R^2 −x^2 )) T_c = ((q),((R−(√(R^2 −q^2 )))) ) n_c : y=kx+d k=−(1/(y′))=−((√(R^2 −q^2 ))/q) d=R n_c : y=−((√(R^2 −q^2 ))/q)x+R n_p =n_c (1) −(1/(2ap))=−((√(R^2 −q^2 ))/q) (2) ((2a^2 p^2 +1)/(2a))=R ⇒ p=−((√(2(2aR−1)))/(2a)) ∧ q=−R(√((2(2aR−1))/(4aR−1))) T_p = (((−((√(2(2aR−1)))/(2a)))),(((2ar−1)/(2a))) ) T_c = (((−R(√((2(2aR−1))/(4aR−1))))),((R(((−1+(√(4aR−1)))/( (√(4aR−1))))))) ) r=((∣T_p T_c ∣)/2)=((√(aR(aR+1−(1/(4aR))−(√(4aR−1)))))/(2a)) please check, if the idea is ok...
$$\mathrm{tangents}\:\mathrm{parallel}\:\mathrm{but}\:\mathrm{not}\:\mathrm{of}\:\mathrm{interest} \\ $$$$\mathrm{normals}\:\mathrm{in}\:\mathrm{tangential}\:\mathrm{points}\:\mathrm{must}\:\mathrm{be}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{distance}\:\mathrm{between}\:\mathrm{these}\:\mathrm{points}\:=\:\mathrm{2}{r} \\ $$$$ \\ $$$${y}={ax}^{\mathrm{2}} \\ $$$${T}_{{p}} =\begin{pmatrix}{{p}}\\{{ap}^{\mathrm{2}} }\end{pmatrix} \\ $$$${n}_{{p}} :\:{y}={kx}+{d} \\ $$$$\:\:\:\:\:{k}=−\frac{\mathrm{1}}{{y}'}=−\frac{\mathrm{1}}{\mathrm{2}{ap}}\:\:\:\:{d}=\frac{\mathrm{2}{a}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$$${n}_{{p}} :\:−\frac{\mathrm{1}}{\mathrm{2}{ap}}{x}+\frac{\mathrm{2}{a}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}} \\ $$$$ \\ $$$${y}={R}−\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${T}_{{c}} =\begin{pmatrix}{{q}}\\{{R}−\sqrt{{R}^{\mathrm{2}} −{q}^{\mathrm{2}} }}\end{pmatrix} \\ $$$${n}_{{c}} :\:{y}={kx}+{d} \\ $$$$\:\:\:\:\:{k}=−\frac{\mathrm{1}}{{y}'}=−\frac{\sqrt{{R}^{\mathrm{2}} −{q}^{\mathrm{2}} }}{{q}}\:\:\:\:\:{d}={R} \\ $$$${n}_{{c}} :\:{y}=−\frac{\sqrt{{R}^{\mathrm{2}} −{q}^{\mathrm{2}} }}{{q}}{x}+{R} \\ $$$$ \\ $$$${n}_{{p}} ={n}_{{c}} \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}{ap}}=−\frac{\sqrt{{R}^{\mathrm{2}} −{q}^{\mathrm{2}} }}{{q}} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\frac{\mathrm{2}{a}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{a}}={R} \\ $$$$\Rightarrow\:{p}=−\frac{\sqrt{\mathrm{2}\left(\mathrm{2}{aR}−\mathrm{1}\right)}}{\mathrm{2}{a}}\:\wedge\:{q}=−{R}\sqrt{\frac{\mathrm{2}\left(\mathrm{2}{aR}−\mathrm{1}\right)}{\mathrm{4}{aR}−\mathrm{1}}} \\ $$$${T}_{{p}} =\begin{pmatrix}{−\frac{\sqrt{\mathrm{2}\left(\mathrm{2}{aR}−\mathrm{1}\right)}}{\mathrm{2}{a}}}\\{\frac{\mathrm{2}{ar}−\mathrm{1}}{\mathrm{2}{a}}}\end{pmatrix}\:\:\:\:\:{T}_{{c}} =\begin{pmatrix}{−{R}\sqrt{\frac{\mathrm{2}\left(\mathrm{2}{aR}−\mathrm{1}\right)}{\mathrm{4}{aR}−\mathrm{1}}}}\\{{R}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{4}{aR}−\mathrm{1}}}{\:\sqrt{\mathrm{4}{aR}−\mathrm{1}}}\right)}\end{pmatrix} \\ $$$${r}=\frac{\mid{T}_{{p}} {T}_{{c}} \mid}{\mathrm{2}}=\frac{\sqrt{{aR}\left({aR}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{aR}}−\sqrt{\mathrm{4}{aR}−\mathrm{1}}\right)}}{\mathrm{2}{a}} \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{check},\:\mathrm{if}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{ok}… \\ $$
Commented by ajfour last updated on 27/Aug/18
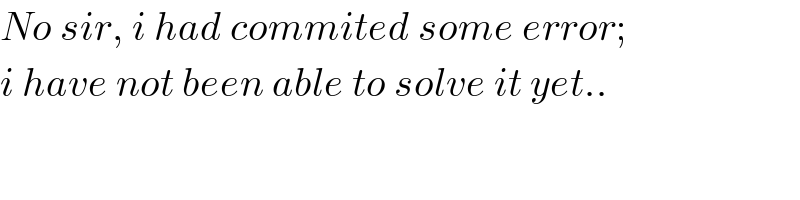
No sir, i had commited some error; i have not been able to solve it yet..
$${No}\:{sir},\:{i}\:{had}\:{commited}\:{some}\:{error}; \\ $$$${i}\:{have}\:{not}\:{been}\:{able}\:{to}\:{solve}\:{it}\:{yet}.. \\ $$
Commented by MJS last updated on 27/Aug/18
ok I′ll check mine...
$$\mathrm{ok}\:\mathrm{I}'\mathrm{ll}\:\mathrm{check}\:\mathrm{mine}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *