Question Number 42448 by Tawa1 last updated on 25/Aug/18

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18

$${y}=\sqrt{\mathrm{3}{x}^{\mathrm{2}} .{y}} \\ $$$${y}=\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{6}{x} \\ $$
Commented by Tawa1 last updated on 25/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{But}\:\mathrm{is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{integrate}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{6x}\:\mathrm{and}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{original}\:\mathrm{question}\:\mathrm{back}\:? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18

$${the}\:{value}\:{of}\:{y}\rightarrow\mathrm{3}{x}^{\mathrm{2}} …. \\ $$$${i}\:{think}\:{it}\:{is}\:{approximation}… \\ $$$${as}\:{y}=\sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} ….\rightarrow\infty}}}} \\ $$$${y}=\sqrt{\mathrm{3}{x}^{\mathrm{2}} ×{y}} \\ $$$${y}^{\mathrm{2}} =\mathrm{3}{x}^{\mathrm{2}} ×{y}\:\:\:\:\:\:{y}=\mathrm{3}{x}^{\mathrm{2}} \\ $$$${supose}\:{you}\:{take}\:{a}\:{glass}\:{of}\:{water}\:{from}\:{ocean} \\ $$$${does}\:{the}\:{quantity}\:{of}\:{water}\:{changes}…{apperently} \\ $$$${no}\:{change}\:{of}\:{volume} \\ $$$${but}\:{truly}\:{speaking}\:{there}\:{is}\:{a}\:{change}\:{of}\:{volume} \\ $$$${v}={v}_{\mathrm{0}} −\bigtriangleup{v} \\ $$$${where}\:\bigtriangleup{v}<<<<<{v} \\ $$$${so}\:{we}\:{consider}\:{v}\approx{v}_{\mathrm{0}} \\ $$$$\int\mathrm{6}{x}\:{dx}=\mathrm{3}{x}^{\mathrm{2}} \:\:+{c} \\ $$
Commented by Tawa1 last updated on 25/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 25/Aug/18
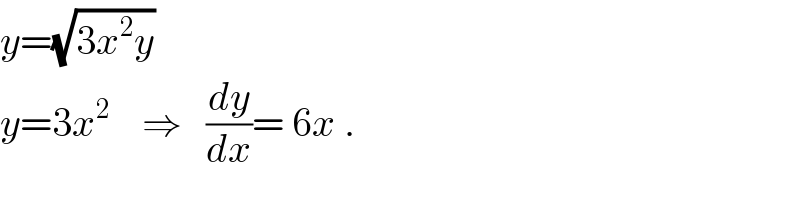
$${y}=\sqrt{\mathrm{3}{x}^{\mathrm{2}} {y}} \\ $$$${y}=\mathrm{3}{x}^{\mathrm{2}} \:\:\:\:\Rightarrow\:\:\:\frac{{dy}}{{dx}}=\:\mathrm{6}{x}\:. \\ $$
Commented by Tawa1 last updated on 25/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by byaw last updated on 25/Aug/18
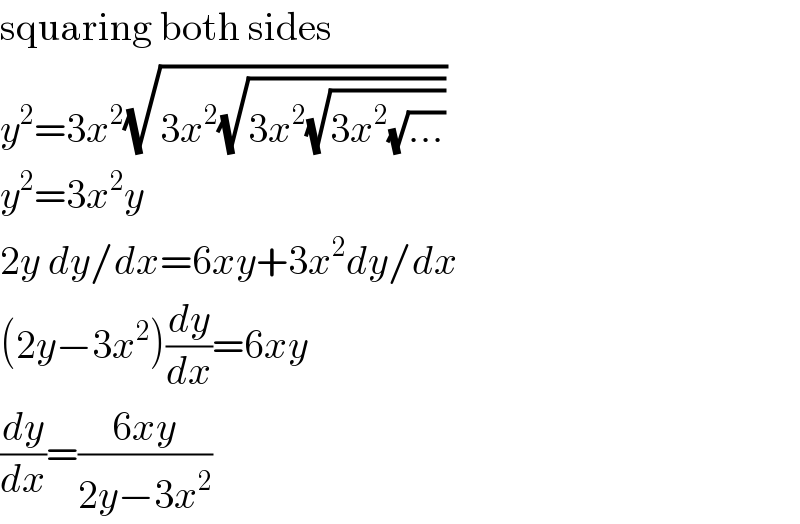
$$\mathrm{squaring}\:\mathrm{both}\:\mathrm{sides} \\ $$$${y}^{\mathrm{2}} =\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{\mathrm{3}{x}^{\mathrm{2}} \sqrt{…}}}} \\ $$$${y}^{\mathrm{2}} =\mathrm{3}{x}^{\mathrm{2}} {y} \\ $$$$\mathrm{2}{y}\:{dy}/{dx}=\mathrm{6}{xy}+\mathrm{3}{x}^{\mathrm{2}} {dy}/{dx} \\ $$$$\left(\mathrm{2}{y}−\mathrm{3}{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}=\mathrm{6}{xy} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{6}{xy}}{\mathrm{2}{y}−\mathrm{3}{x}^{\mathrm{2}} } \\ $$
Commented by Tawa1 last updated on 25/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
