Menu Close

Question-42538

Tinku Tara 0 Comments
Pin




Question Number 42538 by ajfour last updated on 27/Aug/18
Commented by ajfour last updated on 29/Aug/18
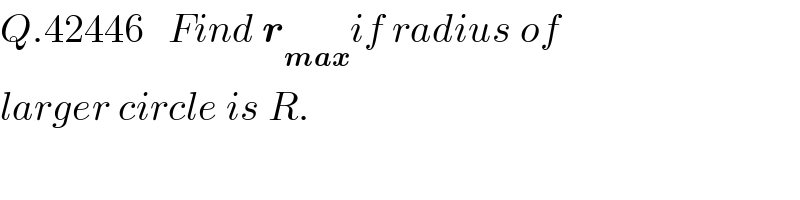
Q.42446 Find r_(max) if radius of larger circle is R.
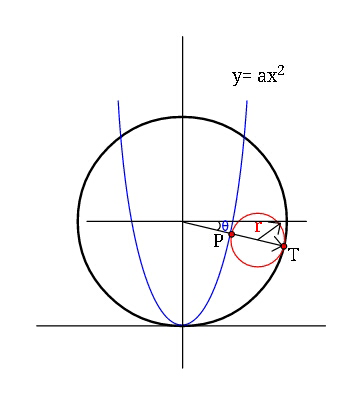
$${Q}.\mathrm{42446}\:\:\:{Find}\:\boldsymbol{{r}}_{\boldsymbol{{max}}} {if}\:{radius}\:{of} \\ $$$${larger}\:{circle}\:{is}\:{R}. \\ $$
Answered by ajfour last updated on 29/Aug/18
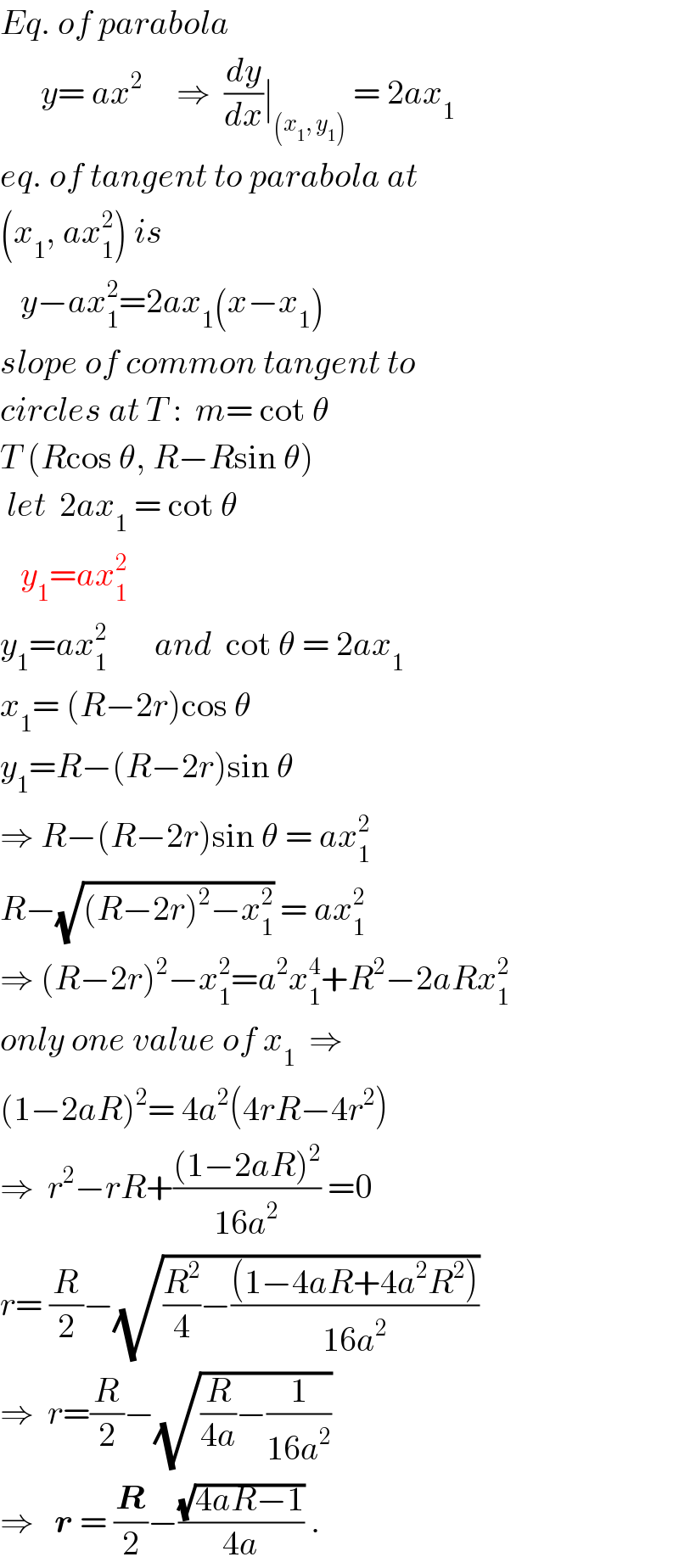
Eq. of parabola y= ax^2 ⇒ (dy/dx)∣_((x_1 , y_1 )) = 2ax_1 eq. of tangent to parabola at (x_1 , ax_1 ^2 ) is y−ax_1 ^2 =2ax_1 (x−x_1 ) slope of common tangent to circles at T : m= cot θ T (Rcos θ, R−Rsin θ) let 2ax_1 = cot θ y_1 =ax_1 ^2 y_1 =ax_1 ^2 and cot θ = 2ax_1 x_1 = (R−2r)cos θ y_1 =R−(R−2r)sin θ ⇒ R−(R−2r)sin θ = ax_1 ^2 R−(√((R−2r)^2 −x_1 ^2 )) = ax_1 ^2 ⇒ (R−2r)^2 −x_1 ^2 =a^2 x_1 ^4 +R^2 −2aRx_1 ^2 only one value of x_1 ⇒ (1−2aR)^2 = 4a^2 (4rR−4r^2 ) ⇒ r^2 −rR+(((1−2aR)^2 )/(16a^2 )) =0 r= (R/2)−(√((R^2 /4)−(((1−4aR+4a^2 R^2 ))/(16a^2 )))) ⇒ r=(R/2)−(√((R/(4a))−(1/(16a^2 )))) ⇒ r = (R/2)−((√(4aR−1))/(4a)) .
$${Eq}.\:{of}\:{parabola} \\ $$$$\:\:\:\:\:\:{y}=\:{ax}^{\mathrm{2}} \:\:\:\:\:\Rightarrow\:\:\frac{{dy}}{{dx}}\mid_{\left({x}_{\mathrm{1}} ,\:{y}_{\mathrm{1}} \right)} \:=\:\mathrm{2}{ax}_{\mathrm{1}} \\ $$$${eq}.\:{of}\:{tangent}\:{to}\:{parabola}\:{at} \\ $$$$\left({x}_{\mathrm{1}} ,\:{ax}_{\mathrm{1}} ^{\mathrm{2}} \right)\:{is} \\ $$$$\:\:\:{y}−{ax}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2}{ax}_{\mathrm{1}} \left({x}−{x}_{\mathrm{1}} \right) \\ $$$${slope}\:{of}\:{common}\:{tangent}\:{to} \\ $$$${circles}\:{at}\:{T}\::\:\:{m}=\:\mathrm{cot}\:\theta \\ $$$${T}\:\left({R}\mathrm{cos}\:\theta,\:{R}−{R}\mathrm{sin}\:\theta\right) \\ $$$$\:{let}\:\:\mathrm{2}{ax}_{\mathrm{1}} \:=\:\mathrm{cot}\:\theta\: \\ $$$$\:\:\:{y}_{\mathrm{1}} ={ax}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${y}_{\mathrm{1}} ={ax}_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\:\:\:{and}\:\:\mathrm{cot}\:\theta\:=\:\mathrm{2}{ax}_{\mathrm{1}} \\ $$$${x}_{\mathrm{1}} =\:\left({R}−\mathrm{2}{r}\right)\mathrm{cos}\:\theta \\ $$$${y}_{\mathrm{1}} ={R}−\left({R}−\mathrm{2}{r}\right)\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:{R}−\left({R}−\mathrm{2}{r}\right)\mathrm{sin}\:\theta\:=\:{ax}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${R}−\sqrt{\left({R}−\mathrm{2}{r}\right)^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} }\:=\:{ax}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow\:\left({R}−\mathrm{2}{r}\right)^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} ={a}^{\mathrm{2}} {x}_{\mathrm{1}} ^{\mathrm{4}} +{R}^{\mathrm{2}} −\mathrm{2}{aRx}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${only}\:{one}\:{value}\:{of}\:{x}_{\mathrm{1}} \:\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{2}{aR}\right)^{\mathrm{2}} =\:\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{4}{rR}−\mathrm{4}{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} −{rR}+\frac{\left(\mathrm{1}−\mathrm{2}{aR}\right)^{\mathrm{2}} }{\mathrm{16}{a}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$${r}=\:\frac{{R}}{\mathrm{2}}−\sqrt{\frac{{R}^{\mathrm{2}} }{\mathrm{4}}−\frac{\left(\mathrm{1}−\mathrm{4}{aR}+\mathrm{4}{a}^{\mathrm{2}} {R}^{\mathrm{2}} \right)}{\mathrm{16}{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\:{r}=\frac{{R}}{\mathrm{2}}−\sqrt{\frac{{R}}{\mathrm{4}{a}}−\frac{\mathrm{1}}{\mathrm{16}{a}^{\mathrm{2}} }}\: \\ $$$$\Rightarrow\:\:\:\boldsymbol{{r}}\:=\:\frac{\boldsymbol{{R}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{4}{aR}−\mathrm{1}}}{\mathrm{4}{a}}\:. \\ $$
Commented by ajfour last updated on 29/Aug/18
one or two other routes still yield different answers..! please discuss and help..
$${one}\:{or}\:{two}\:{other}\:{routes}\:{still} \\ $$$${yield}\:{different}\:{answers}..! \\ $$$${please}\:{discuss}\:{and}\:{help}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *