Question-42543

Question Number 42543 by solihin last updated on 27/Aug/18

Commented by solihin last updated on 27/Aug/18

q u e s t i o n 1 p l e a s e

Commented by maxmathsup by imad last updated on 27/Aug/18

1) w h e r e t h i s e q u a t i o n i s d e f i n e d ? w e m u s t h a v e 2 x + 1 ⩾ 0 a n d

12 x^{2} + 12 x + 7 = \to Δ^{^{'}} = 6^{2} - 12 \times 7 < 0 \Rightarrow \forall x 12 x^{2} + 12 x + 7 > 0 s o w e m u s t

h a v e x ⩾ - \frac{1}{2}

(e) \Rightarrow 12 x^{2} + 12 x + 7 = {(2 x + 1)}^{4} = {(4 x^{2} + 4 x + 1)}^{2} \Rightarrow

12 x^{2} + 12 x + 7 = {(4 x^{2} + 4 x)}^{2} + 2 (4 x^{2} + 4 x) + 1 \Rightarrow

12 x^{2} + 12 x + 7 = 16 (x^{4} + 2 x^{3} + x^{2}) + 8 x^{2} + 8 x + 1 \Rightarrow

16 x^{4} + 32 x^{3} + 24 x^{2} + 8 x + 1 - 12 x^{2} - 12 x - 7 \Rightarrow

16 x^{4} + 32 x^{3} + 12 x^{2} - 4 x - 6 = 0 \Rightarrow 8 x^{4} + 16 x^{3} + 6 x^{2} - 2 x - 3 = 0

t h e r o o t s o f t h i s e q u a t i o n a r e

x_{1} \sim - 1, 5 (r e a l)

x_{2} \sim - 0, 5 + 0, 5 i (c o m p l e x)

x_{3} \sim - 0, 5 - 0, 5 i (c o m p l e x)

x_{4} \sim 0, 5 (r e a l) x_{1} i s n o t s o l u t i o n b e c a u s e x_{1} < - \frac{1}{2} s o t h e u n i q u e s l u t i o n

i s x_{4} \sim \frac{1}{2} .

Commented by maxmathsup by imad last updated on 27/Aug/18

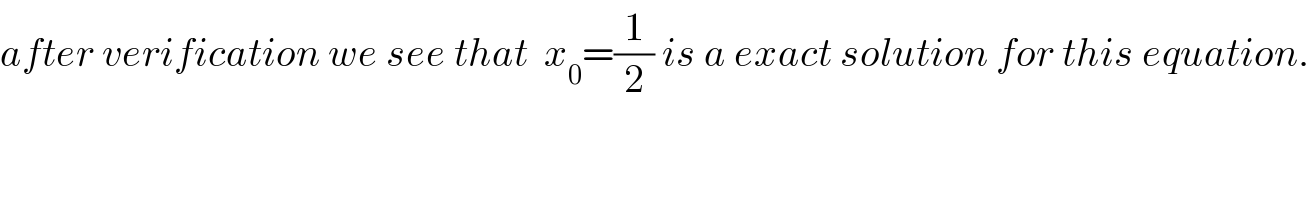
a f t e r v e r i f i c a t i o n w e s e e t h a t x_{0} = \frac{1}{2} i s a e x a c t s o l u t i o n f o r t h i s e q u a t i o n .