Question-42559

Question Number 42559 by Tawa1 last updated on 27/Aug/18

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

15)a+(1/a)=((√a) −(1/( (√a))))^2 +2 so a+(1/a)=2 if ((√a) −(1/( (√a) )))=0 a+(1/a)>2 if((√a) −(1/( (√a))))>0

$$\left.\mathrm{15}\right){a}+\frac{\mathrm{1}}{{a}}=\left(\sqrt{{a}}\:−\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)^{\mathrm{2}} +\mathrm{2}\: \\ $$$${so}\:{a}+\frac{\mathrm{1}}{{a}}=\mathrm{2}\:{if}\:\left(\sqrt{{a}}\:−\frac{\mathrm{1}}{\:\sqrt{{a}}\:}\right)=\mathrm{0} \\ $$$${a}+\frac{\mathrm{1}}{{a}}>\mathrm{2}\:{if}\left(\sqrt{{a}}\:−\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)>\mathrm{0} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 27/Aug/18

So, that is all, God bless you sir. i really appreciate

$$\mathrm{So},\:\mathrm{that}\:\mathrm{is}\:\mathrm{all},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

AM≥GM (a+b)((1/a)+(1/b)) ((a+b)/2)≥(√(ab)) (((1/a)+(1/b))/2)≥(√((1/a)×(1/b))) multiply ((a+b)/2)×(((1/a)+(1/b))/2)≥1 (a+b)((1/a)+(1/b))≥4

$${AM}\geqslant{GM} \\ $$$$\left({a}+{b}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right) \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}}\: \\ $$$$\frac{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}}{\mathrm{2}}\geqslant\sqrt{\frac{\mathrm{1}}{{a}}×\frac{\mathrm{1}}{{b}}}\: \\ $$$${multiply} \\ $$$$\frac{{a}+{b}}{\mathrm{2}}×\frac{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}}{\mathrm{2}}\geqslant\mathrm{1}\:\:\:\:\left({a}+{b}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\geqslant\mathrm{4} \\ $$

Commented by Tawa1 last updated on 27/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

((a+b)/2)×((b+c)/2)×((c+a)/2)≥(√(ab)) ×(√(bc)) ×(√(ac)) (a+b)(b+c)(c+a)≥8abc

$$\frac{{a}+{b}}{\mathrm{2}}×\frac{{b}+{c}}{\mathrm{2}}×\frac{{c}+{a}}{\mathrm{2}}\geqslant\sqrt{{ab}}\:×\sqrt{{bc}}\:×\sqrt{{ac}}\: \\ $$$$\left({a}+{b}\right)\left({b}+{c}\right)\left({c}+{a}\right)\geqslant\mathrm{8}{abc} \\ $$

Commented by malwaan last updated on 29/Aug/18

$$\mathrm{good}\:\mathrm{work} \\ $$$$\mathrm{thanks}\:\mathrm{alot} \\ $$

Commented by Tawa1 last updated on 27/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

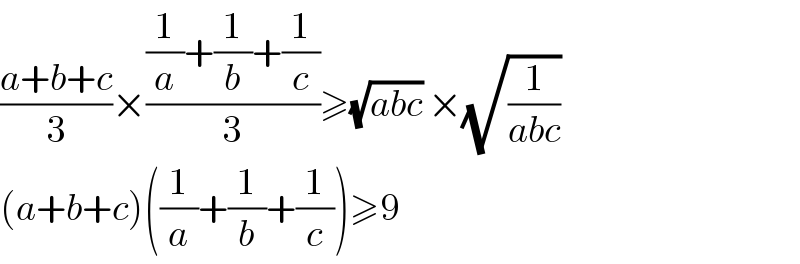
((a+b+c)/3)×(((1/a)+(1/b)+(1/c))/3)≥(√(abc)) ×(√(1/(abc))) (a+b+c)((1/a)+(1/b)+(1/c))≥9

$$\frac{{a}+{b}+{c}}{\mathrm{3}}×\frac{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}}{\mathrm{3}}\geqslant\sqrt{{abc}}\:×\sqrt{\frac{\mathrm{1}}{{abc}}}\: \\ $$$$\left({a}+{b}+{c}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\geqslant\mathrm{9} \\ $$

Commented by Tawa1 last updated on 27/Aug/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

((a+b)/2)≥(√(ab)) (1/2)≥(√(ab)) 1≥2(√(ab)) 1≥4ab a^2 +b^2 =(a+b)^2 −2ab =1−2×(1/4) =(1/2) (

$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\geqslant\sqrt{{ab}} \\ $$$$\mathrm{1}\geqslant\mathrm{2}\sqrt{{ab}} \\ $$$$\mathrm{1}\geqslant\mathrm{4}{ab} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$=\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}{ab} \\ $$$$=\mathrm{1}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\left(\right. \\ $$

Commented by Tawa1 last updated on 27/Aug/18

God bless you sir. I appreciate your time and effort

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{and}\:\mathrm{effort} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply