Question Number 42592 by Aston last updated on 28/Aug/18
Answered by $@ty@m last updated on 28/Aug/18

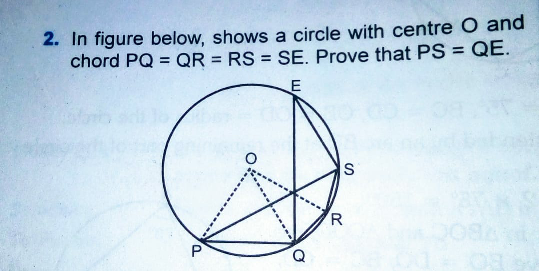
$${Let}\:{PS}\:{and}\:{QE}\:{intersects}\:{at}\:{M}. \\ $$$${In}\:\bigtriangleup{PMQ}\:{and}\:\bigtriangleup{EMS}, \\ $$$$\angle{QPM}=\angle{SEM}\:\left({angle}\:{of}\:{the}\:{same}\:{segment}\right) \\ $$$${PQ}={ES}\:\left({given}\right) \\ $$$$\angle{PQM}=\angle{ESM}\:\left({angle}\:{of}\:{the}\:{same}\:{segment}\right) \\ $$$$\therefore\bigtriangleup{PMQ}\:\cong\:\bigtriangleup{EMS},\:{by}\:{ASA}\:{axiom} \\ $$$$\therefore{PM}={EM}\:….\left(\mathrm{1}\right) \\ $$$$\&\:{QM}={MS}\:….\left(\mathrm{2}\right) \\ $$$${Adding}\:\left(\mathrm{1}\right)\:\&\:\left(\mathrm{2}\right) \\ $$$${PM}+{MS}={EM}\:+{QM} \\ $$$${PS}={EQ} \\ $$$${Q}.{E}.{D}. \\ $$
Commented by $@ty@m last updated on 29/Aug/18

Commented by Vashu last updated on 29/Aug/18

$${EXPLAIN}\:{ANGLE}\:{OF}\:{SAME}\:{SEGMENT} \\ $$$${WHAT}\:{IS}\:{THIS}\:?\: \\ $$
Commented by $@ty@m last updated on 29/Aug/18

