Question Number 42593 by aseerimad last updated on 28/Aug/18
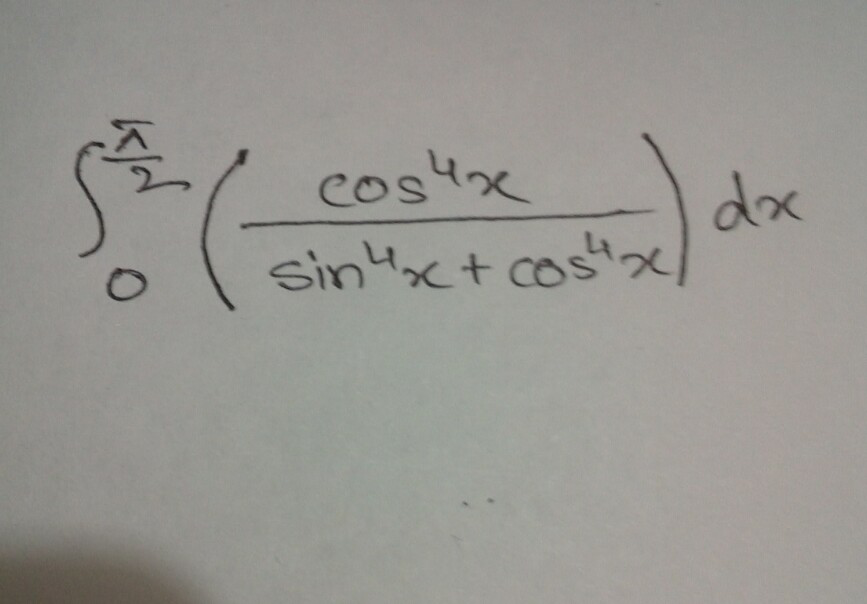
Commented by maxmathsup by imad last updated on 28/Aug/18
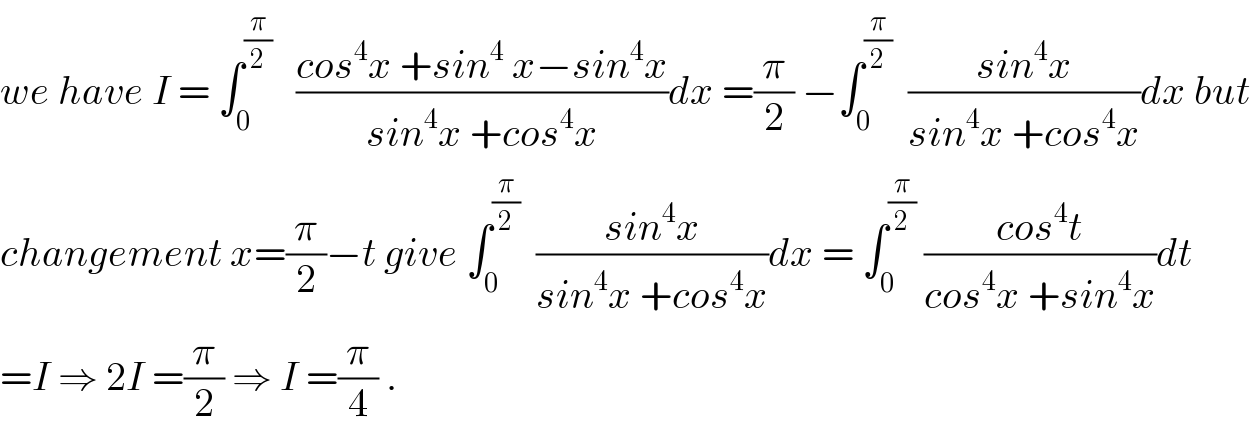
$${we}\:{have}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} \:{x}−{sin}^{\mathrm{4}} {x}}{{sin}^{\mathrm{4}} {x}\:+{cos}^{\mathrm{4}} {x}}{dx}\:=\frac{\pi}{\mathrm{2}}\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}^{\mathrm{4}} {x}}{{sin}^{\mathrm{4}} {x}\:+{cos}^{\mathrm{4}} {x}}{dx}\:{but} \\ $$$${changement}\:{x}=\frac{\pi}{\mathrm{2}}−{t}\:{give}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}^{\mathrm{4}} {x}}{{sin}^{\mathrm{4}} {x}\:+{cos}^{\mathrm{4}} {x}}{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cos}^{\mathrm{4}} {t}}{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}}{dt} \\ $$$$={I}\:\Rightarrow\:\mathrm{2}{I}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{4}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Aug/18
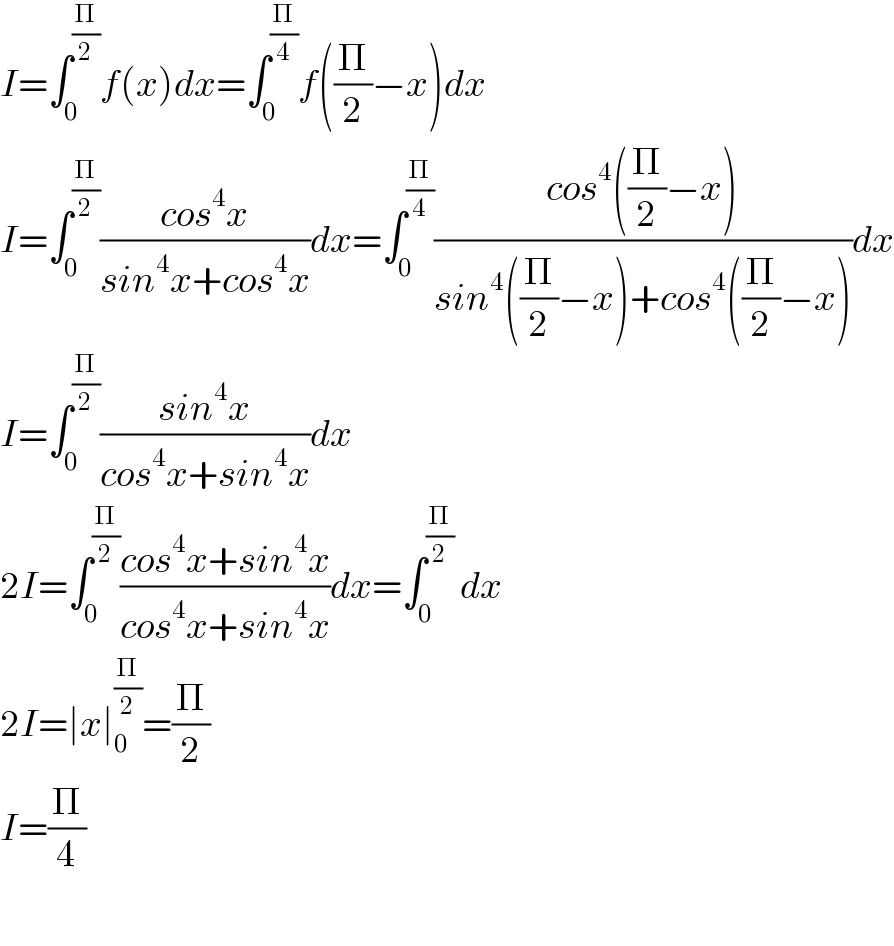
$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {f}\left(\frac{\Pi}{\mathrm{2}}−{x}\right){dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{4}} {x}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}}{dx}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{cos}^{\mathrm{4}} \left(\frac{\Pi}{\mathrm{2}}−{x}\right)}{{sin}^{\mathrm{4}} \left(\frac{\Pi}{\mathrm{2}}−{x}\right)+{cos}^{\mathrm{4}} \left(\frac{\Pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{4}} {x}}{{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}}{{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}}{dx}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:{dx} \\ $$$$\mathrm{2}{I}=\mid{x}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} =\frac{\Pi}{\mathrm{2}} \\ $$$${I}=\frac{\Pi}{\mathrm{4}} \\ $$$$ \\ $$
