Menu Close

Question-42897

Tinku Tara 0 Comments
Pin




Question Number 42897 by Joel578 last updated on 04/Sep/18
Commented by Joel578 last updated on 04/Sep/18
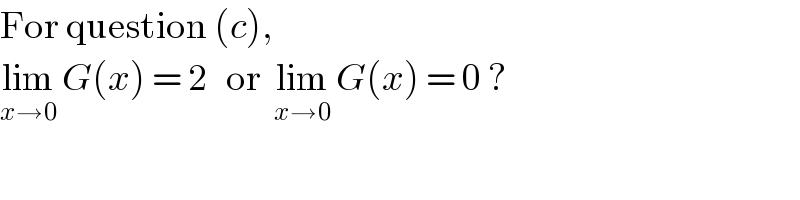
For question (c), lim_(x→0) G(x) = 2 or lim_(x→0) G(x) = 0 ?
$$\mathrm{For}\:\mathrm{question}\:\left({c}\right), \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{G}\left({x}\right)\:=\:\mathrm{2}\:\:\:\mathrm{or}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{G}\left({x}\right)\:=\:\mathrm{0}\:? \\ $$
Answered by MJS last updated on 04/Sep/18
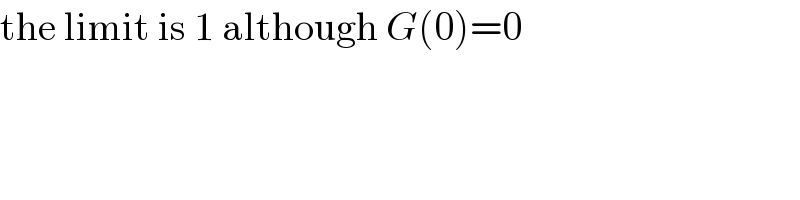
the limit is 1 although G(0)=0
$$\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{1}\:\mathrm{although}\:{G}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
a)lim_(x→0−) G(x)=1 b)lim_(x→0+) G(x)=1 now lim_(x→0−) G(x) is called left hand side limit lim_(x→0+) G(x) is called right hand side limit limit exist if lim_(x→0−) G(x) =lim_(x→0+) G(x) that is lim_(x→0) G(x)=lim_(x→0−) G(x) =lim_(x→0+) G(x) here lim_(x→0−) G(x)=1=lim_(x→0+) G(x) so the value of lim_(x→0 ) G(x)=1 so c) lim_(x→0) G(x) =1 but the function is discontinue at x= 0 so G(0) can not be found out we can not find the value of G(x) at x=0 d)can not be find the value of G(x) at x=0 that is G(0) not defined the curve G(x) is discontinue at x=0 further we can say G(x) is discontinue at x=0 we can not find ((dG(x))/dx) at x=0 c)lim_(x→0) G(x)=li_(x→0−) li_(x→0)
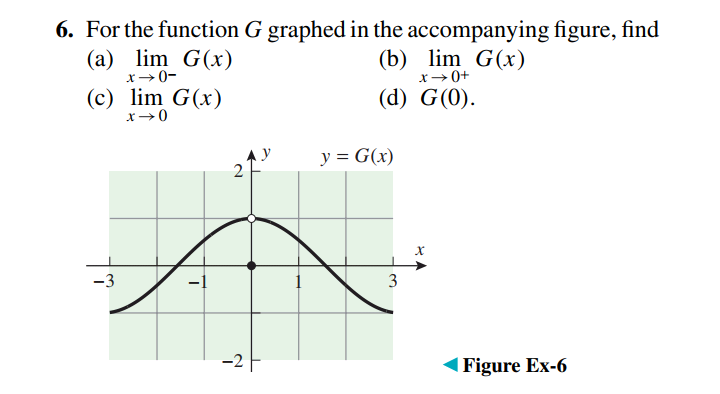
$$\left.{a}\right)\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:{G}\left({x}\right)=\mathrm{1} \\ $$$$\left.{b}\right)\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:{G}\left({x}\right)=\mathrm{1} \\ $$$${now}\:\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:{G}\left({x}\right)\:{is}\:{called}\:{left}\:{hand}\:{side}\:{limit} \\ $$$$\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:{G}\left({x}\right)\:{is}\:{called}\:{right}\:{hand}\:{side}\:{limit} \\ $$$${limit}\:{exist}\:{if}\:\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:{G}\left({x}\right)\:\:=\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:{G}\left({x}\right) \\ $$$${that}\:{is}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{G}\left({x}\right)=\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:{G}\left({x}\right)\:=\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:{G}\left({x}\right) \\ $$$${here}\:\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:{G}\left({x}\right)=\mathrm{1}=\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:{G}\left({x}\right) \\ $$$${so}\:{the}\:{value}\:{of}\:\underset{{x}\rightarrow\mathrm{0}\:\:} {\mathrm{lim}}\:{G}\left({x}\right)=\mathrm{1} \\ $$$$\left.{so}\:{c}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{G}\left({x}\right)\:=\mathrm{1} \\ $$$${but}\:{the}\:{function}\:{is}\:{discontinue}\:{at}\:{x}=\:\mathrm{0} \\ $$$${so}\:{G}\left(\mathrm{0}\right)\:{can}\:{not}\:{be}\:{found}\:{out} \\ $$$${we}\:{can}\:{not}\:{find}\:{the}\:{value}\:{of}\:{G}\left({x}\right)\:{at}\:{x}=\mathrm{0} \\ $$$$\left.{d}\right){can}\:{not}\:{be}\:{find}\:{the}\:{value}\:{of}\:{G}\left({x}\right)\:{at}\:{x}=\mathrm{0} \\ $$$${that}\:{is}\:{G}\left(\mathrm{0}\right)\:{not}\:{defined} \\ $$$${the}\:{curve}\:{G}\left({x}\right)\:{is}\:{discontinue}\:{at}\:{x}=\mathrm{0} \\ $$$${further}\:{we}\:{can}\:{say}\:{G}\left({x}\right)\:{is}\:{discontinue}\:{at}\:{x}=\mathrm{0} \\ $$$${we}\:{can}\:{not}\:{find}\:\frac{{dG}\left({x}\right)}{{dx}}\:{at}\:{x}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\left.{c}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{G}\left({x}\right)=\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{li}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$
Commented by Joel578 last updated on 04/Sep/18
Okay, thank you for clearing my doubt
$$\mathrm{Okay},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{clearing}\:\mathrm{my}\:\mathrm{doubt} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *