Menu Close

Question-42948

Tinku Tara 0 Comments
Pin




Question Number 42948 by ajfour last updated on 05/Sep/18
Commented by ajfour last updated on 05/Sep/18
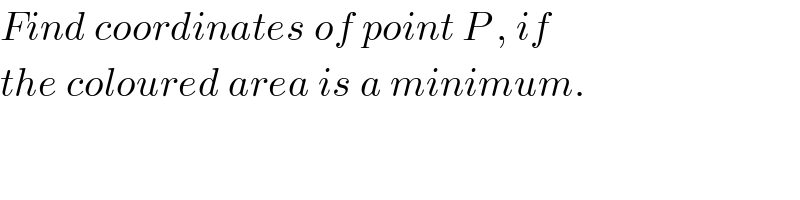
Find coordinates of point P , if the coloured area is a minimum.
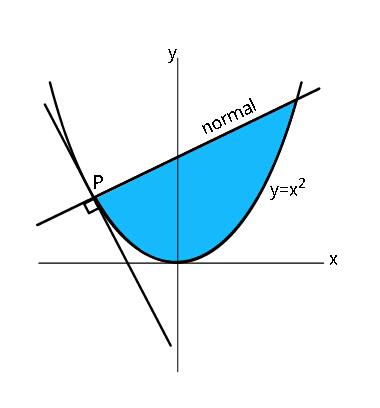
$${Find}\:{coordinates}\:{of}\:{point}\:{P}\:,\:{if} \\ $$$${the}\:{coloured}\:{area}\:{is}\:{a}\:{minimum}. \\ $$
Commented by MJS last updated on 05/Sep/18
this is not very hard, I′ll post the answer later if noone else will have done it... but now find (1) the greatest triangle (2) the greatest circle (3) the greatest trapezoid fitting into the found blue area
$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{very}\:\mathrm{hard},\:\mathrm{I}'\mathrm{ll}\:\mathrm{post}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{later} \\ $$$$\mathrm{if}\:\mathrm{noone}\:\mathrm{else}\:\mathrm{will}\:\mathrm{have}\:\mathrm{done}\:\mathrm{it}… \\ $$$$\mathrm{but}\:\mathrm{now}\:\mathrm{find} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{triangle} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{circle} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{trapezoid} \\ $$$$\mathrm{fitting}\:\mathrm{into}\:\mathrm{the}\:\mathrm{found}\:\mathrm{blue}\:\mathrm{area} \\ $$
Commented by malwaan last updated on 06/Sep/18
please solve it
$$\mathrm{please}\:\mathrm{solve}\:\mathrm{it} \\ $$
Commented by ajfour last updated on 06/Sep/18
Commented by ajfour last updated on 06/Sep/18
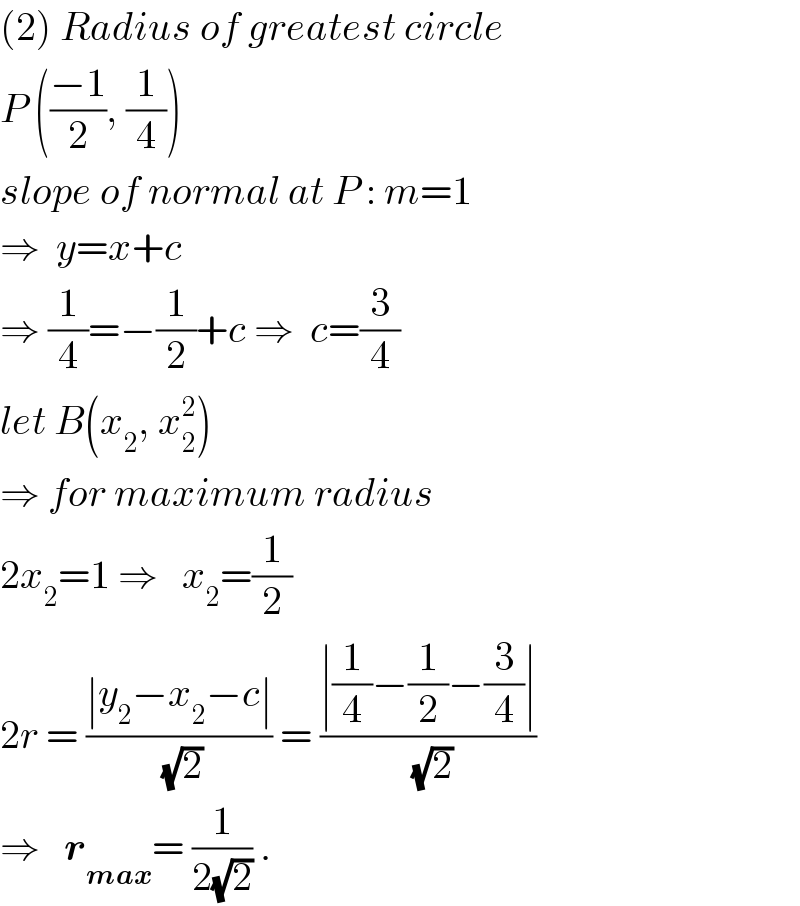
(2) Radius of greatest circle P (((−1)/2), (1/4)) slope of normal at P : m=1 ⇒ y=x+c ⇒ (1/4)=−(1/2)+c ⇒ c=(3/4) let B(x_2 , x_2 ^2 ) ⇒ for maximum radius 2x_2 =1 ⇒ x_2 =(1/2) 2r = ((∣y_2 −x_2 −c∣)/( (√2))) = ((∣(1/4)−(1/2)−(3/4)∣)/( (√2))) ⇒ r_(max) = (1/(2(√2))) .
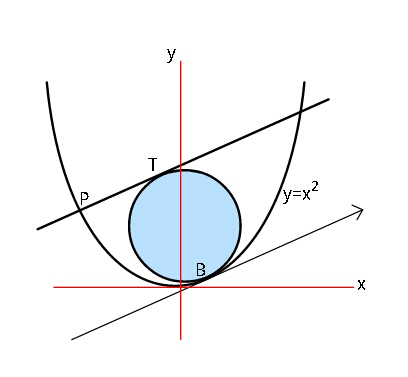
$$\left(\mathrm{2}\right)\:{Radius}\:{of}\:{greatest}\:{circle} \\ $$$${P}\:\left(\frac{−\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$${slope}\:{of}\:{normal}\:{at}\:{P}\::\:{m}=\mathrm{1} \\ $$$$\Rightarrow\:\:{y}={x}+{c} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}}+{c}\:\Rightarrow\:\:{c}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${let}\:{B}\left({x}_{\mathrm{2}} ,\:{x}_{\mathrm{2}} ^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{for}\:{maximum}\:{radius} \\ $$$$\mathrm{2}{x}_{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:\:\:{x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{r}\:=\:\frac{\mid{y}_{\mathrm{2}} −{x}_{\mathrm{2}} −{c}\mid}{\:\sqrt{\mathrm{2}}}\:=\:\frac{\mid\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\mid}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{r}}_{\boldsymbol{{max}}} =\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$
Answered by ajfour last updated on 05/Sep/18
let eq. of normal be y=mx+c for points of intersection x^2 = mx+c ⇒ x_1 +x_2 =m and x_1 x_2 =−c further 2mx_1 =−1 ⇒ m=−(1/(2x_1 )) , x_2 = −(1/(2x_1 ))−x_1 c=(1/2)+x_1 ^2 ⇒ (dx_2 /dx_1 )=(1/(2x_1 ^2 ))−1 Area A= ∫_x_1 ^( x_2 ) (mx+c−x^2 )dx (dA/dx_1 )=0 ⇒ ∫_x_1 ^x_2 (x(dm/dx_1 )+(dc/dx_1 ))dx + (dx_2 /dx_1 )(mx_2 +c−x_2 ^2 )−(mx_1 +c−x_1 ^2 )=0 ⇒ ∫_x_1 ^x_2 ((x/(2x_1 ^2 ))+2x_1 )dx +((1/(2x_1 ^2 ))−1)((1/(4x_1 ^2 ))+(1/2)+(1/2)+x_1 ^2 −(1/(4x_1 ^2 ))−x_1 ^2 −1) −( −(1/2)+(1/2)+x_1 ^2 −x_1 ^2 )=0 ⇒ ∫_x_1 ^x_2 ((x/(2x_1 ^2 ))+2x_1 )dx =0 ⇒ (((x_2 ^2 −x_1 ^2 ))/(4x_1 ^2 ))+2x_1 (x_2 −x_1 )=0 ⇒ ((x_2 +x_1 )/(4x_1 ^2 )) = −2x_1 or −(1/(2x_1 )) = −8x_1 ^3 ⇒ x_1 ^2 = (1/4) ⇒ P (±(1/2), (1/4)) .
$${let}\:{eq}.\:{of}\:{normal}\:{be} \\ $$$${y}={mx}+{c} \\ $$$${for}\:{points}\:{of}\:{intersection} \\ $$$${x}^{\mathrm{2}} =\:{mx}+{c} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} ={m}\:\: \\ $$$${and}\:\:\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} =−{c} \\ $$$${further}\:\:\:\mathrm{2}{mx}_{\mathrm{1}} =−\mathrm{1} \\ $$$$\Rightarrow\:{m}=−\frac{\mathrm{1}}{\mathrm{2}{x}_{\mathrm{1}} }\:,\:{x}_{\mathrm{2}} =\:−\frac{\mathrm{1}}{\mathrm{2}{x}_{\mathrm{1}} }−{x}_{\mathrm{1}} \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{2}}+{x}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{dx}_{\mathrm{2}} }{{dx}_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} }−\mathrm{1} \\ $$$${Area}\:{A}=\:\int_{{x}_{\mathrm{1}} } ^{\:{x}_{\mathrm{2}} } \left({mx}+{c}−{x}^{\mathrm{2}} \right){dx} \\ $$$$\frac{{dA}}{{dx}_{\mathrm{1}} }=\mathrm{0}\:\Rightarrow\:\:\:\:\int_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } \left({x}\frac{{dm}}{{dx}_{\mathrm{1}} }+\frac{{dc}}{{dx}_{\mathrm{1}} }\right){dx}\:+ \\ $$$$\frac{{dx}_{\mathrm{2}} }{{dx}_{\mathrm{1}} }\left({mx}_{\mathrm{2}} +{c}−{x}_{\mathrm{2}} ^{\mathrm{2}} \right)−\left({mx}_{\mathrm{1}} +{c}−{x}_{\mathrm{1}} ^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\int_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } \left(\frac{{x}}{\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} }+\mathrm{2}{x}_{\mathrm{1}} \right){dx} \\ $$$$\:\:\:\:\:+\left(\frac{\mathrm{1}}{\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} }−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{x}_{\mathrm{1}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} }−{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\left(\:−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{x}_{\mathrm{1}} ^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\int_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } \left(\frac{{x}}{\mathrm{2}{x}_{\mathrm{1}} ^{\mathrm{2}} }+\mathrm{2}{x}_{\mathrm{1}} \right){dx}\:=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\left({x}_{\mathrm{2}} ^{\mathrm{2}} −{x}_{\mathrm{1}} ^{\mathrm{2}} \right)}{\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} }+\mathrm{2}{x}_{\mathrm{1}} \left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\frac{{x}_{\mathrm{2}} +{x}_{\mathrm{1}} }{\mathrm{4}{x}_{\mathrm{1}} ^{\mathrm{2}} }\:=\:−\mathrm{2}{x}_{\mathrm{1}} \\ $$$${or}\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}{x}_{\mathrm{1}} }\:=\:−\mathrm{8}{x}_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:{x}_{\mathrm{1}} ^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\Rightarrow\:\boldsymbol{{P}}\:\left(\pm\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{4}}\right)\:. \\ $$$$ \\ $$
Commented by ajfour last updated on 05/Sep/18
Have i solved it correct, Sir ?
$${Have}\:{i}\:{solved}\:{it}\:{correct},\:{Sir}\:? \\ $$
Commented by MJS last updated on 05/Sep/18
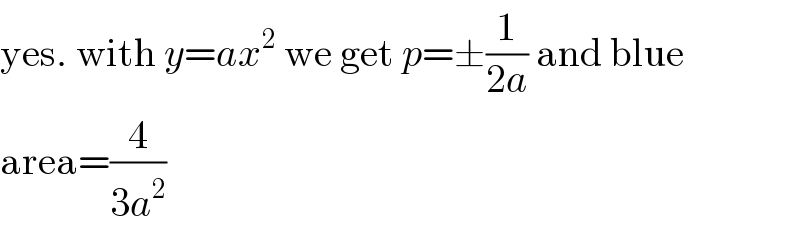
yes. with y=ax^2 we get p=±(1/(2a)) and blue area=(4/(3a^2 ))
$$\mathrm{yes}.\:\mathrm{with}\:{y}={ax}^{\mathrm{2}} \:\mathrm{we}\:\mathrm{get}\:{p}=\pm\frac{\mathrm{1}}{\mathrm{2}{a}}\:\mathrm{and}\:\mathrm{blue} \\ $$$$\mathrm{area}=\frac{\mathrm{4}}{\mathrm{3}{a}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 05/Sep/18
Thanks Sir.
$${Thanks}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *