Menu Close

Question-43125

Tinku Tara 0 Comments
Pin




Question Number 43125 by Raj Singh last updated on 07/Sep/18
Commented by maxmathsup by imad last updated on 07/Sep/18
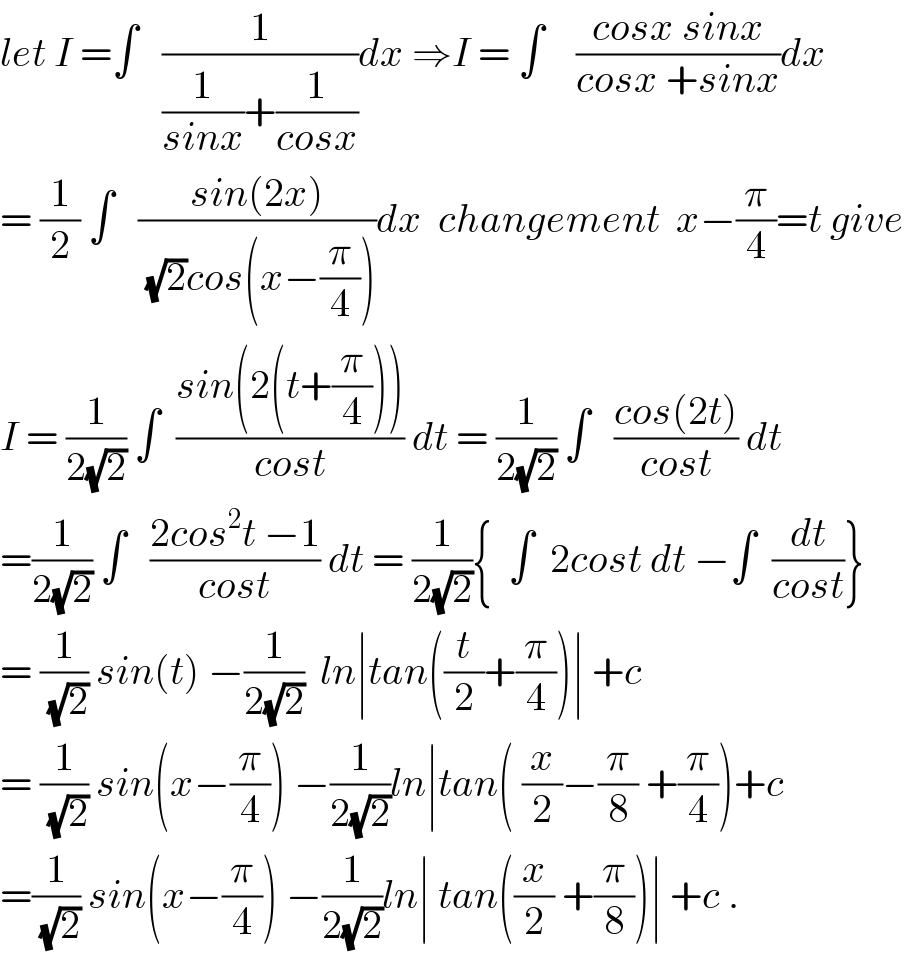
let I =∫ (1/((1/(sinx))+(1/(cosx))))dx ⇒I = ∫ ((cosx sinx)/(cosx +sinx))dx = (1/2) ∫ ((sin(2x))/( (√2)cos(x−(π/4))))dx changement x−(π/4)=t give I = (1/(2(√2))) ∫ ((sin(2(t+(π/4))))/(cost)) dt = (1/(2(√2))) ∫ ((cos(2t))/(cost)) dt =(1/(2(√2))) ∫ ((2cos^2 t −1)/(cost)) dt = (1/(2(√2))){ ∫ 2cost dt −∫ (dt/(cost))} = (1/( (√2))) sin(t) −(1/(2(√2))) ln∣tan((t/2)+(π/4))∣ +c = (1/( (√2))) sin(x−(π/4)) −(1/(2(√2)))ln∣tan( (x/2)−(π/8) +(π/4))+c =(1/( (√2))) sin(x−(π/4)) −(1/(2(√2)))ln∣ tan((x/2) +(π/8))∣ +c .
$${let}\:{I}\:=\int\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{sinx}}+\frac{\mathrm{1}}{{cosx}}}{dx}\:\Rightarrow{I}\:=\:\int\:\:\:\:\frac{{cosx}\:{sinx}}{{cosx}\:+{sinx}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{\:\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)}{dx}\:\:{changement}\:\:{x}−\frac{\pi}{\mathrm{4}}={t}\:{give}\: \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\:\frac{{sin}\left(\mathrm{2}\left({t}+\frac{\pi}{\mathrm{4}}\right)\right)}{{cost}}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{{cos}\left(\mathrm{2}{t}\right)}{{cost}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{\mathrm{2}{cos}^{\mathrm{2}} {t}\:−\mathrm{1}}{{cost}}\:{dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\:\int\:\:\mathrm{2}{cost}\:{dt}\:−\int\:\:\frac{{dt}}{{cost}}\right\} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{sin}\left({t}\right)\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:{ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid\:+{c} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid{tan}\left(\:\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\:+\frac{\pi}{\mathrm{4}}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{sin}\left({x}−\frac{\pi}{\mathrm{4}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\:{tan}\left(\frac{{x}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{8}}\right)\mid\:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Sep/18
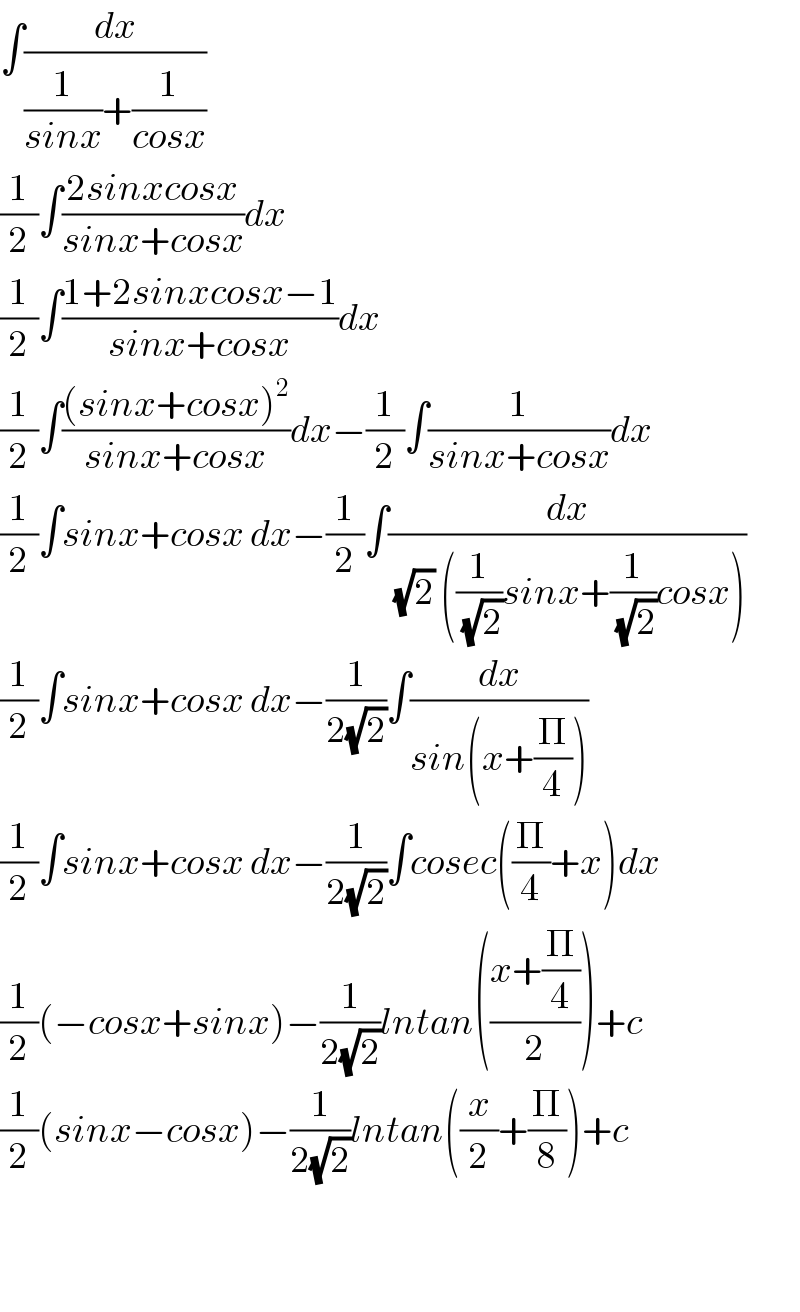
∫(dx/((1/(sinx))+(1/(cosx)))) (1/2)∫((2sinxcosx)/(sinx+cosx))dx (1/2)∫((1+2sinxcosx−1)/(sinx+cosx))dx (1/2)∫(((sinx+cosx)^2 )/(sinx+cosx))dx−(1/2)∫(1/(sinx+cosx))dx (1/2)∫sinx+cosx dx−(1/2)∫(dx/( (√2) ((1/( (√2)))sinx+(1/( (√2)))cosx))) (1/2)∫sinx+cosx dx−(1/(2(√2)))∫(dx/(sin(x+(Π/4)))) (1/2)∫sinx+cosx dx−(1/(2(√2)))∫cosec((Π/4)+x)dx (1/2)(−cosx+sinx)−(1/(2(√2)))lntan(((x+(Π/4))/2))+c (1/2)(sinx−cosx)−(1/(2(√2)))lntan((x/2)+(Π/8))+c
$$\int\frac{{dx}}{\frac{\mathrm{1}}{{sinx}}+\frac{\mathrm{1}}{{cosx}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{sinxcosx}}{{sinx}+{cosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{2}{sinxcosx}−\mathrm{1}}{{sinx}+{cosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({sinx}+{cosx}\right)^{\mathrm{2}} }{{sinx}+{cosx}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{sinx}+{cosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{sinx}+{cosx}\:{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sinx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cosx}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{sinx}+{cosx}\:{dx}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\frac{{dx}}{{sin}\left({x}+\frac{\Pi}{\mathrm{4}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int{sinx}+{cosx}\:{dx}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int{cosec}\left(\frac{\Pi}{\mathrm{4}}+{x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−{cosx}+{sinx}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{lntan}\left(\frac{{x}+\frac{\Pi}{\mathrm{4}}}{\mathrm{2}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({sinx}−{cosx}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{lntan}\left(\frac{{x}}{\mathrm{2}}+\frac{\Pi}{\mathrm{8}}\right)+{c} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *