Question Number 43128 by Cheyboy last updated on 07/Sep/18
Commented by Cheyboy last updated on 07/Sep/18

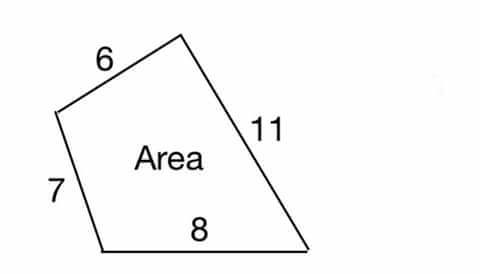
$${Find}\:{the}\:{area} \\ $$
Commented by ajfour last updated on 07/Sep/18
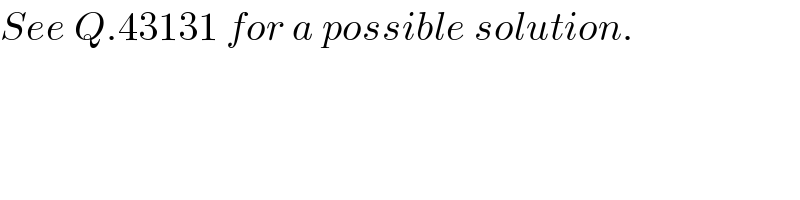
$${See}\:{Q}.\mathrm{43131}\:{for}\:{a}\:{possible}\:{solution}. \\ $$
Commented by Cheyboy last updated on 07/Sep/18
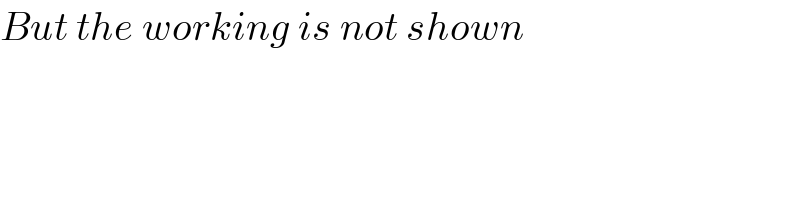
$${But}\:{the}\:{working}\:{is}\:{not}\:{shown} \\ $$
Commented by ajfour last updated on 07/Sep/18
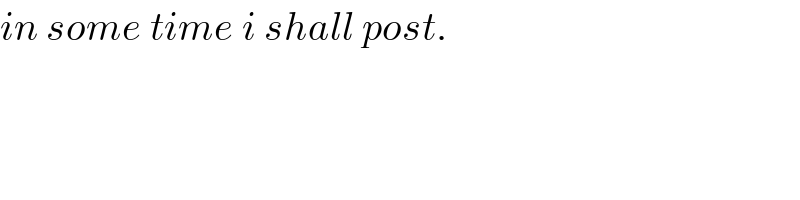
$${in}\:{some}\:{time}\:{i}\:{shall}\:{post}. \\ $$
Commented by Cheyboy last updated on 07/Sep/18

$${Ok}\:{sir}\:{thank}\:{you} \\ $$
Answered by behi83417@gmail.com last updated on 07/Sep/18
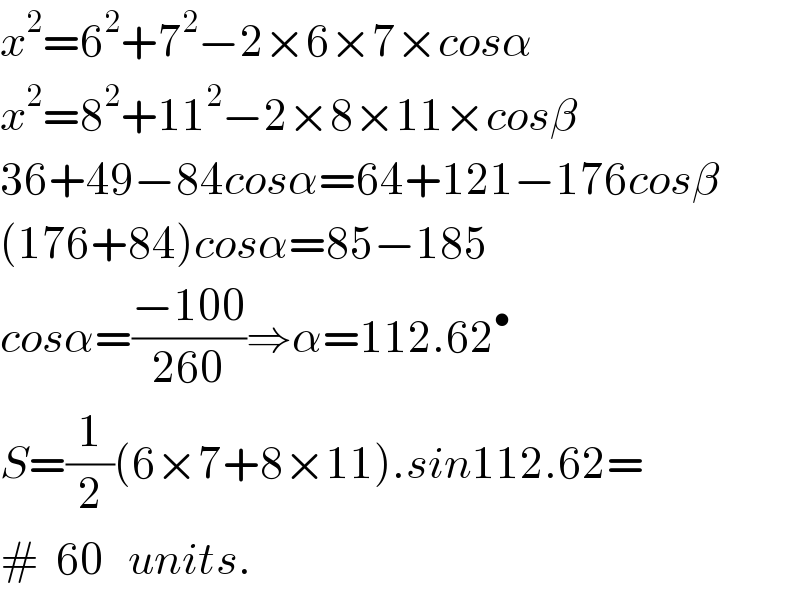
$${x}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{2}×\mathrm{6}×\mathrm{7}×{cos}\alpha \\ $$$${x}^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} +\mathrm{11}^{\mathrm{2}} −\mathrm{2}×\mathrm{8}×\mathrm{11}×{cos}\beta \\ $$$$\mathrm{36}+\mathrm{49}−\mathrm{84}{cos}\alpha=\mathrm{64}+\mathrm{121}−\mathrm{176}{cos}\beta \\ $$$$\left(\mathrm{176}+\mathrm{84}\right){cos}\alpha=\mathrm{85}−\mathrm{185} \\ $$$${cos}\alpha=\frac{−\mathrm{100}}{\mathrm{260}}\Rightarrow\alpha=\mathrm{112}.\mathrm{62}^{\bullet} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{6}×\mathrm{7}+\mathrm{8}×\mathrm{11}\right).{sin}\mathrm{112}.\mathrm{62}= \\ $$$$#\:\:\mathrm{60}\:\:\:{units}. \\ $$
Commented by ajfour last updated on 07/Sep/18
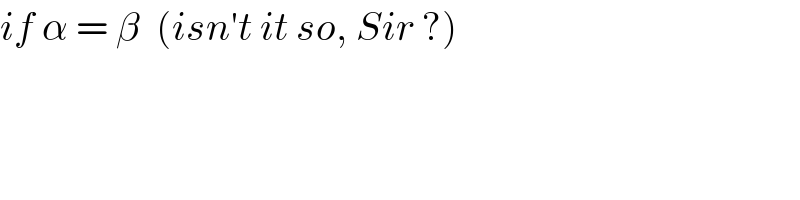
$${if}\:\alpha\:=\:\beta\:\:\left({isn}'{t}\:{it}\:{so},\:{Sir}\:?\right) \\ $$
Commented by behi83417@gmail.com last updated on 07/Sep/18
![no sir.[α+β=π⇒sinα=sinβ]](https://www.tinkutara.com/question/Q43144.png)
$${no}\:{sir}.\left[\alpha+\beta=\pi\Rightarrow{sin}\alpha={sin}\beta\right] \\ $$
Commented by ajfour last updated on 07/Sep/18
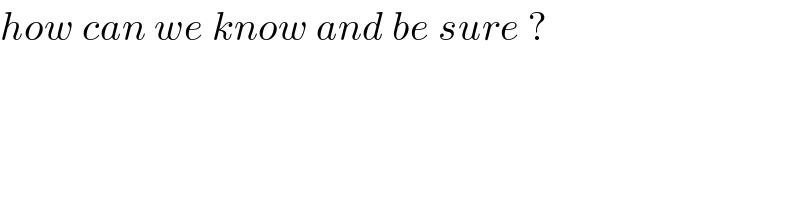
$${how}\:{can}\:{we}\:{know}\:{and}\:{be}\:{sure}\:? \\ $$
Commented by MJS last updated on 07/Sep/18

$$\mathrm{we}\:\mathrm{cannot} \\ $$
