Question Number 43252 by ajfour last updated on 08/Sep/18

Commented by MJS last updated on 08/Sep/18
![circle x^2 +y^2 =1 y=(√(1−x^2 )) parabola x=ay^2 −1 y=(√(a(x+1))); a>0 circle ∩ parabola 1−x^2 =a(x+1) x^2 +ax+(a−1)=0 x_1 =−1 [trivial] x_2 =1−a y_2 =(√(a(2−a))) ((area above parabola)/(area below parabola))=2 ((∫_(−1) ^(1−a) (√(1−x^2 ))dx−∫_(−1) ^(1−a) (√(a(x+1)))dx)/(∫_(−1) ^(1−a) (√(a(x+1)))dx+∫_(1−a) ^1 (√(1−x^2 ))dx))=2 (3/2)(arcsin(1−a)+(1−a)(√(a(2−a))))−2(√(a(2−a)^3 ))−(π/4)=0 a≈.0802770 x_2 ≈.919723 y_2 ≈.392568 α=2arctan (y_2 /x_2 ) ≈46.2288°](https://www.tinkutara.com/question/Q43254.png)
$$\mathrm{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{parabola}\:{x}={ay}^{\mathrm{2}} −\mathrm{1} \\ $$$${y}=\sqrt{{a}\left({x}+\mathrm{1}\right)};\:{a}>\mathrm{0} \\ $$$$\mathrm{circle}\:\cap\:\mathrm{parabola} \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} ={a}\left({x}+\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} +{ax}+\left({a}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1}\:\left[\mathrm{trivial}\right] \\ $$$${x}_{\mathrm{2}} =\mathrm{1}−{a} \\ $$$${y}_{\mathrm{2}} =\sqrt{{a}\left(\mathrm{2}−{a}\right)} \\ $$$$ \\ $$$$\frac{\mathrm{area}\:\mathrm{above}\:\mathrm{parabola}}{\mathrm{area}\:\mathrm{below}\:\mathrm{parabola}}=\mathrm{2} \\ $$$$\frac{\underset{−\mathrm{1}} {\overset{\mathrm{1}−{a}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}−\underset{−\mathrm{1}} {\overset{\mathrm{1}−{a}} {\int}}\sqrt{{a}\left({x}+\mathrm{1}\right)}{dx}}{\underset{−\mathrm{1}} {\overset{\mathrm{1}−{a}} {\int}}\sqrt{{a}\left({x}+\mathrm{1}\right)}{dx}+\underset{\mathrm{1}−{a}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}}=\mathrm{2} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{arcsin}\left(\mathrm{1}−{a}\right)+\left(\mathrm{1}−{a}\right)\sqrt{{a}\left(\mathrm{2}−{a}\right)}\right)−\mathrm{2}\sqrt{{a}\left(\mathrm{2}−{a}\right)^{\mathrm{3}} }−\frac{\pi}{\mathrm{4}}=\mathrm{0} \\ $$$${a}\approx.\mathrm{0802770} \\ $$$${x}_{\mathrm{2}} \approx.\mathrm{919723} \\ $$$${y}_{\mathrm{2}} \approx.\mathrm{392568} \\ $$$$\alpha=\mathrm{2arctan}\:\frac{{y}_{\mathrm{2}} }{{x}_{\mathrm{2}} }\:\approx\mathrm{46}.\mathrm{2288}° \\ $$
Commented by ajfour last updated on 09/Sep/18

$${thank}\:{you}\:{Sir}. \\ $$
Answered by MrW3 last updated on 08/Sep/18
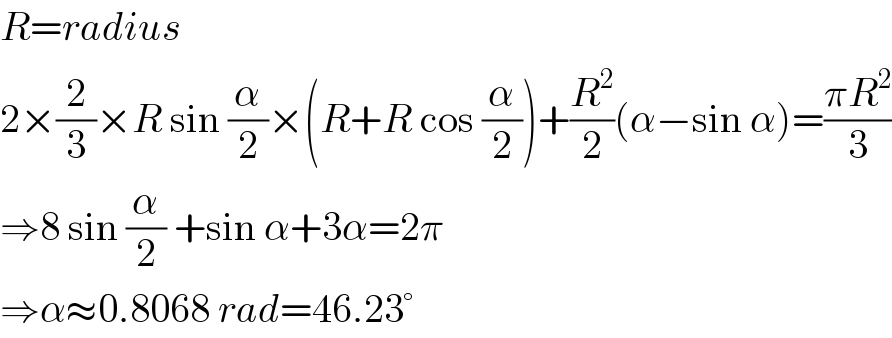
$${R}={radius} \\ $$$$\mathrm{2}×\frac{\mathrm{2}}{\mathrm{3}}×{R}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}×\left({R}+{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)+\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right)=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{8}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:+\mathrm{sin}\:\alpha+\mathrm{3}\alpha=\mathrm{2}\pi \\ $$$$\Rightarrow\alpha\approx\mathrm{0}.\mathrm{8068}\:{rad}=\mathrm{46}.\mathrm{23}° \\ $$
Commented by MrW3 last updated on 09/Sep/18

Commented by MrW3 last updated on 09/Sep/18
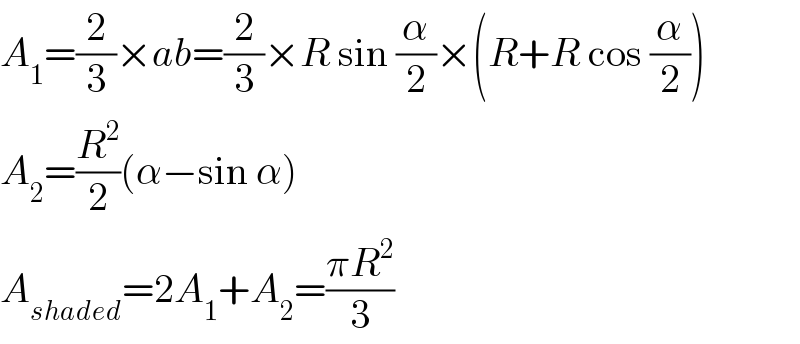
$${A}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}×{ab}=\frac{\mathrm{2}}{\mathrm{3}}×{R}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}×\left({R}+{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$${A}_{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right) \\ $$$${A}_{{shaded}} =\mathrm{2}{A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by ajfour last updated on 09/Sep/18
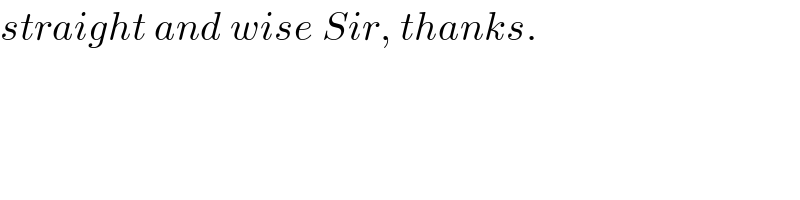
$${straight}\:{and}\:{wise}\:{Sir},\:{thanks}. \\ $$
Commented by MrW3 last updated on 09/Sep/18
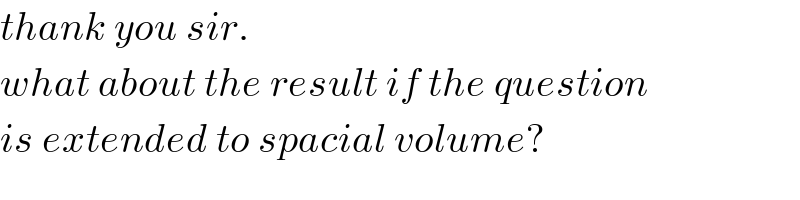
$${thank}\:{you}\:{sir}. \\ $$$${what}\:{about}\:{the}\:{result}\:{if}\:{the}\:{question} \\ $$$${is}\:{extended}\:{to}\:{spacial}\:{volume}? \\ $$
Commented by MrW3 last updated on 09/Sep/18

$${yes}\:{a}\:{sphere}\:{is}\:{divided}\:{into}\:{two}\:{equal} \\ $$$${parts}. \\ $$
Commented by ajfour last updated on 09/Sep/18
$${then}\:{there}\:{are}\:{two}\:{regions},\:{not} \\ $$$${three}! \\ $$
Answered by ajfour last updated on 09/Sep/18
![3D extension: sphere: r^2 +(z−R)^2 =R^2 paraboloid : z = Ar^2 let A(a, Aa^2 ) ⇒ a^2 +(Aa^2 −R)^2 =R^2 ⇒ Aa^2 =R+(√(R^2 −a^2 )) .....(i) or ((Aa^2 )/R)=1+(√(1−((a/R))^2 )) ...(i)^∗ ∫_0 ^( a) (z_(sphere) −z_(para) )(2πrdr)=((2πR^3 )/3) ⇒∫_0 ^( a) [R+(√(R^2 −r^2 ))−Ar^2 ]rdr = (R^3 /3) ....(ii) ((a^2 R)/2)−(((R^2 −a^2 )^(3/2) )/3)+(R^3 /3)−((Aa^4 )/4)=(R^3 /3) (a/R)=x = sin (α/2) ⇒ 6x^2 −4(1−x^2 )^(3/2) = 3x^2 (1+(√(1−x^2 )) ) ⇒ 6sin^2 (α/2)−4cos^3 (α/2)=3(sin^2 (α/2))(1+cos (α/2)) let cos (α/2) = p ⇒ 6(1−p^2 )−4p^3 =3(1−p^2 )(1+p) ⇒ p^3 +3p^2 +3p+1 = 4 ⇒ (p+1)^3 =4 p = (4)^(1/3) −1 𝛂 = 2cos^(−1) p = 2cos^(−1) ((4)^(1/3) −1) ≈ 108.0545 .](https://www.tinkutara.com/question/Q43314.png)
$$\mathrm{3}{D}\:{extension}: \\ $$$${sphere}:\:\:{r}^{\mathrm{2}} +\left({z}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${paraboloid}\::\:\:\:{z}\:=\:{Ar}^{\mathrm{2}} \\ $$$${let}\:{A}\left({a},\:{Aa}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} +\left({Aa}^{\mathrm{2}} −{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{Aa}^{\mathrm{2}} ={R}+\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:\:\:\:…..\left({i}\right) \\ $$$${or}\:\:\:\:\:\frac{{Aa}^{\mathrm{2}} }{{R}}=\mathrm{1}+\sqrt{\mathrm{1}−\left(\frac{{a}}{{R}}\right)^{\mathrm{2}} }\:\:\:…\left({i}\right)^{\ast} \\ $$$$\int_{\mathrm{0}} ^{\:\:{a}} \left({z}_{{sphere}} −{z}_{{para}} \right)\left(\mathrm{2}\pi{rdr}\right)=\frac{\mathrm{2}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\:{a}} \left[{R}+\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }−{Ar}^{\mathrm{2}} \right]{rdr}\:=\:\frac{{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\frac{{a}^{\mathrm{2}} {R}}{\mathrm{2}}−\frac{\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}+\frac{{R}^{\mathrm{3}} }{\mathrm{3}}−\frac{{Aa}^{\mathrm{4}} }{\mathrm{4}}=\frac{{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\:\:\frac{{a}}{{R}}={x}\:=\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} =\:\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right) \\ $$$$\Rightarrow\:\mathrm{6sin}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}−\mathrm{4cos}\:^{\mathrm{3}} \frac{\alpha}{\mathrm{2}}=\mathrm{3}\left(\mathrm{sin}\:^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$${let}\:\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:=\:{p} \\ $$$$\Rightarrow\:\mathrm{6}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)−\mathrm{4}{p}^{\mathrm{3}} =\mathrm{3}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)\left(\mathrm{1}+{p}\right) \\ $$$$\Rightarrow\:{p}^{\mathrm{3}} +\mathrm{3}{p}^{\mathrm{2}} +\mathrm{3}{p}+\mathrm{1}\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\:\left({p}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{4}}−\mathrm{1} \\ $$$$\:\:\:\:\boldsymbol{\alpha}\:=\:\mathrm{2cos}^{−\mathrm{1}} \boldsymbol{{p}}\:=\:\mathrm{2cos}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\mathrm{4}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\approx\:\mathrm{108}.\mathrm{0545}\:. \\ $$
Commented by MrW3 last updated on 09/Sep/18
$${wow},\:{such}\:{a}\:{clean}\:{solution}!\:{thank}\:{you} \\ $$$${so}\:{much}! \\ $$
Answered by MrW3 last updated on 09/Sep/18
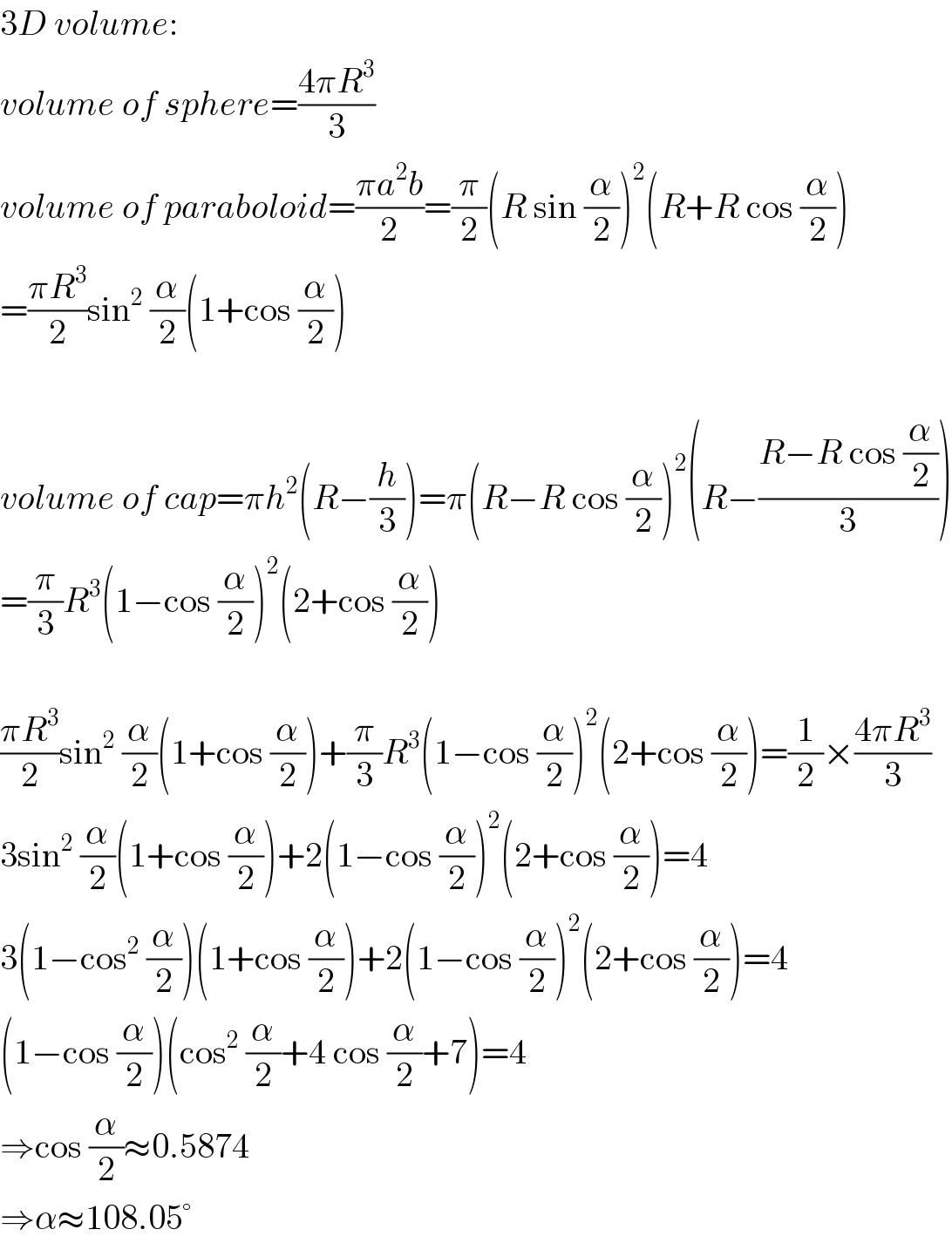
$$\mathrm{3}{D}\:{volume}: \\ $$$${volume}\:{of}\:{sphere}=\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${volume}\:{of}\:{paraboloid}=\frac{\pi{a}^{\mathrm{2}} {b}}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}\left({R}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left({R}+{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\frac{\pi{R}^{\mathrm{3}} }{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$$ \\ $$$${volume}\:{of}\:{cap}=\pi{h}^{\mathrm{2}} \left({R}−\frac{{h}}{\mathrm{3}}\right)=\pi\left({R}−{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left({R}−\frac{{R}−{R}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{3}}\right) \\ $$$$=\frac{\pi}{\mathrm{3}}{R}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\frac{\pi{R}^{\mathrm{3}} }{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)+\frac{\pi}{\mathrm{3}}{R}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{3sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)+\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)=\mathrm{4} \\ $$$$\mathrm{3}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)\left(\mathrm{1}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)+\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)=\mathrm{4} \\ $$$$\left(\mathrm{1}−\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right)\left(\mathrm{cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}+\mathrm{4}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}+\mathrm{7}\right)=\mathrm{4} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\approx\mathrm{0}.\mathrm{5874} \\ $$$$\Rightarrow\alpha\approx\mathrm{108}.\mathrm{05}° \\ $$
Commented by ajfour last updated on 09/Sep/18

$${yes}\:{sir}.\:{Thanks}. \\ $$
