Question Number 43319 by Meritguide1234 last updated on 09/Sep/18
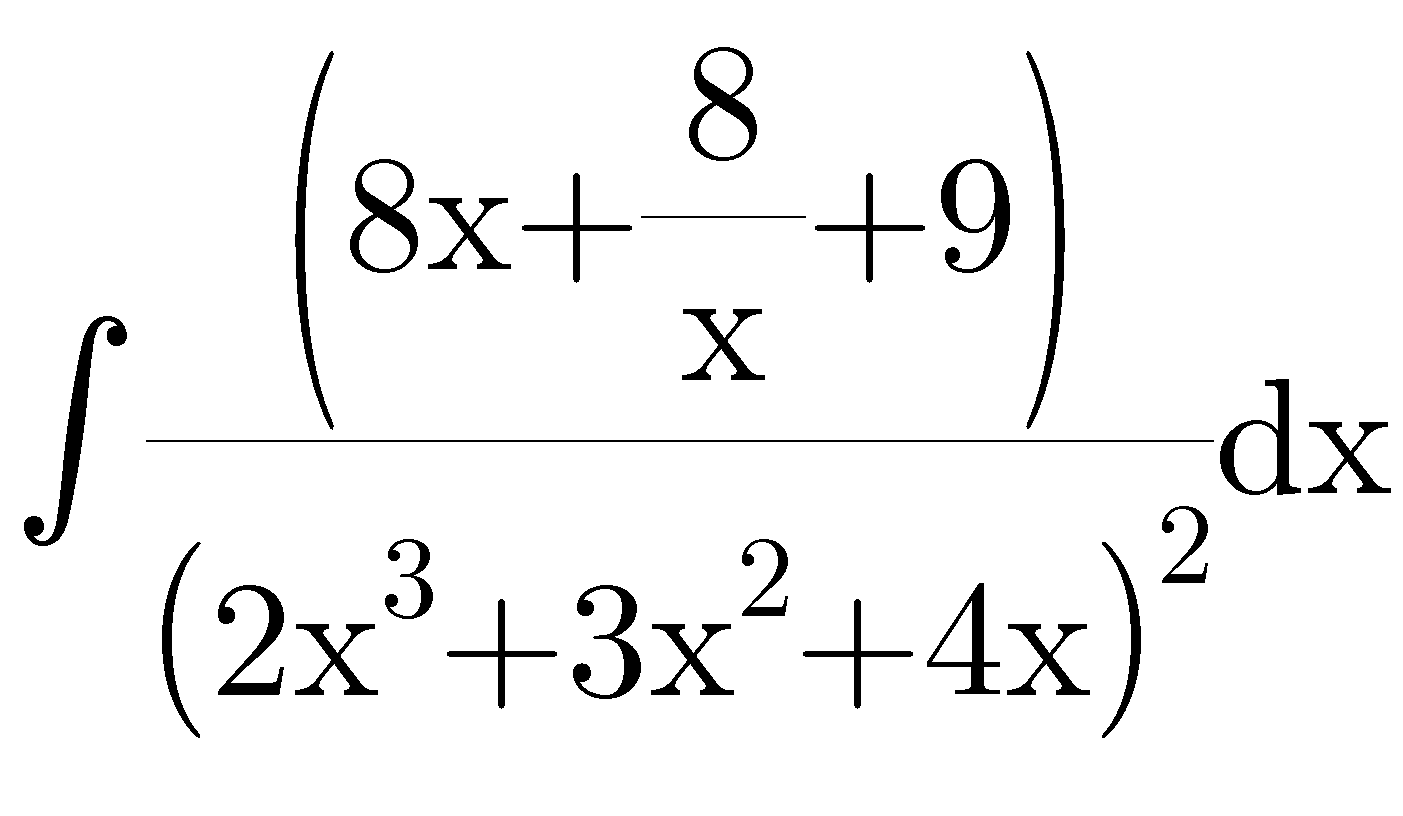
Answered by MJS last updated on 09/Sep/18
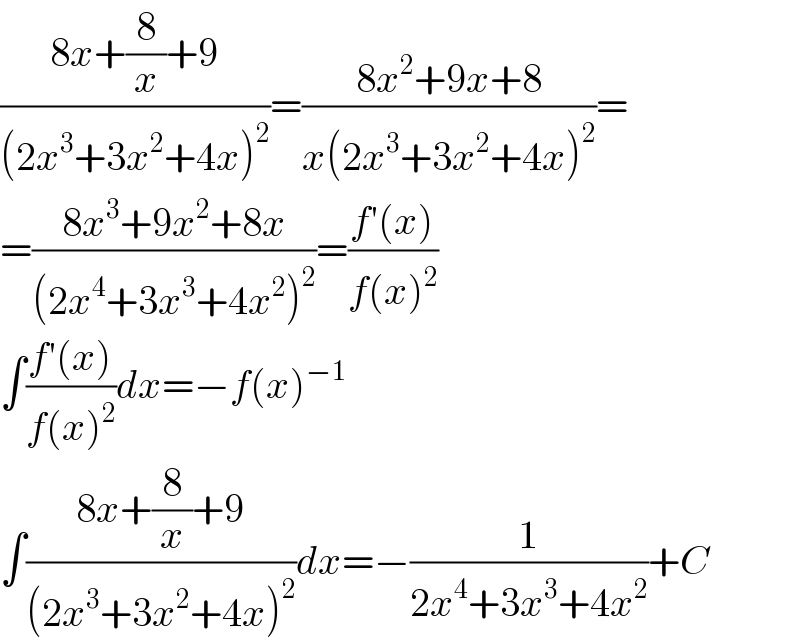
$$\frac{\mathrm{8}{x}+\frac{\mathrm{8}}{{x}}+\mathrm{9}}{\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}\right)^{\mathrm{2}} }=\frac{\mathrm{8}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{8}}{{x}\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} +\mathrm{8}{x}}{\left(\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{{f}'\left({x}\right)}{{f}\left({x}\right)^{\mathrm{2}} } \\ $$$$\int\frac{{f}'\left({x}\right)}{{f}\left({x}\right)^{\mathrm{2}} }{dx}=−{f}\left({x}\right)^{−\mathrm{1}} \\ $$$$\int\frac{\mathrm{8}{x}+\frac{\mathrm{8}}{{x}}+\mathrm{9}}{\left(\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} }+{C} \\ $$
Commented by Meritguide1234 last updated on 10/Sep/18
$${thank}\:{you} \\ $$
