Question Number 43324 by Raj Singh last updated on 09/Sep/18

Answered by tanmay.chaudhury50@gmail.com last updated on 09/Sep/18
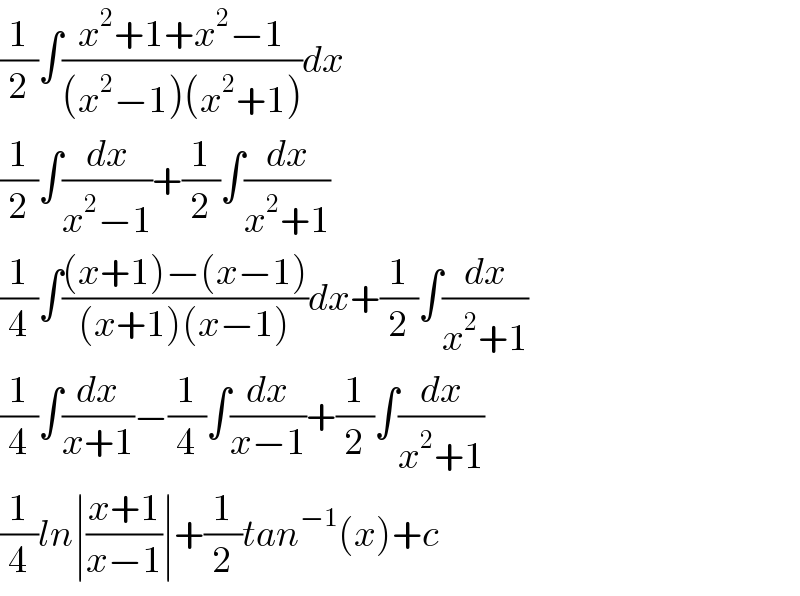
$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} +\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left({x}\right)+{c} \\ $$
