Question Number 43360 by ajfour last updated on 10/Sep/18

Commented by ajfour last updated on 10/Sep/18

$${Find}\:\boldsymbol{{R}}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}. \\ $$
Commented by ajfour last updated on 10/Sep/18
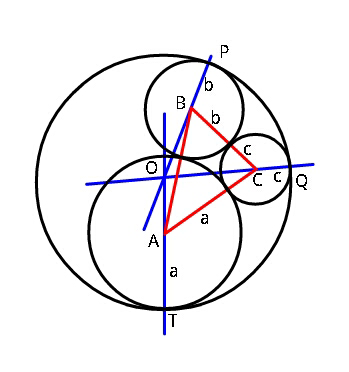
Commented by ajfour last updated on 10/Sep/18

$${please}\:{help}.. \\ $$
Commented by MJS last updated on 10/Sep/18

$$\mathrm{same}\:\mathrm{as}\:\mathrm{question}\:\mathrm{37209} \\ $$
Commented by ajfour last updated on 10/Sep/18

$${Thanks}\:{again}\:{Sir},\:{the}\:{solution} \\ $$$${there}\:{is}\:{not}\:{legible},\:{plus}\:{pretty} \\ $$$${lengthy}\:{it}\:{is}.\:{I}\:{have}\:{not}\:{understood} \\ $$$${solving}\:{it}\:{yet}.\: \\ $$
Commented by MJS last updated on 10/Sep/18

$$\mathrm{start}\:\mathrm{with}\:{A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:\:\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{{a}+{b}}\end{pmatrix} \\ $$$$\mathrm{then}\:\mathrm{calculate}\:{C}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix} \\ $$$$\mid{AC}\mid^{\mathrm{2}} =\left({a}+{c}\right)^{\mathrm{2}} \\ $$$$\mid{BC}\mid^{\mathrm{2}} =\left({b}+{c}\right)^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:{x}\:\mathrm{and}\:{y} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{2}\:\mathrm{solutions},\:\mathrm{one}\:\mathrm{with}\:{x}<\mathrm{0},\:\mathrm{the}\:\mathrm{other} \\ $$$$\mathrm{with}\:{x}>\mathrm{0} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{depends}\:\mathrm{on}\:{c} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{if}\:{c}\:\mathrm{is}\:\mathrm{very}\:\mathrm{small},\:\mathrm{the}\:“\mathrm{circumcircle}''\:\mathrm{touches} \\ $$$$\mathrm{the}\:\mathrm{three}\:\mathrm{circles}\:\mathrm{from}\:\mathrm{outside} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{there}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{value}\:\mathrm{of}\:{c}\:\mathrm{so}\:\mathrm{that}\:\mathrm{the} \\ $$$$“\mathrm{circumcircle}''\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:=\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{tangent}\:\mathrm{to}\:\mathrm{the}\:\mathrm{three}\:\mathrm{circles} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{if}\:{c}\:\mathrm{is}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{this}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:“\mathrm{usual}'' \\ $$$$\mathrm{commoncircle} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{all}\:\mathrm{circles}\:\mathrm{touching}\:\mathrm{circles}\:\mathrm{a\&b} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{d}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{common} \\ $$$$\mathrm{point}\:\mathrm{with}\:\mathrm{circle}\:\mathrm{c} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{circles}\:\mathrm{touching}\:\mathrm{circles}\:\mathrm{a\&b}\:\mathrm{from}\:\mathrm{outside} \\ $$$$\mathrm{with}\:\mathrm{center}\:{D}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix} \\ $$$$\mid{AD}\mid^{\mathrm{2}} =\left({a}+{d}\right)^{\mathrm{2}} \\ $$$$\mid{BD}\mid^{\mathrm{2}} =\left({b}+{d}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{common}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{circles}\:\mathrm{a\&b} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:\mathrm{circumcircles}\:\mathrm{of}\:\mathrm{circles}\:\mathrm{a\&b} \\ $$$$\mathrm{with}\:\mathrm{center}\:{D}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix} \\ $$$$\mid{AD}\mid^{\mathrm{2}} =\left({d}−{a}\right)^{\mathrm{2}} \\ $$$$\mid{BD}\mid^{\mathrm{2}} =\left({d}−{b}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{these}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{getting}\:\mathrm{longer}\:\mathrm{from}\:\mathrm{step} \\ $$$$\mathrm{to}\:\mathrm{step}\:\mathrm{but}\:\mathrm{that}'\mathrm{s}\:\mathrm{how}\:\mathrm{I}\:\mathrm{solved}\:\mathrm{it} \\ $$
Commented by MJS last updated on 10/Sep/18

$$\mathrm{you}\:\mathrm{mean}\:\mathrm{it}'\mathrm{s}\:\mathrm{technically}\:\mathrm{not}\:\mathrm{legible}\:\mathrm{or}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{because}\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{post}\:\mathrm{the}\:\mathrm{works},\:\mathrm{only}\:\mathrm{the} \\ $$$$\mathrm{results}? \\ $$
Commented by ajfour last updated on 11/Sep/18
![Centre of circles : A(0,−R+a) B[(a+b)cos θ, −R+a+(a+b)sin θ ] C[(a+c)cos φ, −R+a+(a+c)sin φ ] (a+b)^2 cos^2 θ+[−R+a+(a+b)sin θ]^2 = (R−b)^2 ...(i) (a+c)^2 cos^2 φ+[−R+a+(a+c)sin φ]^2 = (R−c)^2 ...(ii) [(a+b)cos θ−(a+c)cos φ]^2 +[(a+b)sin θ−(a+c)sin φ]^2 =(b+c)^2 ....(iii) ⇒ (a+b)^2 −2(R−a)(a+b)sin θ+(R−a)^2 = (R−b)^2 ⇒ sin 𝛉 = (((a+b)^2 +(R−a)^2 −(R−b)^2 )/(2(R−a)(a+b))) sin 𝛗 = (((a+c)^2 +(R−a)^2 −(R−c)^2 )/(2(R−a)(a+c))) ⇒ sin θ = ((a(a+b)−R(a−b))/(R(a+b)−a(a+b))) ⇒ sin φ = ((a(a+c)−R(a−c))/(R(a+c)−a(a+c))) ⇒ sin θ = (((a/R)−((a−b)/(a+b)))/(1−(a/R))) = ((x−p)/(1−x)) sin φ = (((a/R)−((a−c)/(a+c)))/(1−(a/R))) = ((x−q)/(1−x)) & Eq. (iii) again (a+b)^2 +(a+c)^2 −(b+c)^2 = 2(a+b)(a+c)cos (𝛉−𝛗) ⇒ (b−c)^2 −(b+c)^2 =− 2(a+b)(a+c)[1−cos (θ−φ)] ⇒ 1−cos (θ−φ)=((2bc)/((a+b)(a+c))) .....](https://www.tinkutara.com/question/Q43394.png)
$${Centre}\:\:{of}\:{circles}\:: \\ $$$$\:\:{A}\left(\mathrm{0},−{R}+{a}\right)\: \\ $$$$\:\:{B}\left[\left({a}+{b}\right)\mathrm{cos}\:\theta,\:−{R}+{a}+\left({a}+{b}\right)\mathrm{sin}\:\theta\:\right] \\ $$$$\:\:{C}\left[\left({a}+{c}\right)\mathrm{cos}\:\phi,\:−{R}+{a}+\left({a}+{c}\right)\mathrm{sin}\:\phi\:\right] \\ $$$$ \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+\left[−{R}+{a}+\left({a}+{b}\right)\mathrm{sin}\:\theta\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({R}−{b}\right)^{\mathrm{2}} \:\:\:\:\:\:\:…\left({i}\right) \\ $$$$\left({a}+{c}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \phi+\left[−{R}+{a}+\left({a}+{c}\right)\mathrm{sin}\:\phi\right]^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({R}−{c}\right)^{\mathrm{2}} \:\:\:\:\:\:…\left({ii}\right) \\ $$$$\left[\left({a}+{b}\right)\mathrm{cos}\:\theta−\left({a}+{c}\right)\mathrm{cos}\:\phi\right]^{\mathrm{2}} \: \\ $$$$+\left[\left({a}+{b}\right)\mathrm{sin}\:\theta−\left({a}+{c}\right)\mathrm{sin}\:\phi\right]^{\mathrm{2}} \:=\left({b}+{c}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({iii}\right) \\ $$$$\Rightarrow\:\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{2}\left({R}−{a}\right)\left({a}+{b}\right)\mathrm{sin}\:\theta+\left({R}−{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left({R}−{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\boldsymbol{\theta}\:=\:\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} +\left(\boldsymbol{{R}}−\boldsymbol{{a}}\right)^{\mathrm{2}} −\left(\boldsymbol{{R}}−\boldsymbol{{b}}\right)^{\mathrm{2}} }{\mathrm{2}\left(\boldsymbol{{R}}−\boldsymbol{{a}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)} \\ $$$$\:\:\:\mathrm{sin}\:\boldsymbol{\phi}\:=\:\frac{\left(\boldsymbol{{a}}+\boldsymbol{{c}}\right)^{\mathrm{2}} +\left(\boldsymbol{{R}}−\boldsymbol{{a}}\right)^{\mathrm{2}} −\left(\boldsymbol{{R}}−\boldsymbol{{c}}\right)^{\mathrm{2}} }{\mathrm{2}\left(\boldsymbol{{R}}−\boldsymbol{{a}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}\right)} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\:=\:\frac{{a}\left({a}+{b}\right)−{R}\left({a}−{b}\right)}{{R}\left({a}+{b}\right)−{a}\left({a}+{b}\right)} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\phi\:=\:\frac{{a}\left({a}+{c}\right)−{R}\left({a}−{c}\right)}{{R}\left({a}+{c}\right)−{a}\left({a}+{c}\right)} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\:=\:\frac{\frac{{a}}{{R}}−\frac{{a}−{b}}{{a}+{b}}}{\mathrm{1}−\frac{{a}}{{R}}}\:=\:\frac{{x}−{p}}{\mathrm{1}−{x}} \\ $$$$\:\:\:\:\:\mathrm{sin}\:\phi\:=\:\frac{\frac{{a}}{{R}}−\frac{{a}−{c}}{{a}+{c}}}{\mathrm{1}−\frac{{a}}{{R}}}\:=\:\frac{{x}−{q}}{\mathrm{1}−{x}} \\ $$$$\&\:\:\: \\ $$$$\boldsymbol{{Eq}}.\:\left(\boldsymbol{{iii}}\right)\:{again} \\ $$$$\:\:\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} +\left(\boldsymbol{{a}}+\boldsymbol{{c}}\right)^{\mathrm{2}} −\left(\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{2}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\left(\boldsymbol{{a}}+\boldsymbol{{c}}\right)\mathrm{cos}\:\left(\boldsymbol{\theta}−\boldsymbol{\phi}\right) \\ $$$$\Rightarrow\:\left({b}−{c}\right)^{\mathrm{2}} −\left({b}+{c}\right)^{\mathrm{2}} \\ $$$$\:\:\:=−\:\mathrm{2}\left({a}+{b}\right)\left({a}+{c}\right)\left[\mathrm{1}−\mathrm{cos}\:\left(\theta−\phi\right)\right] \\ $$$$\Rightarrow\:\mathrm{1}−\mathrm{cos}\:\left(\theta−\phi\right)=\frac{\mathrm{2}{bc}}{\left({a}+{b}\right)\left({a}+{c}\right)} \\ $$$$….. \\ $$
Commented by ajfour last updated on 10/Sep/18

$${will}\:{need}\:{to}\:{download}\:{and}\:{take} \\ $$$${printouts}\:\left({as}\:{i}\:{have}\:{a}\:{small}\:{screen}\:{phone}\right). \\ $$
