Question Number 43386 by ajfour last updated on 10/Sep/18
Commented by ajfour last updated on 10/Sep/18

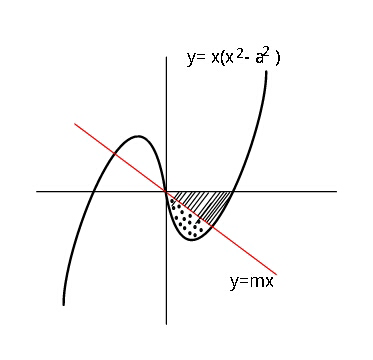
$${If}\:{the}\:{two}\:{differently}\:{shaded} \\ $$$${areas}\:{are}\:{equal},\:{find}\:{slope}\:\boldsymbol{{m}}\:{of} \\ $$$${line},\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}. \\ $$
Commented by Tawa1 last updated on 10/Sep/18
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{smoth}\:\mathrm{curve}\:\mathrm{using}\:\mathrm{lekh}\:\mathrm{diagram}\:? \\ $$
Commented by ajfour last updated on 10/Sep/18

$${quickly}\:{moved}\:{finger}\:{like}\:{a} \\ $$$${parabola}\:\left({one}\:{branch}\:{long},\:{other}\right. \\ $$$$\left.{short}\right),\:\left({lekh}\:{recognised}\:{it}\right), \\ $$$${copied}\:{it}\:,\:{flipped}\:{the}\:{copy} \\ $$$${verical}\:{then}\:{horizontal}\:{and} \\ $$$${joined}\:{the}\:{branch}\:{ends}\:{of}\: \\ $$$${original}\:{and}\:{copied}\:{one},\:{then} \\ $$$${grouped}\:{them},\:{then}\:{resized}\:{it}. \\ $$
Commented by Tawa1 last updated on 10/Sep/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MrW3 last updated on 10/Sep/18
![y=x(x^2 −a^2 ) (dy/dx)=3x^2 −a^2 at x=0: tan θ_0 =−a^2 ⇒r sin θ=r cos θ(r^2 cos^2 θ−a^2 ) ⇒r^2 =((tan θ+a^2 )/(cos^2 θ)) A=∫_θ_0 ^(2π) ((r^2 dθ)/2)=(1/2)∫_θ_0 ^(2π) ((tan θ+a^2 )/(cos^2 θ)) dθ =(1/2)∫_θ_0 ^(2π) (tan θ+a^2 ) d(tan θ) =(1/2)[((tan^2 θ)/2)+a^2 tan θ]_θ_0 ^(2π) =(1/2)[−(a^4 /2)+a^4 ]=(a^4 /4) let tan θ_1 =m A_1 =(1/2)[((tan^2 θ)/2)+a^2 tan θ]_θ_1 ^(2π) =(1/2)[−((tan^2 θ_1 )/2)−a^2 tan θ_1 ] =−(1/2)[(m^2 /2)+a^2 m]=(A/2)=(a^4 /8) ⇒2m^2 +4a^2 m+a^4 =0 ⇒m=((−4a^2 ±(√(16a^4 −8a^4 )))/4) = { ((−((2+(√2))/2)a^2 )),((−((2−(√2))/2)a^2 )) :} since ∣θ_1 ∣<∣θ_0 ∣⇒∣m∣=∣tan θ_1 ∣<∣tan θ_0 ∣=a^2 the suitable solution is: m=−((2−(√2))/2)a^2 ≈−0.293a^2](https://www.tinkutara.com/question/Q43399.png)
$${y}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$${at}\:{x}=\mathrm{0}:\:\mathrm{tan}\:\theta_{\mathrm{0}} =−{a}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow{r}\:\mathrm{sin}\:\theta={r}\:\mathrm{cos}\:\theta\left({r}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta−{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{\mathrm{tan}\:\theta+{a}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${A}=\int_{\theta_{\mathrm{0}} } ^{\mathrm{2}\pi} \frac{{r}^{\mathrm{2}} {d}\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\theta_{\mathrm{0}} } ^{\mathrm{2}\pi} \frac{\mathrm{tan}\:\theta+{a}^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta}\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\theta_{\mathrm{0}} } ^{\mathrm{2}\pi} \left(\mathrm{tan}\:\theta+{a}^{\mathrm{2}} \right)\:{d}\left(\mathrm{tan}\:\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{2}}+{a}^{\mathrm{2}} \mathrm{tan}\:\theta\right]_{\theta_{\mathrm{0}} } ^{\mathrm{2}\pi} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{{a}^{\mathrm{4}} }{\mathrm{2}}+{a}^{\mathrm{4}} \right]=\frac{{a}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${let}\:\mathrm{tan}\:\theta_{\mathrm{1}} ={m} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{2}}+{a}^{\mathrm{2}} \mathrm{tan}\:\theta\right]_{\theta_{\mathrm{1}} } ^{\mathrm{2}\pi} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{tan}^{\mathrm{2}} \:\theta_{\mathrm{1}} }{\mathrm{2}}−{a}^{\mathrm{2}} \mathrm{tan}\:\theta_{\mathrm{1}} \right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+{a}^{\mathrm{2}} {m}\right]=\frac{{A}}{\mathrm{2}}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{2}{m}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {m}+{a}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{m}=\frac{−\mathrm{4}{a}^{\mathrm{2}} \pm\sqrt{\mathrm{16}{a}^{\mathrm{4}} −\mathrm{8}{a}^{\mathrm{4}} }}{\mathrm{4}} \\ $$$$=\begin{cases}{−\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}{a}^{\mathrm{2}} }\\{−\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}{a}^{\mathrm{2}} }\end{cases} \\ $$$${since}\:\mid\theta_{\mathrm{1}} \mid<\mid\theta_{\mathrm{0}} \mid\Rightarrow\mid{m}\mid=\mid\mathrm{tan}\:\theta_{\mathrm{1}} \mid<\mid\mathrm{tan}\:\theta_{\mathrm{0}} \mid={a}^{\mathrm{2}} \\ $$$${the}\:{suitable}\:{solution}\:{is}: \\ $$$${m}=−\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}{a}^{\mathrm{2}} \approx−\mathrm{0}.\mathrm{293}{a}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 10/Sep/18
$${Thanks}\:{Sir},\:{i}\:{got}\:{the}\:{same}\:{answer}. \\ $$
Answered by ajfour last updated on 10/Sep/18
![Intersection points of line and curve: y=mx=x(x^2 −a^2 ) ⇒ O(0,0) and P ((√(a^2 +m)) , y_P ) A=−∫_0 ^( a) (x^3 −a^2 x)dx =−( (a^4 /4)−(a^4 /2)) ⇒ A=(a^4 /4) ∫_0 ^( (√(a^2 +m))) (mx−x^3 +a^2 x)dx = (a^4 /8) (=(A/2)) ⇒ ((m(a^2 +m))/2)−(((a^2 +m)^2 )/4)+((a^2 (a^2 +m))/2) = (a^4 /8) ⇒ (a^2 +m)^2 = (a^4 /2) ⇒ m= ((1/( (√2)))−1)a^2 same as m= −(((2−(√2))/2))a^2 . [ (dy/dx)∣_(x=0) = −a^2 ; so we reject m=−(1+(1/( (√2))))a^2 ].](https://www.tinkutara.com/question/Q43405.png)
$${Intersection}\:{points}\:{of}\:{line} \\ $$$${and}\:{curve}: \\ $$$${y}={mx}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{O}\left(\mathrm{0},\mathrm{0}\right)\:{and}\:{P}\:\left(\sqrt{{a}^{\mathrm{2}} +{m}}\:,\:{y}_{{P}} \right) \\ $$$${A}=−\int_{\mathrm{0}} ^{\:\:{a}} \left({x}^{\mathrm{3}} −{a}^{\mathrm{2}} {x}\right){dx}\:=−\left(\:\frac{{a}^{\mathrm{4}} }{\mathrm{4}}−\frac{{a}^{\mathrm{4}} }{\mathrm{2}}\right) \\ $$$$\Rightarrow\:{A}=\frac{{a}^{\mathrm{4}} }{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\:\:\sqrt{{a}^{\mathrm{2}} +{m}}} \left({mx}−{x}^{\mathrm{3}} +{a}^{\mathrm{2}} {x}\right){dx}\:=\:\frac{{a}^{\mathrm{4}} }{\mathrm{8}}\:\left(=\frac{{A}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\frac{{m}\left({a}^{\mathrm{2}} +{m}\right)}{\mathrm{2}}−\frac{\left({a}^{\mathrm{2}} +{m}\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{m}\right)}{\mathrm{2}}\:=\:\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$\Rightarrow\:\left({a}^{\mathrm{2}} +{m}\right)^{\mathrm{2}} =\:\frac{{a}^{\mathrm{4}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\boldsymbol{{m}}=\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)\boldsymbol{{a}}^{\mathrm{2}} \: \\ $$$${same}\:{as}\:\:\boldsymbol{{m}}=\:−\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\boldsymbol{{a}}^{\mathrm{2}} \:. \\ $$$$\left[\:\:\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{0}} \:=\:−{a}^{\mathrm{2}} \:;\:{so}\:{we}\:{reject}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}=−\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){a}^{\mathrm{2}} \:\:\right]. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18
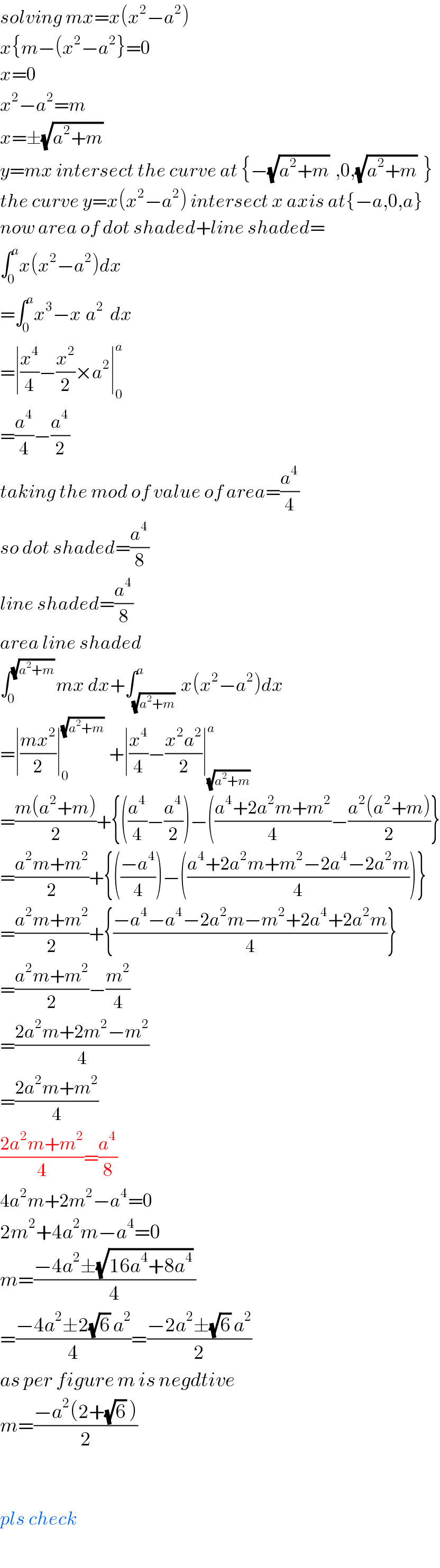
$${solving}\:{mx}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$${x}\left\{{m}−\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}=\mathrm{0}\right. \\ $$$${x}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{a}^{\mathrm{2}} ={m} \\ $$$${x}=\pm\sqrt{{a}^{\mathrm{2}} +{m}}\: \\ $$$${y}={mx}\:{intersect}\:{the}\:{curve}\:{at}\:\left\{−\sqrt{{a}^{\mathrm{2}} +{m}}\:\:,\mathrm{0},\sqrt{{a}^{\mathrm{2}} +{m}}\:\:\right\} \\ $$$${the}\:{curve}\:{y}={x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:{intersect}\:{x}\:{axis}\:{at}\left\{−{a},\mathrm{0},{a}\right\} \\ $$$${now}\:{area}\:{of}\:{dot}\:{shaded}+{line}\:{shaded}= \\ $$$$\int_{\mathrm{0}} ^{{a}} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{{a}} {x}^{\mathrm{3}} −{x}^{} {a}^{\mathrm{2}} \:\:{dx} \\ $$$$=\mid\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}×{a}^{\mathrm{2}} \mid_{\mathrm{0}} ^{{a}} \\ $$$$=\frac{{a}^{\mathrm{4}} }{\mathrm{4}}−\frac{{a}^{\mathrm{4}} }{\mathrm{2}}\: \\ $$$${taking}\:{the}\:{mod}\:{of}\:{value}\:{of}\:{area}=\frac{{a}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${so}\:{dot}\:{shaded}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$${line}\:{shaded}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$${area}\:{line}\:{shaded} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}\:} {mx}\:{dx}+\int_{\sqrt{{a}^{\mathrm{2}} +{m}}\:} ^{{a}} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){dx} \\ $$$$=\mid\frac{{mx}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}\:} \:+\mid\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{2}}\mid_{\sqrt{{a}^{\mathrm{2}} +{m}}\:} ^{{a}} \\ $$$$=\frac{{m}\left({a}^{\mathrm{2}} +{m}\right)}{\mathrm{2}}+\left\{\left(\frac{{a}^{\mathrm{4}} }{\mathrm{4}}−\frac{{a}^{\mathrm{4}} }{\mathrm{2}}\right)−\left(\frac{{a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{4}}−\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{m}\right)}{\mathrm{2}}\right\}\right. \\ $$$$=\frac{{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{2}}+\left\{\left(\frac{−{a}^{\mathrm{4}} }{\mathrm{4}}\right)−\left(\frac{{a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {m}}{\mathrm{4}}\right)\right\}\: \\ $$$$=\frac{{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{2}}+\left\{\frac{−{a}^{\mathrm{4}} −{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {m}−{m}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{2}} {m}}{\mathrm{4}}\right\} \\ $$$$=\frac{{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{2}}−\frac{{m}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} {m}+\mathrm{2}{m}^{\mathrm{2}} −{m}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\mathrm{2}{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{2}{a}^{\mathrm{2}} {m}+{m}^{\mathrm{2}} }{\mathrm{4}}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {m}+\mathrm{2}{m}^{\mathrm{2}} −{a}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{2}{m}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {m}−{a}^{\mathrm{4}} =\mathrm{0} \\ $$$${m}=\frac{−\mathrm{4}{a}^{\mathrm{2}} \pm\sqrt{\mathrm{16}{a}^{\mathrm{4}} +\mathrm{8}{a}^{\mathrm{4}} }\:}{\mathrm{4}} \\ $$$$=\frac{−\mathrm{4}{a}^{\mathrm{2}} \pm\mathrm{2}\sqrt{\mathrm{6}}\:{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{−\mathrm{2}{a}^{\mathrm{2}} \pm\sqrt{\mathrm{6}}\:{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${as}\:{per}\:{figure}\:{m}\:{is}\:{negdtive} \\ $$$${m}=\frac{−{a}^{\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{6}}\:\right)}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$${pls}\:{check} \\ $$
Commented by ajfour last updated on 10/Sep/18
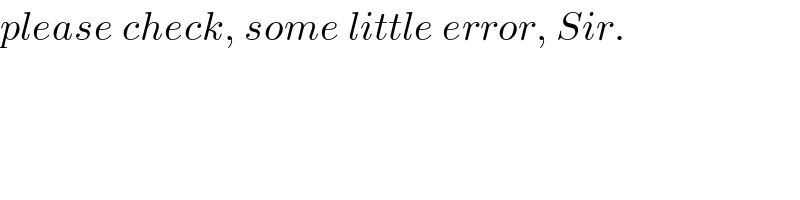
$${please}\:{check},\:{some}\:{little}\:{error},\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

$${i}\:{have}\:{done} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}\:} {mx}+\int_{\sqrt{{a}^{\mathrm{2}} +{m}}\:} ^{{a}} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){dx}\:{to}\:{find}\:{the}\:{line}\:{shaded} \\ $$$${area} \\ $$$${sum}\:{of}\:{the}\:{value}\:{of}\:{this}\:{two}\:{intregal}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$ \\ $$$${but}\:{you}\:{have}\:{done} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}\:} {mx}−{x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:{dx}=\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$${pls}\:{say}\:{which}\:{area}\:{belongs}\:{to}\:{this}\:{intregal} \\ $$
Commented by ajfour last updated on 10/Sep/18

$${the}\:{dot}\:{shaded}\:{area}\:{is}\:{equal}\:{to} \\ $$$${what}\:{i}\:{have}\:{integrated}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18
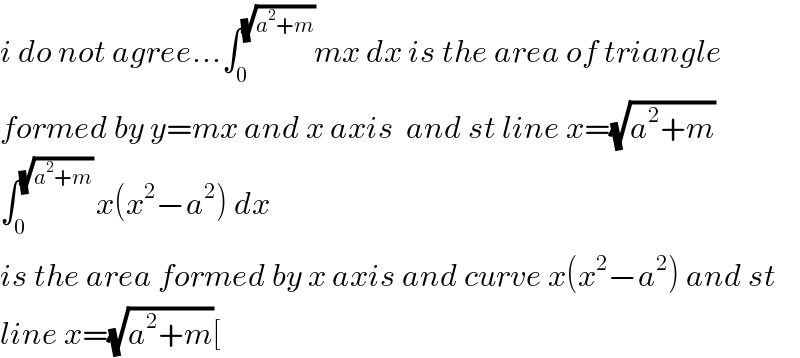
$${i}\:{do}\:{not}\:{agree}…\int_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}} {mx}\:{dx}\:{is}\:{the}\:{area}\:{of}\:{triangle} \\ $$$${formed}\:{by}\:{y}={mx}\:{and}\:{x}\:{axis}\:\:{and}\:{st}\:{line}\:{x}=\sqrt{{a}^{\mathrm{2}} +{m}}\: \\ $$$$\int_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} +{m}}\:} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:{dx} \\ $$$${is}\:{the}\:{area}\:{formed}\:{by}\:{x}\:{axis}\:{and}\:{curve}\:{x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\:{and}\:{st} \\ $$$${line}\:{x}=\sqrt{{a}^{\mathrm{2}} +{m}}\left[\:\right. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

$${pls}\:{find}\:{line}\:{shaded}\:{area}… \\ $$
Commented by ajfour last updated on 10/Sep/18
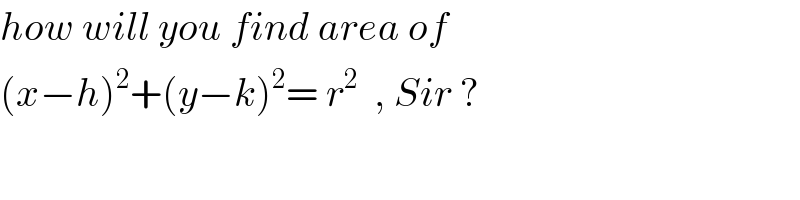
$${how}\:{will}\:{you}\:{find}\:{area}\:{of} \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} =\:{r}^{\mathrm{2}} \:\:,\:{Sir}\:? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18
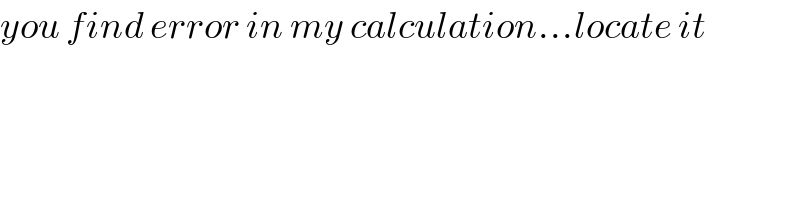
$${you}\:{find}\:{error}\:{in}\:{my}\:{calculation}…{locate}\:{it}\: \\ $$
Commented by ajfour last updated on 10/Sep/18
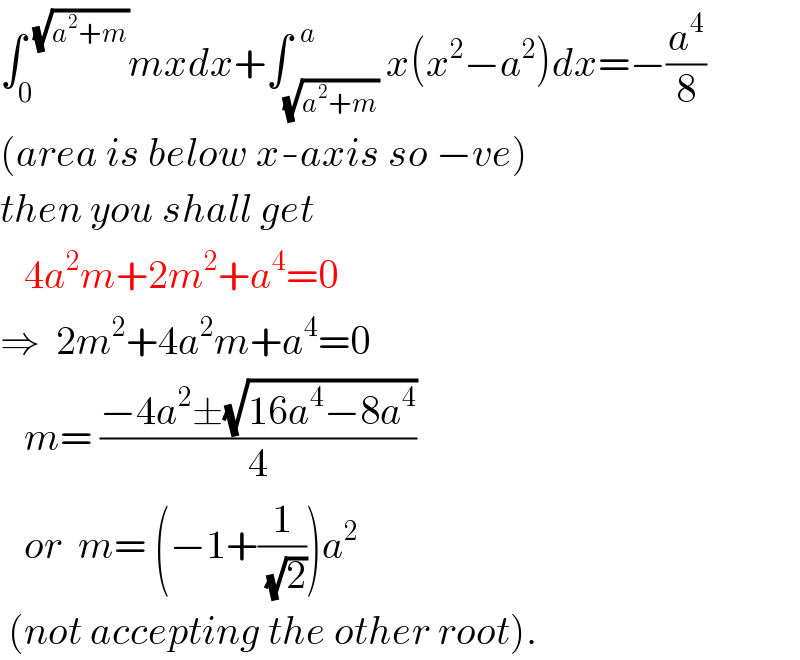
$$\int_{\mathrm{0}} ^{\:\:\sqrt{{a}^{\mathrm{2}} +{m}}} {mxdx}+\int_{\sqrt{{a}^{\mathrm{2}} +{m}}} ^{\:\:{a}} {x}\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){dx}=−\frac{{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$\left({area}\:{is}\:{below}\:{x}-{axis}\:{so}\:−{ve}\right) \\ $$$${then}\:{you}\:{shall}\:{get} \\ $$$$\:\:\:\mathrm{4}{a}^{\mathrm{2}} {m}+\mathrm{2}{m}^{\mathrm{2}} +{a}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{m}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {m}+{a}^{\mathrm{4}} =\mathrm{0} \\ $$$$\:\:\:{m}=\:\frac{−\mathrm{4}{a}^{\mathrm{2}} \pm\sqrt{\mathrm{16}{a}^{\mathrm{4}} −\mathrm{8}{a}^{\mathrm{4}} }}{\mathrm{4}} \\ $$$$\:\:\:{or}\:\:{m}=\:\left(−\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){a}^{\mathrm{2}} \:\:\: \\ $$$$\:\left({not}\:{accepting}\:{the}\:{other}\:{root}\right). \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Sep/18

$${ok}\:{thank}\:{you}… \\ $$
Answered by MJS last updated on 10/Sep/18
![p: y=x^3 −a^2 x l: y=mx p∩l x^3 −(m+a^2 )x=0 ⇒ x=(√(m+a^2 )) dotted area: D=∫_0 ^(√(m+a^2 )) (x^3 −a^2 x)dx−m∫_0 ^(√(m+a^2 )) xdx shaded area: S=m∫_0 ^(√(m+a^2 )) xdx+∫_( (√(m+a^2 ))) ^a (x^3 −a^2 x)dx D=(1/4)(m^2 −a^4 )−(1/2)m(m+a^2 )=−(1/4)(m+a^2 )^2 S=(1/2)m(m+a^2 )−(1/4)m^2 =(1/4)m(m+2a^2 ) S−D=0 m^2 +2a^2 m+(a^4 /2)=0 m=(−1+((√2)/2))a^2 [the 2^(nd) solution doesn′t give a real value for (√(m+a^2 ))]](https://www.tinkutara.com/question/Q43439.png)
$${p}:\:{y}={x}^{\mathrm{3}} −{a}^{\mathrm{2}} {x} \\ $$$${l}:\:{y}={mx} \\ $$$${p}\cap{l} \\ $$$${x}^{\mathrm{3}} −\left({m}+{a}^{\mathrm{2}} \right){x}=\mathrm{0}\:\Rightarrow\:{x}=\sqrt{{m}+{a}^{\mathrm{2}} } \\ $$$$\mathrm{dotted}\:\mathrm{area}:\:{D}=\underset{\mathrm{0}} {\overset{\sqrt{{m}+{a}^{\mathrm{2}} }} {\int}}\left({x}^{\mathrm{3}} −{a}^{\mathrm{2}} {x}\right){dx}−{m}\underset{\mathrm{0}} {\overset{\sqrt{{m}+{a}^{\mathrm{2}} }} {\int}}{xdx} \\ $$$$\mathrm{shaded}\:\mathrm{area}:\:{S}={m}\underset{\mathrm{0}} {\overset{\sqrt{{m}+{a}^{\mathrm{2}} }} {\int}}{xdx}+\underset{\:\sqrt{{m}+{a}^{\mathrm{2}} }} {\overset{{a}} {\int}}\left({x}^{\mathrm{3}} −{a}^{\mathrm{2}} {x}\right){dx} \\ $$$${D}=\frac{\mathrm{1}}{\mathrm{4}}\left({m}^{\mathrm{2}} −{a}^{\mathrm{4}} \right)−\frac{\mathrm{1}}{\mathrm{2}}{m}\left({m}+{a}^{\mathrm{2}} \right)=−\frac{\mathrm{1}}{\mathrm{4}}\left({m}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}{m}\left({m}+{a}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{4}}{m}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{m}\left({m}+\mathrm{2}{a}^{\mathrm{2}} \right) \\ $$$${S}−{D}=\mathrm{0} \\ $$$${m}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {m}+\frac{{a}^{\mathrm{4}} }{\mathrm{2}}=\mathrm{0} \\ $$$${m}=\left(−\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right){a}^{\mathrm{2}} \:\:\:\:\:\left[\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution}\:\mathrm{doesn}'\mathrm{t}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{give}\:\mathrm{a}\:\mathrm{real}\:\mathrm{value}\:\mathrm{for}\:\sqrt{{m}+{a}^{\mathrm{2}} }\right] \\ $$
