Menu Close

Question-43419

Tinku Tara 0 Comments
Pin




Question Number 43419 by Raj Singh last updated on 10/Sep/18
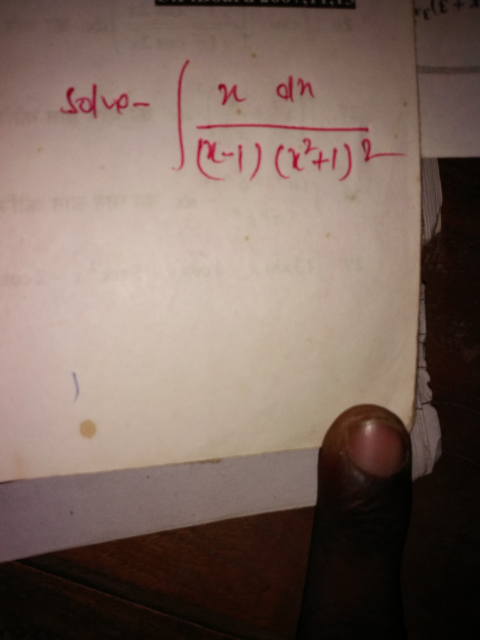
Commented by maxmathsup by imad last updated on 10/Sep/18
let A = ∫ ((xdx)/((x−1)(x^2 +1)^2 )) A = ∫ ((x−1+1)/((x−1)(x^2 +1)^2 ))dx = ∫ (dx/(x^2 +1)) + ∫ (dx/((x−1)(x^2 +1)^2 )) but ∫ (dx/(x^2 +1)) =arctanx +c_1 changemene x −1=t give ∫ (dx/((x−1)(x^2 +1)^2 )) = ∫ (dt/(t{ (t+1)^2 +1}^2 )) =_(t+1 =tanθ) ∫ (((1+tan^2 θ)dθ)/((tanθ−1){1+tan^2 θ}^2 )) = ∫ ((cos^2 θ)/(((sinθ)/(cosθ))−1)) dθ = ∫ ((cos^3 θ)/(sinθ −cosθ)) dθ = ∫ ((cos^3 θ)/( (√2)cos(θ +(π/4)))) dθ =_(θ +(π/4)=u) ∫ ((cos^3 (u−(π/4)))/( (√2)cosu)) du = ∫ (({((cosu)/( (√2)))+((sinu)/( (√2)))}^3 )/( (√2)cosu)) du = (1/4) ∫ (((cosu +sinu)^3 )/(cosu)) du =(1/4) ∫ ((cos^3 u +3cos^2 u sinu +3cosu sin^2 u +sin^3 u)/(cosu)) du =(1/4) ∫ cos^2 u du +(3/4) ∫ cosu sinu du +(3/4) ∫ sin^2 u du +(1/4) ∫ ((sin^3 u)/(cosu)) du =(1/8) ∫ (1+cos(2u)du +(3/8) ∫ sin(2u)du +(3/8) ∫ (1−cos(2u))du +(1/4) ∫((sin^3 u)/(cosu))du = (1/8) u +(1/(16))sin(2u) −(3/(16))cos(2u) +(3/8)u −(3/(16))sin(2u) +(1/4) ∫ (((1−cos^2 u)sinu)/(cosu))du u=θ +(π/4) =arctan(t+1) +(π/4) ....be contiued...
$${let}\:{A}\:=\:\int\:\:\frac{{xdx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${A}\:=\:\int\:\:\frac{{x}−\mathrm{1}+\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\:\int\:\:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{but} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:={arctanx}\:+{c}_{\mathrm{1}} \:\:\:\:{changemene}\:{x}\:−\mathrm{1}={t}\:{give} \\ $$$$\int\:\:\:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\:\int\:\:\:\frac{{dt}}{{t}\left\{\:\left({t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}^{\mathrm{2}} }\:=_{{t}+\mathrm{1}\:={tan}\theta} \:\:\:\:\:\int\:\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\left({tan}\theta−\mathrm{1}\right)\left\{\mathrm{1}+{tan}^{\mathrm{2}} \theta\right\}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\:\frac{{cos}^{\mathrm{2}} \theta}{\frac{{sin}\theta}{{cos}\theta}−\mathrm{1}}\:{d}\theta\:=\:\int\:\:\:\frac{{cos}^{\mathrm{3}} \theta}{{sin}\theta\:−{cos}\theta}\:{d}\theta\:=\:\int\:\:\frac{{cos}^{\mathrm{3}} \theta}{\:\sqrt{\mathrm{2}}{cos}\left(\theta\:+\frac{\pi}{\mathrm{4}}\right)}\:{d}\theta \\ $$$$=_{\theta\:+\frac{\pi}{\mathrm{4}}={u}} \:\:\:\:\:\int\:\:\:\frac{{cos}^{\mathrm{3}} \left({u}−\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}{cosu}}\:{du}\:=\:\int\:\:\:\frac{\left\{\frac{{cosu}}{\:\sqrt{\mathrm{2}}}+\frac{{sinu}}{\:\sqrt{\mathrm{2}}}\right\}^{\mathrm{3}} }{\:\sqrt{\mathrm{2}}{cosu}}\:{du} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\:\:\:\frac{\left({cosu}\:+{sinu}\right)^{\mathrm{3}} }{{cosu}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\:\:\frac{{cos}^{\mathrm{3}} {u}\:+\mathrm{3}{cos}^{\mathrm{2}} {u}\:{sinu}\:+\mathrm{3}{cosu}\:{sin}^{\mathrm{2}} {u}\:+{sin}^{\mathrm{3}} {u}}{{cosu}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\:\int\:\:{cos}^{\mathrm{2}} {u}\:{du}\:\:+\frac{\mathrm{3}}{\mathrm{4}}\:\int\:{cosu}\:{sinu}\:{du}\:\:+\frac{\mathrm{3}}{\mathrm{4}}\:\int\:{sin}^{\mathrm{2}} {u}\:{du}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\frac{{sin}^{\mathrm{3}} {u}}{{cosu}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int\:\:\left(\mathrm{1}+{cos}\left(\mathrm{2}{u}\right){du}\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int\:{sin}\left(\mathrm{2}{u}\right){du}\:\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int\:\left(\mathrm{1}−{cos}\left(\mathrm{2}{u}\right)\right){du}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int\frac{{sin}^{\mathrm{3}} {u}}{{cosu}}{du}\right. \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:{u}\:+\frac{\mathrm{1}}{\mathrm{16}}{sin}\left(\mathrm{2}{u}\right)\:−\frac{\mathrm{3}}{\mathrm{16}}{cos}\left(\mathrm{2}{u}\right)\:+\frac{\mathrm{3}}{\mathrm{8}}{u}\:−\frac{\mathrm{3}}{\mathrm{16}}{sin}\left(\mathrm{2}{u}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\frac{\left(\mathrm{1}−{cos}^{\mathrm{2}} {u}\right){sinu}}{{cosu}}{du} \\ $$$${u}=\theta\:+\frac{\pi}{\mathrm{4}}\:={arctan}\left({t}+\mathrm{1}\right)\:+\frac{\pi}{\mathrm{4}}\:….{be}\:{contiued}… \\ $$
Commented by maxmathsup by imad last updated on 10/Sep/18
another way for the integral ∫ (dx/((x−1)(x^2 +1)^2 )) we decompose the fraction F(x) = (1/((x−1)(x^2 +1)^2 )) F(x) =(a/(x−1)) +((bx+c)/(x^2 +1)) +((dx +e)/((x^2 +1)^2 )) a=lim_(x→1) (x−1)F(x) =(1/2) lim_(x→+∞) x F(x) =0 =a+b ⇒b=−(1/2) ⇒ F(x) = (1/(2(x−1))) −(1/2) ((x−2c)/(x^2 +1)) + ((dx+e)/((x^2 +1)^2 )) we have F(0) =−1 =−(1/2) +c +e ⇒c+e =−(1/2) F(2)= (1/2) −(1/2) ((2−2c)/5) + ((2d +e)/(25)) =(1/(25)) F(−1) = −(1/8) =−(1/4) −(1/2) ((−1−2c)/2) +((−d +e)/4) weget a linear system with unknown c ,d,e ....
$${another}\:{way}\:{for}\:{the}\:{integral}\:\:\int\:\:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{we}\:{decompose}\:{the}\: \\ $$$${fraction}\:{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)\:=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{dx}\:+{e}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${a}={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lim}_{{x}\rightarrow+\infty} {x}\:{F}\left({x}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\frac{{x}−\mathrm{2}{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\:\frac{{dx}+{e}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\:{we}\:{have} \\ $$$${F}\left(\mathrm{0}\right)\:=−\mathrm{1}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:+{c}\:+{e}\:\Rightarrow{c}+{e}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left(\mathrm{2}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{2}−\mathrm{2}{c}}{\mathrm{5}}\:+\:\frac{\mathrm{2}{d}\:+{e}}{\mathrm{25}}\:=\frac{\mathrm{1}}{\mathrm{25}} \\ $$$${F}\left(−\mathrm{1}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{8}}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{−\mathrm{1}−\mathrm{2}{c}}{\mathrm{2}}\:+\frac{−{d}\:+{e}}{\mathrm{4}}\:\:{weget}\:{a}\:{linear}\:{system}\:{with}\:{unknown} \\ $$$${c}\:,{d},{e}\:…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *