Question Number 43449 by ajfour last updated on 10/Sep/18
Answered by MJS last updated on 10/Sep/18
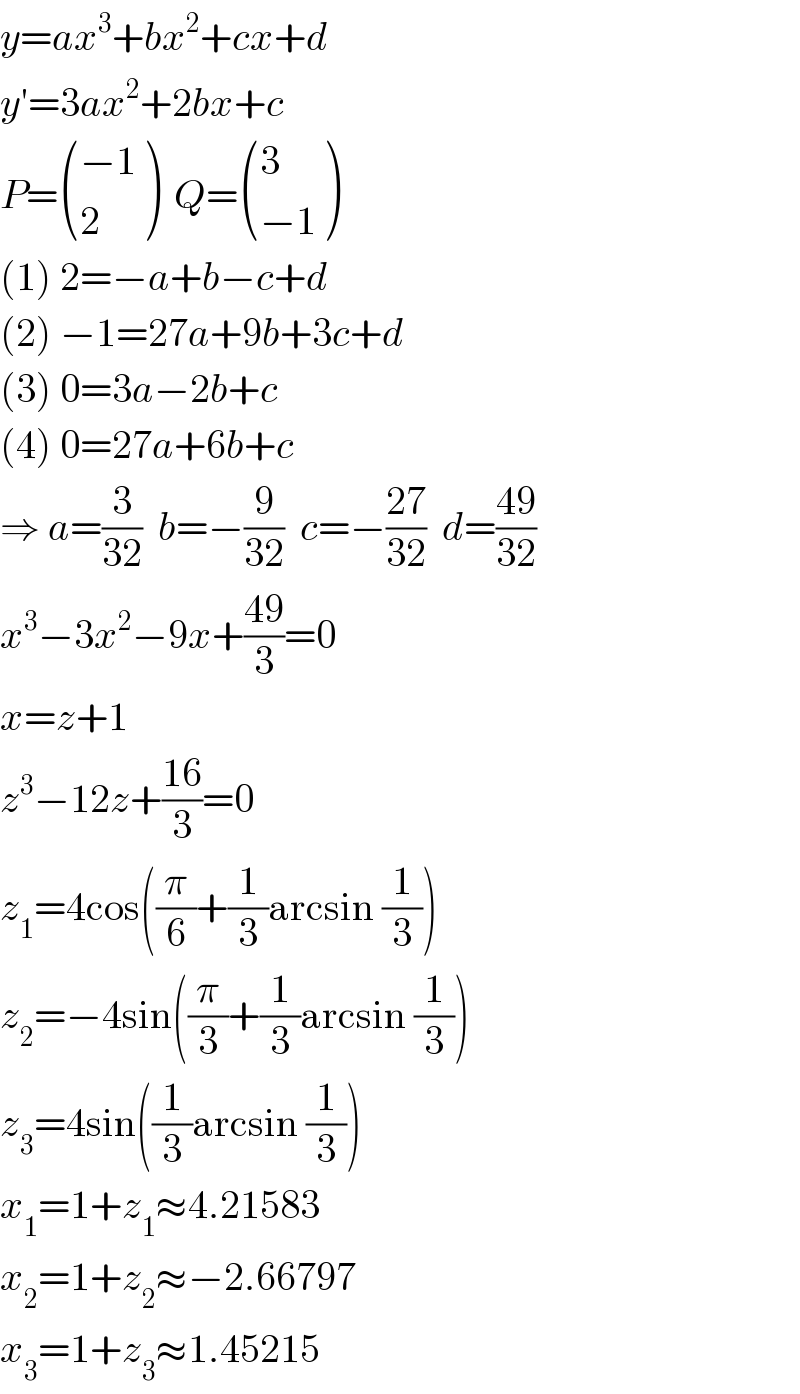
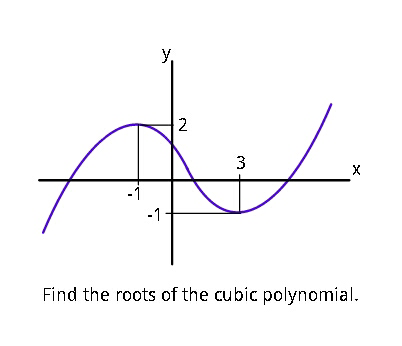
$${y}={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${y}'=\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c} \\ $$$${P}=\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{2}}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{\mathrm{3}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}=−{a}+{b}−{c}+{d} \\ $$$$\left(\mathrm{2}\right)\:−\mathrm{1}=\mathrm{27}{a}+\mathrm{9}{b}+\mathrm{3}{c}+{d} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{0}=\mathrm{3}{a}−\mathrm{2}{b}+{c} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{0}=\mathrm{27}{a}+\mathrm{6}{b}+{c} \\ $$$$\Rightarrow\:{a}=\frac{\mathrm{3}}{\mathrm{32}}\:\:{b}=−\frac{\mathrm{9}}{\mathrm{32}}\:\:{c}=−\frac{\mathrm{27}}{\mathrm{32}}\:\:{d}=\frac{\mathrm{49}}{\mathrm{32}} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{9}{x}+\frac{\mathrm{49}}{\mathrm{3}}=\mathrm{0} \\ $$$${x}={z}+\mathrm{1} \\ $$$${z}^{\mathrm{3}} −\mathrm{12}{z}+\frac{\mathrm{16}}{\mathrm{3}}=\mathrm{0} \\ $$$${z}_{\mathrm{1}} =\mathrm{4cos}\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${z}_{\mathrm{2}} =−\mathrm{4sin}\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${z}_{\mathrm{3}} =\mathrm{4sin}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${x}_{\mathrm{1}} =\mathrm{1}+{z}_{\mathrm{1}} \approx\mathrm{4}.\mathrm{21583} \\ $$$${x}_{\mathrm{2}} =\mathrm{1}+{z}_{\mathrm{2}} \approx−\mathrm{2}.\mathrm{66797} \\ $$$${x}_{\mathrm{3}} =\mathrm{1}+{z}_{\mathrm{3}} \approx\mathrm{1}.\mathrm{45215} \\ $$
Commented by ajfour last updated on 10/Sep/18

$${Marvelous}\:{Sir},\:{i}\:{got}\:{the}\:{same} \\ $$$${cubic}\:{equation}\:\left({couldn}'{t}\:{express}\right. \\ $$$$\left.{the}\:{roots}\right).\:{Thanks}. \\ $$
Commented by MJS last updated on 10/Sep/18
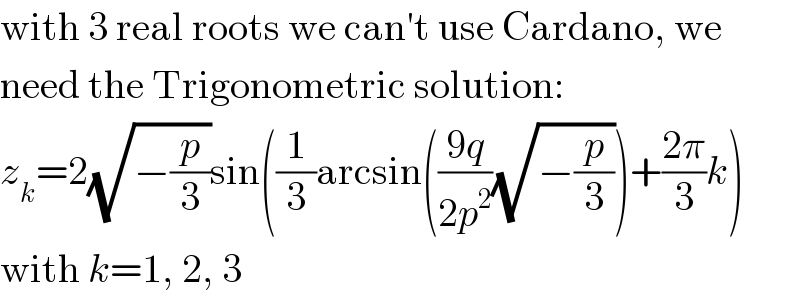
$$\mathrm{with}\:\mathrm{3}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{use}\:\mathrm{Cardano},\:\mathrm{we} \\ $$$$\mathrm{need}\:\mathrm{the}\:\mathrm{Trigonometric}\:\mathrm{solution}: \\ $$$${z}_{{k}} =\mathrm{2}\sqrt{−\frac{{p}}{\mathrm{3}}}\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\left(\frac{\mathrm{9}{q}}{\mathrm{2}{p}^{\mathrm{2}} }\sqrt{−\frac{{p}}{\mathrm{3}}}\right)+\frac{\mathrm{2}\pi}{\mathrm{3}}{k}\right) \\ $$$$\mathrm{with}\:{k}=\mathrm{1},\:\mathrm{2},\:\mathrm{3} \\ $$
Commented by ajfour last updated on 10/Sep/18
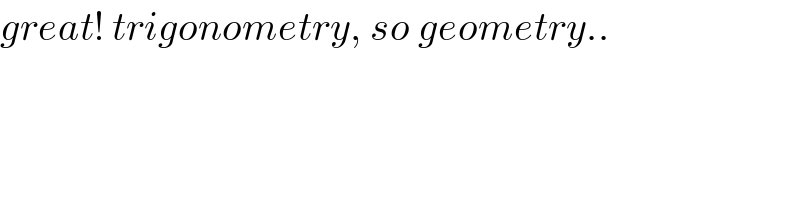
$${great}!\:{trigonometry},\:{so}\:{geometry}.. \\ $$
