Menu Close

Question-43517

Tinku Tara 0 Comments
Pin




Question Number 43517 by Raj Singh last updated on 11/Sep/18
Commented by maxmathsup by imad last updated on 11/Sep/18
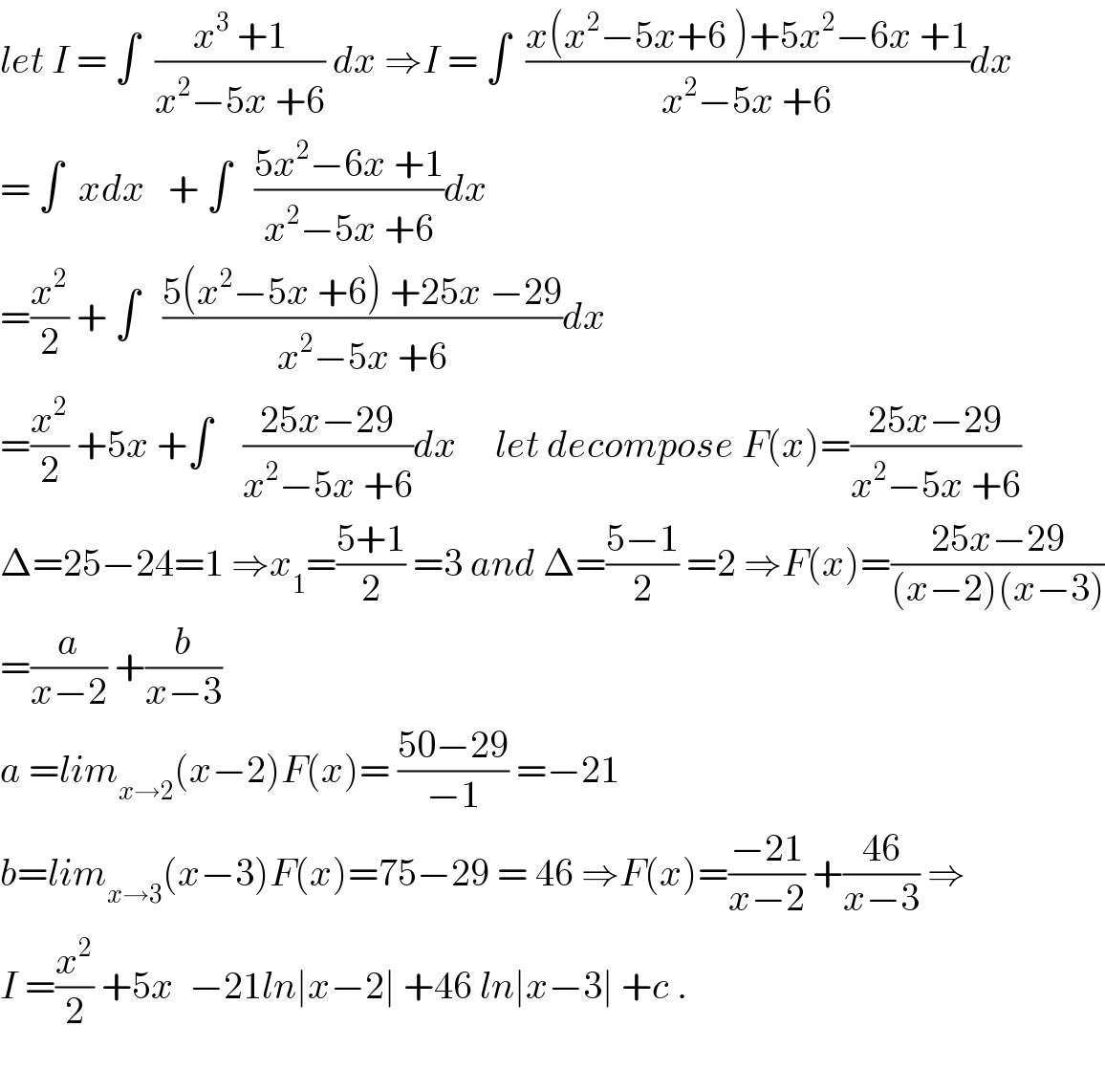
let I = ∫ ((x^3 +1)/(x^2 −5x +6)) dx ⇒I = ∫ ((x(x^2 −5x+6 )+5x^2 −6x +1)/(x^2 −5x +6))dx = ∫ xdx + ∫ ((5x^2 −6x +1)/(x^2 −5x +6))dx =(x^2 /2) + ∫ ((5(x^2 −5x +6) +25x −29)/(x^2 −5x +6))dx =(x^2 /2) +5x +∫ ((25x−29)/(x^2 −5x +6))dx let decompose F(x)=((25x−29)/(x^2 −5x +6)) Δ=25−24=1 ⇒x_1 =((5+1)/2) =3 and Δ=((5−1)/2) =2 ⇒F(x)=((25x−29)/((x−2)(x−3))) =(a/(x−2)) +(b/(x−3)) a =lim_(x→2) (x−2)F(x)= ((50−29)/(−1)) =−21 b=lim_(x→3) (x−3)F(x)=75−29 = 46 ⇒F(x)=((−21)/(x−2)) +((46)/(x−3)) ⇒ I =(x^2 /2) +5x −21ln∣x−2∣ +46 ln∣x−3∣ +c .
$${let}\:{I}\:=\:\int\:\:\frac{{x}^{\mathrm{3}} \:+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}}\:{dx}\:\Rightarrow{I}\:=\:\int\:\:\frac{{x}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}\:\right)+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}}{dx} \\ $$$$=\:\int\:\:{xdx}\:\:\:+\:\int\:\:\:\frac{\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}}{dx} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\:\int\:\:\:\frac{\mathrm{5}\left({x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}\right)\:+\mathrm{25}{x}\:−\mathrm{29}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}}{dx} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{5}{x}\:+\int\:\:\:\:\frac{\mathrm{25}{x}−\mathrm{29}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}}{dx}\:\:\:\:\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{25}{x}−\mathrm{29}}{{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\mathrm{6}} \\ $$$$\Delta=\mathrm{25}−\mathrm{24}=\mathrm{1}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{3}\:{and}\:\Delta=\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{25}{x}−\mathrm{29}}{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)} \\ $$$$=\frac{{a}}{{x}−\mathrm{2}}\:+\frac{{b}}{{x}−\mathrm{3}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{2}} \left({x}−\mathrm{2}\right){F}\left({x}\right)=\:\frac{\mathrm{50}−\mathrm{29}}{−\mathrm{1}}\:=−\mathrm{21} \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{3}} \left({x}−\mathrm{3}\right){F}\left({x}\right)=\mathrm{75}−\mathrm{29}\:=\:\mathrm{46}\:\Rightarrow{F}\left({x}\right)=\frac{−\mathrm{21}}{{x}−\mathrm{2}}\:+\frac{\mathrm{46}}{{x}−\mathrm{3}}\:\Rightarrow \\ $$$${I}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{5}{x}\:\:−\mathrm{21}{ln}\mid{x}−\mathrm{2}\mid\:+\mathrm{46}\:{ln}\mid{x}−\mathrm{3}\mid\:+{c}\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *