Question Number 43544 by behi83417@gmail.com last updated on 11/Sep/18
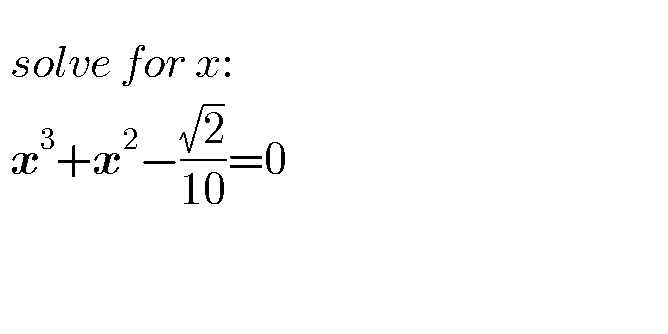
Answered by MJS last updated on 12/Sep/18

$${x}={z}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{3}}{z}+\frac{\mathrm{2}}{\mathrm{27}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{10}}=\mathrm{0} \\ $$$$\mathrm{trigonometric}\:\mathrm{solution}\:\mathrm{method} \\ $$$${z}_{{k}} =\mathrm{2}\sqrt{−\frac{{p}}{\mathrm{3}}}\mathrm{sin}\left(\frac{\mathrm{2}\pi{k}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\left(\frac{\mathrm{9}{q}}{\mathrm{2}{p}^{\mathrm{2}} }\sqrt{−\frac{{p}}{\mathrm{3}}}\right)\right) \\ $$$${x}_{{k}} ={z}_{{k}} −\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${x}_{\mathrm{1}} \approx.\mathrm{326514} \\ $$$${x}_{\mathrm{2}} \approx−.\mathrm{745626} \\ $$$${x}_{\mathrm{3}} \approx−.\mathrm{580888} \\ $$
Commented by behi83417@gmail.com last updated on 12/Sep/18
$${thanks}\:{in}\:{advance}\:{sir}. \\ $$
