Question Number 43571 by rahul 19 last updated on 12/Sep/18

Answered by ajfour last updated on 21/Sep/18
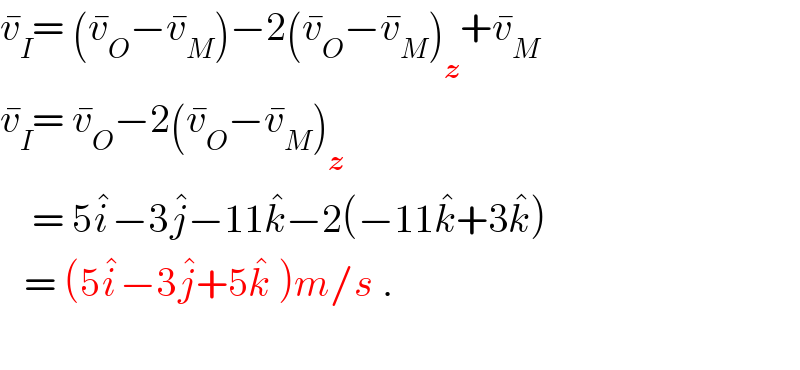
$$\bar {{v}}_{{I}} =\:\left(\bar {{v}}_{{O}} −\bar {{v}}_{{M}} \right)−\mathrm{2}\left(\bar {{v}}_{{O}} −\bar {{v}}_{{M}} \right)_{\boldsymbol{{z}}} +\bar {{v}}_{{M}} \\ $$$$\bar {{v}}_{{I}} =\:\bar {{v}}_{{O}} −\mathrm{2}\left(\bar {{v}}_{{O}} −\bar {{v}}_{{M}} \right)_{\boldsymbol{{z}}} \\ $$$$\:\:\:\:=\:\mathrm{5}\hat {{i}}−\mathrm{3}\hat {{j}}−\mathrm{11}\hat {{k}}−\mathrm{2}\left(−\mathrm{11}\hat {{k}}+\mathrm{3}\hat {{k}}\right) \\ $$$$\:\:\:=\:\left(\mathrm{5}\hat {{i}}−\mathrm{3}\hat {{j}}+\mathrm{5}\hat {{k}}\:\right){m}/{s}\:. \\ $$$$\: \\ $$
Commented by rahul 19 last updated on 15/Sep/18

$$\:\mathrm{why}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{image}\:\mathrm{in}\:{x\&}\mathrm{y} \\ $$$$\mathrm{plane}\:\mathrm{remained}\:\mathrm{same}\:\mathrm{as}\:\mathrm{that}\:\mathrm{of}\:\mathrm{object}?? \\ $$
Commented by ajfour last updated on 21/Sep/18

$${from}\:{a}\:{mirror}\:{parallel}\:{to}\:{x}-{y} \\ $$$${plane}\:{only}\:{the}\:{v}_{{z}} \:\:{of} \\ $$$${image}\:{can}\:{undergo}\:{a}\:{change}, \\ $$$$\left({think}\:{yourself},\:{obvious}\:{but}\right. \\ $$$${difficult}\:{for}\:{me}\:{to}\:{explain},\:{i} \\ $$$$\left.{haven}'{t}\:{even}\:{used}\:{this}\:{fact}\right). \\ $$
Commented by rahul 19 last updated on 21/Sep/18

$${I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{how}\:\mathrm{mirror}\:\mathrm{is}\:\mathrm{parallel} \\ $$$$\mathrm{to}\:{x}−{y}\:\mathrm{plane}?\:\mathrm{I}{n}\:\mathrm{the}\:\mathrm{ques}.\:\mathrm{it}\:\mathrm{has}\: \\ $$$$\mathrm{velocity}\:\mathrm{in}\:\mathrm{all}\:\mathrm{3}\:\mathrm{perpendicular}\:\mathrm{a}{x}\mathrm{es}! \\ $$
Commented by ajfour last updated on 21/Sep/18

$${linear}\:{velocity}\:{has}\:{nothing}\:{to}\:{do} \\ $$$${with}\:{orientation}\:\left({here}\right). \\ $$
Commented by rahul 19 last updated on 21/Sep/18

$${ok}\:{sir},\:{thanks}! \\ $$
