Menu Close

Question-43657

Tinku Tara 0 Comments
Pin




Question Number 43657 by Tinkutara last updated on 13/Sep/18
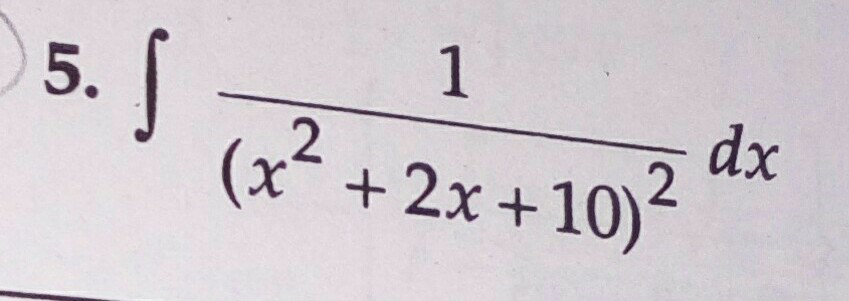
Commented by maxmathsup by imad last updated on 24/Sep/18
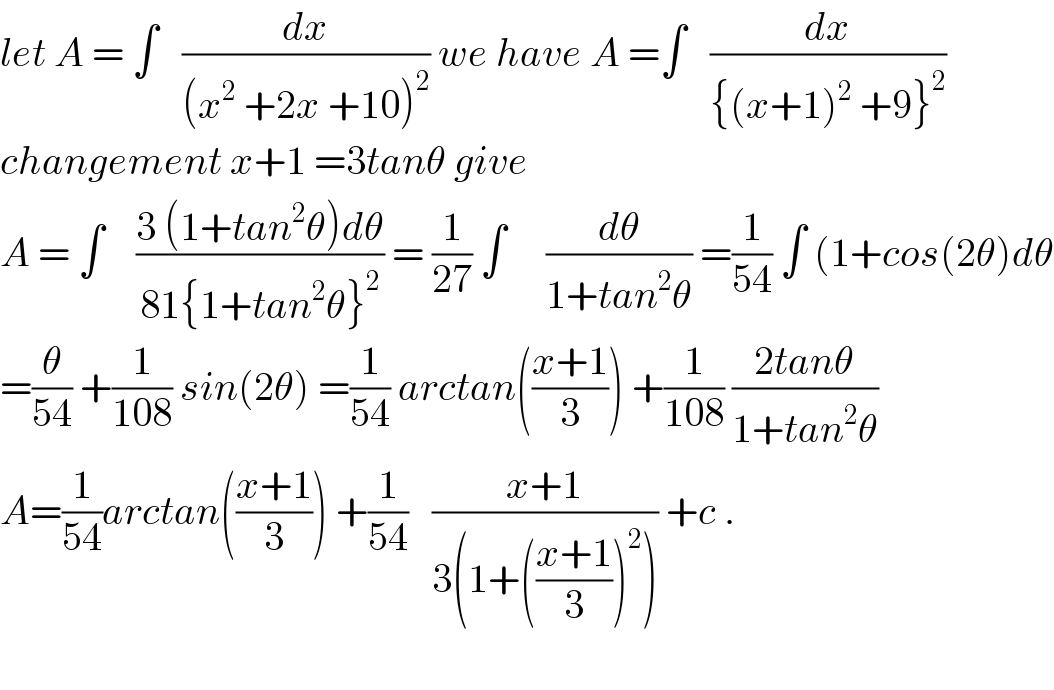
let A = ∫ (dx/((x^2 +2x +10)^2 )) we have A =∫ (dx/({(x+1)^2 +9}^2 )) changement x+1 =3tanθ give A = ∫ ((3 (1+tan^2 θ)dθ)/(81{1+tan^2 θ}^2 )) = (1/(27)) ∫ (dθ/(1+tan^2 θ)) =(1/(54)) ∫ (1+cos(2θ)dθ =(θ/(54)) +(1/(108)) sin(2θ) =(1/(54)) arctan(((x+1)/3)) +(1/(108)) ((2tanθ)/(1+tan^2 θ)) A=(1/(54))arctan(((x+1)/3)) +(1/(54)) ((x+1)/(3(1+(((x+1)/3))^2 ))) +c .
$${let}\:{A}\:=\:\int\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{10}\right)^{\mathrm{2}} }\:{we}\:{have}\:{A}\:=\int\:\:\:\frac{{dx}}{\left\{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{9}\right\}^{\mathrm{2}} } \\ $$$${changement}\:{x}+\mathrm{1}\:=\mathrm{3}{tan}\theta\:{give}\: \\ $$$${A}\:=\:\int\:\:\:\:\frac{\mathrm{3}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{81}\left\{\mathrm{1}+{tan}^{\mathrm{2}} \theta\right\}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{27}}\:\int\:\:\:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\frac{\mathrm{1}}{\mathrm{54}}\:\int\:\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right){d}\theta\right. \\ $$$$=\frac{\theta}{\mathrm{54}}\:+\frac{\mathrm{1}}{\mathrm{108}}\:{sin}\left(\mathrm{2}\theta\right)\:=\frac{\mathrm{1}}{\mathrm{54}}\:{arctan}\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)\:+\frac{\mathrm{1}}{\mathrm{108}}\:\frac{\mathrm{2}{tan}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{54}}{arctan}\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)\:+\frac{\mathrm{1}}{\mathrm{54}}\:\:\:\frac{{x}+\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \right)}\:+{c}\:. \\ $$$$ \\ $$
Answered by ajfour last updated on 13/Sep/18
∫(dx/([(x+1)^2 +3^2 ]^2 )) let x+1=3tan 𝛉 ⇒ ∫ ((3sec^2 θdθ)/(81sec^4 θ)) = (1/(54))∫2cos^2 θdθ +c .... = (1/(54))[ tan^(−1) (((x+1)/3))+((3(x+1))/((x^2 +2x+10)))]+c .
$$\:\:\int\frac{{dx}}{\left[\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right]^{\mathrm{2}} } \\ $$$${let}\:\:\boldsymbol{{x}}+\mathrm{1}=\mathrm{3tan}\:\boldsymbol{\theta} \\ $$$$\Rightarrow\:\int\:\frac{\mathrm{3sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{81sec}\:^{\mathrm{4}} \theta}\:=\:\frac{\mathrm{1}}{\mathrm{54}}\int\mathrm{2cos}\:^{\mathrm{2}} \theta{d}\theta\:+{c}\:\: \\ $$$$…. \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{54}}\left[\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{3}\left({x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)}\right]+{c}\:. \\ $$
Commented by Tinkutara last updated on 14/Sep/18
Thank you very much Sir! But in answer there is no multiplication with 3 in numerator of 2nd term.
Commented by Tinkutara last updated on 14/Sep/18
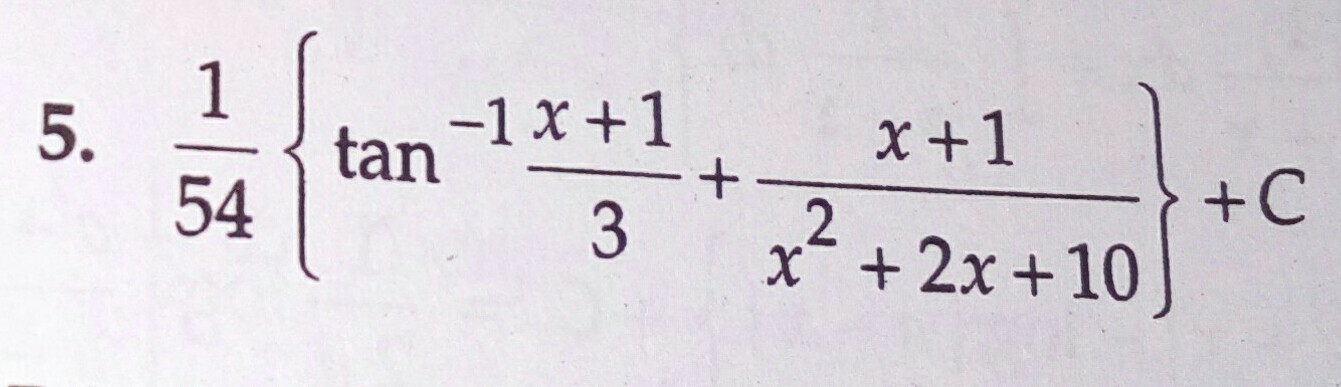
Commented by MJS last updated on 14/Sep/18
(d/dx)[(1/(54))(arctan ((x+1)/3)+((x+1)/(x^2 +2x+10))]= =(1/(54))((1/(3((((x+1)^2 )/9)+1)))+((x^2 +2x+10−(x+1)(2x+2))/((x^2 +2x+10)^2 ))) =(1/(54))((3/(x^2 +2x+10))+((−x^2 −2x+8)/((x^2 +2x+10)^2 )))= =(1/(27))×((x^2 +2x+19)/((x^2 +2x+10)^2 )) so the book is wrong
$$\frac{{d}}{{dx}}\left[\frac{\mathrm{1}}{\mathrm{54}}\left(\mathrm{arctan}\:\frac{{x}+\mathrm{1}}{\mathrm{3}}+\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right]=\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{54}}\left(\frac{\mathrm{1}}{\mathrm{3}\left(\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}}+\mathrm{1}\right)}+\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}−\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{2}\right)}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{54}}\left(\frac{\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}+\frac{−{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{8}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)^{\mathrm{2}} }\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}×\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{19}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)^{\mathrm{2}} } \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{book}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by Tinkutara last updated on 14/Sep/18
Thank you Sir!
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Sep/18
∫(dx/({(x+1)^2 +3^2 }^2 )) x+1=3tanα dx=3sec^2 αdα ∫((3sec^2 αdα)/({3^2 (1+tan^2 α)}^2 )) (1/(27))∫((sec^2 αdα)/(sec^4 α)) (1/(27))∫((1+cos2α)/2)dα (1/(54)){α+((sin2α)/2)}+c (1/(54)){tan^(−1) (((x+1)/3))+(1/2)×((2tanα)/(1+tan^2 α))} (1/(54)){tan^(−1) (((x+1)/3))+(((x+1)/3)/(1+(((x+1)/3))^2 ))}+c (1/(54)){tan^(−1) (((x+1)/3))+((3(x+1))/(x^2 +2x+10))}+c
$$\int\frac{{dx}}{\left\{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \right\}^{\mathrm{2}} } \\ $$$${x}+\mathrm{1}=\mathrm{3}{tan}\alpha \\ $$$${dx}=\mathrm{3}{sec}^{\mathrm{2}} \alpha{d}\alpha \\ $$$$\int\frac{\mathrm{3}{sec}^{\mathrm{2}} \alpha{d}\alpha}{\left\{\mathrm{3}^{\mathrm{2}} \left(\mathrm{1}+{tan}^{\mathrm{2}} \alpha\right)\right\}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{27}}\int\frac{{sec}^{\mathrm{2}} \alpha{d}\alpha}{{sec}^{\mathrm{4}} \alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{27}}\int\frac{\mathrm{1}+{cos}\mathrm{2}\alpha}{\mathrm{2}}{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{54}}\left\{\alpha+\frac{{sin}\mathrm{2}\alpha}{\mathrm{2}}\right\}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{54}}\left\{{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{tan}\alpha}{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{54}}\left\{{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+\frac{\frac{{x}+\mathrm{1}}{\mathrm{3}}}{\mathrm{1}+\left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\right\}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{54}}\left\{{tan}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{3}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}}\right\}+{c} \\ $$
Commented by Tinkutara last updated on 14/Sep/18
Thanks very much Sir! But please check the answer in book.
Answered by MJS last updated on 14/Sep/18
∫(dx/((x^2 +2x+10)^2 ))=∫(dx/(((x+1)^2 +9)^2 ))= [t=x+1 → dx=dt] =∫(dt/((t^2 +9)^2 ))= [reduction formula ∫(dt/((at^2 +b)^n ))=(t/(2b(n−1)(at^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(dt/((at^2 +b)^(n−1) ))] =(t/(18(t^2 +9)))+(1/(18))∫(dt/(t^2 +9))= ∫(dt/(t^2 +9))= [u=(t/3) → dt=3du] =(1/3)∫(du/(u^2 +1))=(1/3)arctan u=(1/3)arctan (t/3) =(t/(18(t^2 +9)))+(1/(54))arctan (t/3)= =((x+1)/(18(x^2 +2x+10)))+(1/(54))arctan ((x+1)/3) +C
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)^{\mathrm{2}} }=\int\frac{{dx}}{\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{1}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{reduction}\:\mathrm{formula}\right. \\ $$$$\left.\:\:\:\:\:\:\int\frac{{dt}}{\left({at}^{\mathrm{2}} +{b}\right)^{{n}} }=\frac{{t}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)\left({at}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }+\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)}\int\frac{{dt}}{\left({at}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }\right] \\ $$$$=\frac{{t}}{\mathrm{18}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}+\frac{\mathrm{1}}{\mathrm{18}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{9}}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{9}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\frac{{t}}{\mathrm{3}}\:\rightarrow\:{dt}=\mathrm{3}{du}\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:{u}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\frac{{t}}{\mathrm{3}} \\ $$$$ \\ $$$$=\frac{{t}}{\mathrm{18}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}+\frac{\mathrm{1}}{\mathrm{54}}\mathrm{arctan}\:\frac{{t}}{\mathrm{3}}= \\ $$$$=\frac{{x}+\mathrm{1}}{\mathrm{18}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)}+\frac{\mathrm{1}}{\mathrm{54}}\mathrm{arctan}\:\frac{{x}+\mathrm{1}}{\mathrm{3}}\:+{C} \\ $$
Commented by Tinkutara last updated on 14/Sep/18
Thanks very much.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *